§ 10. Лінійні програми

Лінійні алгоритми і відповідні їм програми складаються з команд присвоєння, введення-виведення даних та викликів процедур.

1. Команда присвоєння. Команду присвоєння використовують для надання початкового значення змінній або для зміни її поточ­ного значення. Команда присвоєння має такий загальний вигляд:

<А> = <В>

Тут А — назва змінної, В — вираз, «=» — символ присвоєння.

Вираз може складатись зі сталих, змінних, назв функцій, які з’єднані символами операцій.

Дія команди. Обчислюється значення виразу В і результат при­своюється змінній А. Попереднє значення змінної А втрачається.

Розглянемо чотири команди присвоєння:

а = 5:b=10:с = -2.6

d = (а + b) / (b - а) + с.

Яке значення буде присвоєне змінній d? Переконайтесь, що 0,4.

Коментуючи наведений вище фрагмент коду, не можна говори­ти: «а дорівнює 5, b дорівнює 10 і т.д.». Правильно висловлюватись так: «змінній а присвоїти значення 5, змінній b надати 10 і т.д.».

Зауваження. Якщо числовий тип змінної А в команді присвоєн­ня не відповідає числовому типу виразу В, то після обчислення виразу результат автоматично буде перетворений до типу змінної А. Наприклад, якщо під час обчислення деякого виразу В отримано число 12.45, а змінна А описана як ціла, то результат буде такий: А= 12 (число заокруглиться до найближчого цілого).

2. Обмін значеннями між змінними. Розглянемо, як можуть дві змінні обмінятися значеннями. Обмін значеннями між двома змін­ними виконують за допомогою третьої допоміжної змінної. Нехай а та b — назви змінних, які обмінюються значеннями. Використаємо допоміжну (додаткову) змінну, яку назвемо с.

Нехай виконались команди а = 5 : b = 7. Обмін значеннями між змінними а і b можна здійснити за допомогою такого алгоритму:

с = а 'змінна с набула значення 5

a = b 'змінна а набула значення 7

b = с 'змінна b набула значення 5

Чому не можна цю задачу розв’язати так: a = b : b = а? Переко­найтеся, що тоді обидві змінні отримають значення 7 і обмін не від­будеться.

3. Арифметичні вирази. Арифметичні вирази призначені для описування дій з числовими даними. Вони дають змогу за допомо­гою позначень, близьких до математичних, закодувати формули. Результатом обчислення арифметичного виразу є число.

Арифметичні вирази будує користувач, комбінуючи сталі, змін­ні, функції і поєднуючи їх за допомогою символів операцій.

Над числовими даними можна виконати такі операції:

10. піднесення до степеня (^);

11. множення (*) та ділення (/);

12. додавання (+) та віднімання (-).

Послідовність виконання операцій у виразах така ж, як у мате­матиці. Її описують правилом пріоритетів (порядком виконання операцій). Наведемо цей порядок за спаданням:

1. обчислюються значення аргументів і значення функцій (якщо вони є у виразі);

2. виконуються всі наявні операції піднесення до степеня;

3. виконується операція присвоєння знаку;

4. виконуються операції множення та ділення;

5. виконуються операції додавання та віднімання.

*Переконайтеся, що вирази -2 – 3 * -4 чи 3 * —4 – 2 дають 10.

Операції одного рівня виконуються послідовно зліва направо.

Для зміни послідовності виконання операцій використовують круг­лі дужки. Кількість відкритих і закритих дужок повинна бути од­наковою. Спочатку обчислюються вирази у дужках. Якщо є вкла­дені дужки, то спочатку обчислюються вирази у внутрішніх дуж­ках, а потім — у зовнішніх та н..

Оформлення виразів. Вирази записують в одному або у кількох рядках. Символом переносу є «_». Символи арифметичних операцій у випадку переносу дублювати не можна.

Правило лінійного запису виразів: показник степеня, індекси, чисельники та знаменники розміщують у горизонтальному рядку (у лінію). Потрібно уважно записувати знаменники. У багатьох випад­ках їх беруть у дужки. Зазначимо, що зайва пара дужок у складно­му виразі до помилки не призводить.

4. Стандартні математичні функції. Функції поділяють на стан­дартні та нестандартні. Аргумент функції завжди беруть у круглі дуж­ки. Аргументом може бути стала, змінна, арифметичний вираз, інша стандартна функція. Основні стандартні функції наведені в табл. 1.6.

Таблиця 1.6. Стандартні функції

Функція в VB	Функція в VBA	Математич­ний запис	Коментар
Sin(X)	Sin(X)	sin x	x задають у радіанах
Cos(X)	Cos(X)	cos x	х задають у радіанах
Tan(X)	Tan(X)	tg x	х задають у радіанах
Atan(X)	Atn(X)	arctg x	Арктангенс х
Abs(X)	Abs(X)	|x|	Модуль x
Sqrt(X)	Sqr(X)		Квадратний корінь х
Log(X)	Log(X)	ln x	Логарифм натуральний х
Exp(X)	Exp(X)	ex	Експонента
Floor()	Int(X)	[x]	Заокруглення числа до цілого, яке є не більше від x
Стор. 146	Rnd(X)		Випадкове число з проміжку [0;1)

У середовищі VB математичні функції записують, зазначаючи cлово Math з крапкою перед функцією, наприклад, Math.sin(). Це оз­начає, що у VB математичні функції є компонентами класу Math. Про інші функції можна дізнатися, набравши в тексті коду слово Math з крапкою — отримаєте вікно з усіма функціями класу Math. Розглянемо приклади значень деяких функцій у двох середовищах.

VB	VBA	Значення
Math.Tan(O)	Tan(0)	0
Math.Abs(-4)	Abs(-4)	4
Math.Sqrt(2 * 2 + 5)	Sqr(2 * 2 + 5)	3
Math. Floor (2.5)	Int(2.5)	2
Math. Floor (-2.5)	Int(—2.5)	-3

5. Друга задача про трикутник. Розглянемо задачу, під час роз­в’язування якої використаємо стандартну функцію і навчимося пра­вильно записувати вирази.

Задача 1. Написати програму для обчислення площі трикутника за відомими трьома сторонами а, b, с, де а = 5; b = 3,6; с = 4,2.

Розв’язування. Периметр і площу трикутника зберігатимемо у змінних pis. Для обчислення площі застосуємо формулу Герона.

‘ Про трикутник

Dim a As Single, b As Single, с As Single

a = 5 : b = 3.6 : c = 4.2

Dim p As Single, s As Single

p = a + b + c : p = p/ 2

s = Math.Sqrt(p * (p - a) * (p - b) * (p - c)) 'Це для VB

s = Sqr(p * (p - a) * (p - b) * (p - c)) 'Це для VBA

<вивести s>

Завдання 1. Реалізуйте проект розв’язування задачі 1.

Завдання 2. Виконайте програму, якщо a=8,2; b=6,3; c=9,1.

Завдання 3. Модифікуйте код так: обчисліть висоту трикутника, опущену на сторону a.

6. Дві нові операції \ та Mod, або як обчислити суму цифр у числі. З цілими даними можна виконати ще дві операції:

• обчислення цілої частини від ділення (символ операції \);

• обчислення остачі від ділення двох чисел (операція Mod).

Перша операція відкидає дробову частину результату, наприклад, 5\2=2, 359\100=3, а друга – обчислює остачу: 5 Mod 2=1, 17 Mod 3=2.

Задача 2. Дано тризначне ціле число А. Обчислити суму його цифр.

Розв’язування. Позначимо шукані цифри с1, с2, с3, а суму – s. Розглянемо будь-яке тризначне число, наприклад 357, і переконаємося, що наступна програма обчислює суму (15) його цифр:

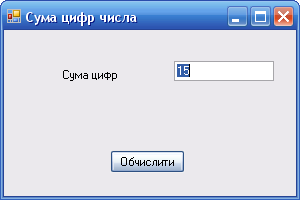' Сума цифр числа

Dim а, с1, с2, с3, s As Integer 'Це для VB

а = 357

с1 = а \ 100 'отримаємо 3

с2 = а \ 10 Mod 10 'отримаємо 5

с3 = a Mod 10 'отримаємо 7

s = с1 + с2 + с3

<вивести s>

Завдання. Реалізуйте проект розв’язування задачі 2.