Лекция №3

Тема «Простейшие узлы вычислительной техники»

1. ЛОГИЧЕСКИЕ ФУНКЦИИ.

   1. Понятие о логической функции и логическом устройстве.

   2. Диодно-резисторные схемы.

2. ТРИГГЕРЫ.

   1. Классификация триггеров.

   2. Асинхронные триггеры.

   3. Синхронные триггеры.

   4. Д-триггеры и Т-триггеры.

   5. JK-триггеры

3. РЕГИСТРЫ.

   1. Параллельный регистр.

   2. Сдвиговый регистр.

   3. Последовательный регистр.

1. ЛОГИЧЕСКИЕ ФУНКЦИИ

1.1. Понятие о логической функции и логическом устройстве

Для обозначение различных предметов, понятий, действий пользуются словами. Слова строятся из букв, которые берутся из некоторого набора их, называемого алфавитом.

В цифровой технике для тех же целей пользуются кодовые слова. Особенность этих слов состоит в том, что все они имеют одинаковую длину (т.е. представляют собой последовательность букв одинаковой длины) и для их построения используется простейший алфавит, состоящий лишь из двух букв. Эти буквы принято обозначать символами 0 и 1.  Таким образом, кодовое слово в цифровой техники есть последовательность символов 0 и 1 определенной длины, например 10111011. Такими словами могут представляться и числа, в этом случае 0 и 1 совпадают по смыслу с обычными арабскими цифрами. При представлении кодовым словом некоторой нечисловой информации, чтобы отличать буквы 0 и 1 от цифр, будем эти буквы называть соответственно логическим нулем и логической единицей.

Если длина кодовых слов составляет n разрядов, то можно построить 2ⁿ различных комбинаций - кодовых слов. Например при n=3 можно построить 2³=8 слов: 000, 001, 010, 011, 100, 101, 110, 111.

Информация, которая передается между отдельными узлами (блоками) сложного цифрового устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Для того, чтобы подчеркнуть особенности таких функций, состоящую в том, что сама функция и ее аргументы могут принимать значения логического нуля и логической единицы, будем эти функции называть функциями алгебры логики (ФАЛ).

Устройства, предназначенные для формирования функций алгебры логики, в дальнейшем будем называть логическими устройствами или цифровыми устройствами.

Цифровые устройства (либо их узлы) можно делить на типы по различным признакам.

По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.

На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно, символ за символом (в так называемой последовательной форме). Пример такого устройства показан на рисунке 3.1,а.

На входы устройства параллельного действия все n символов каждого входного кодового слова подаются одновременно (в так называемый параллельной форме). В такой же форме образуется на выходе выходное слово. Очевидно, при параллельной форме приема и передачи кодовых слов в устройстве необходимо иметь для каждого разряда входного (выходного) слова отдельный вход (выход).

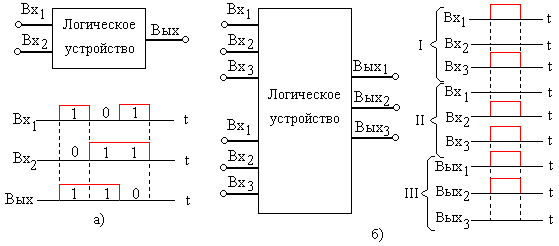
Рис.3.1. Пример устройства последовательного (а) и параллельного действия(б)

Пример такого устройства показан 3.1,б. Устройство выполняет над разрядами входных слов ту же логическую операцию (выявляя несовпадение символов соответствующих разрядов входных слов), что и устройство, показанное на рисунке 3.1,а, но в параллельной форме. Входы устройства разделены на две группы (I и  II), каждая из которых предназначена для приема трехразрядного входного кодового слова в параллельной форме. На выходах устройства также в параллельной форме получается трехразрядное выходное слово.

В устройствах смешанного действия входные и выходные кодовые слова представляются в разных формах. Например, входные слова - в последовательной форме, выходные - в параллельной. Устройства смешанного действия могут использоваться для преобразования кодовых слов из одной формы представления в другую (из последовательной формы в параллельную и наоборот).

По способу функционирования логические устройства (и их схемы) делятся на два класса: комбинационные устройства (и соответственно комбинационные схемы) и последовательностные устройства (последовательностные схемы).

В комбинационном устройстве (называемом также автоматом без памяти) каждый символ на выходе (логический 0 или логическая 1) определяются лишь символами (лог. 0 или лог. 1), действующими в данный момент времени на входах устройства, и не зависит от того, какие символы ранее действовали на этих входах. В этом смысле комбинационные устройства лишены памяти (они не хранят сведений о прошлом работы устройства).

В последовательностных устройствах (или автоматах с памятью) выходной сигнал определяется не только набором символов, действующих на входах в данный момент времени, но и внутренним состоянием устройства, а последнее зависит от того, какие наборы символов действовали во все предшествующие моменты времени. Поэтому можно говорить, что последовательностные устройства обладают памятью (они хранят сведения о прошлом работы устройства).

Рассмотрим примеры работы комбинационного и последовательностного устройств.

Пусть устройство (рис. 3.2,а) предназначено для формирования на выходе сигнала, определяющего совпадение сигналов на входах: на выходе формируется логическая 1 в случаях, когда на обоих входах действует логическая 1, либо на обоих входах действует логический 0; если на одном из входов действует лог. 1, а на другом - лог. 0, то на выходе устройства образуется лог. 0. Такое устройство является комбинационным, в котором значение формируемой на выходе логической функции определяется лишь значениями ее аргументов в данный момент времени.

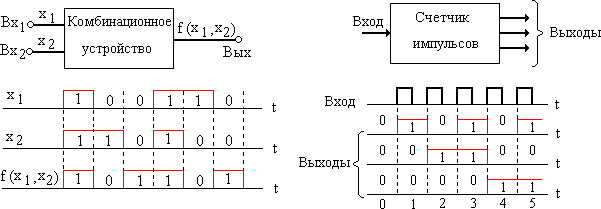
Рис.3.2. Примеры работы комбинационного (а) и последовательностного устройств (а )

Рассмотрим другой пример. Счетчик на рисунке 3.2,б подсчитывает импульсы. В каждый момент времени его состояние соответствует числу поступивших на вход импульсов. Выходная информация определяется тем, каково было состояние счетчика до данного интервал времени и поступает или нет на вход импульс в этом интервале времени. Таким образом, данное устройство является последовательностным устройством.

1.2.Диодно-резисторные схемы

Сформулируем некоторые начальные условия:

а) электрическое сопротивление линий связи в схемах принимается равным нулю, вследствие чего падение напряжения на них всегда имеет нулевое значение независимо от величины протекающего по ним тока;

б) сопротивление диода принимается равным нулю, если он включен в проводящем направлении. Если же диод заперт (не проводит), то сопротивление его бесконечно велико и ток через него не протекает;

в) вольтметр, подключенный к каким-либо точкам схемы, состояние ее не меняет, поскольку предполагается, что вольтметр имеет бесконечно большое входное сопротивление.

Логические элементы

В названии «комбинационная схема» отражен тот факт, что выходной сигнал логической структуры полностью определяется комбинацией входных двоичных сигналов. Это значит, что в самой структуре нет никаких запоминающих элементов, которые могли бы привести к различной реакции логической схемы на одни и те же комбинации входных сигналов. В современных устройствах дискретного действия используется большой набор логических элементов. Однако основными из них являются только три: схема И, схема ИЛИ, схема НЕ (инвертор). Все остальные логические схемы представляют собой различные комбинации этих трех элементов. Из них может быть построен любой комбинационный преобразователь двоичных кодов.

Элемент И

Обратимся к рис. 3.3. На нем изображено: источник питания U, два переключателя А и В, два резистора R1 и R2, два диода V1 и V2. Пунктиром обведен логический элемент И, имеющий два входа 1 и 2 и один выход. Переключатели А и В предназначены для подачи двоичных сигналов на входы схемы И. Переключатели выполняют двойную функцию. Во-первых, они используются как запоминающие элементы, т. е. моделируют двоичные логические аргументы. Во-вторых, подают на входы элемента И напряжение, равное нулю либо равное U. Условимся считать, что если А = 0, то на вход схемы И подается нулевой (низкий) уровень напряжения. Если же А = 1, то подается единичный (высокий) уровень. И наоборот, если напряжение равно нулю, то аргумент А имеет нулевое значение. Если же напряжение принимает значение высокого уровня, то А = 1. Эта интерпретация сохраняется и в случае любых других логических элементов, рассматриваемых в данной книге.

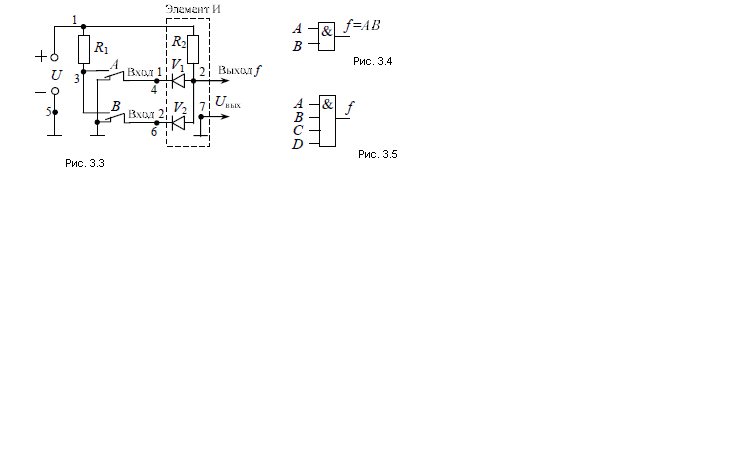
Рис.3.3, 3.4, 3.5

На рис. 1 переключатели изображены в нулевом состоянии. Это значит, что А = В = 0, то есть на входы элемента И поданы низкие уровни напряжения. Поскольку диоды находятся в проводящем состоянии, то падение напряжения на них равно нулю. Следовательно, Uвых также равно нулю. Таким образом, если А = В = 0, то Uвых = 0. Если Uвых = 0, то говорят: схема заперта. Пусть В = 1. Тогда на вход 2 поступит высокий уровень, равный напряжению источника U. Выходное напряжение останется равным нулю, так как диод V1 проводит. Переключатель А переведем в единичное положение, а В – в нулевое. Выходное напряжение по-прежнему будет равно нулю, так как через диод V2 протекает ток. Переведем в единичное положение оба переключателя, то есть примем А = В = 1. Выходное напряжение будет равно U. В этом случае говорят: схема открыта. Буквой f на рис. 1 обозначен выход схемы И. Это функция, зависящая от значений входных сигналов. Как логическая переменная, она может принимать два значения: 0 и 1. Условимся считать, что ее нулевому значению соответствует низкий уровень напряжения, а единичному – высокий. В табл. 1 для каждого набора значений аргументов указаны логические значения выходного сигнала (колонка f ). В колонке Uвых даны значения выходного напряжения. По таблице видно, что элемент И реализует операцию конъюнкции. Логический элемент И принято обозначать так, как показано на рис. 3.3. Буквы А и В обозначают входные сигналы, f – выходной сигнал элемента И. Мы рассмотрели элемент И с двумя входами. В общем случае число входов может быть любым. Например,на рис. 3 изображен логический элемент с четырьмя входами, реализующий конъюнкцию вида f = ABCD.

Элемент ИЛИ

Обратимся к рис. 3.6, на котором приведена логическая схема ИЛИ с двумя входами. Переключатели изображены в нулевом положении, т. е. А = В = 0. По схеме видно, что при этом и f = 0. Переведем в единичное положение переключатель В Тогда диод V2 окажется в проводящем состоянии. Если R2 >> R1, то выходное напряжение практически равно U, что соответствует высокому уровню напряжения и, следовательно, f = 1.

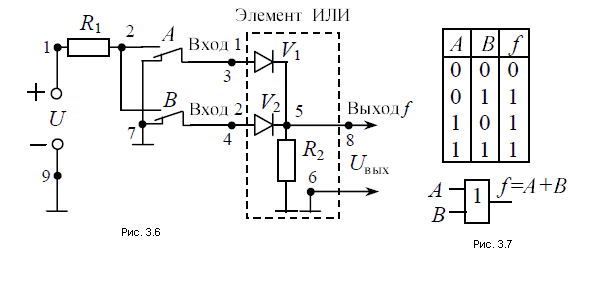
Рис.3.6, 3.7

Вернем переключатель В в нулевое положение, а переключатель А переведем в единичное. Очевидно, что и в этом случае f = 1. Если в единичное положение перевести оба переключателя, то по-прежнему выходное напряжение будет иметь высокий уровень.

В табл. 3.2 каждому из четырех наборов значений аргументов поставлено в соответствие состояние выхода элемента ИЛИ. По таблице видно, что схема ИЛИ реализует логическую операцию дизъюнкции.

Двухвходовую схему ИЛИ принято обозначать так, как показано на рис. 3.6. В общем случае схема ИЛИ, как и логический элемент И, может иметь любое число входов.

Инвертор и схема И-НЕ

Принципиальная схема инвертора – логического элемента НЕ – приведена на рис. 3.8(обведена пунктирным контуром). По схеме видно, что при А = 0 (как изображено на рис. 3.7) ток через базу не протекает и транзистор заперт. Следовательно, выходное напряжение Uвых = U, т. е. при А = 0 имеем f = 1.

Переведем переключатель А в единичное положение, т. е. примем А = 1. Ток, протекающий от источника U через токоограничивающий резистор R1 и базу, поддерживает транзистор в открытом (проводящем) состоянии. Падение напряжения на открытом транзисторе можно считать равным нулю. Следовательно, f = 0, если А = 1. Таким образом, инвертор реализует булеву функцию f = А

На рис. 3.8,а показано обозначение инвертора. Очевидно, что инвертор может быть только одновходовым элементом. Из более сложных логических схем рассмотрим элемент И-НЕ ( рис.3.8).

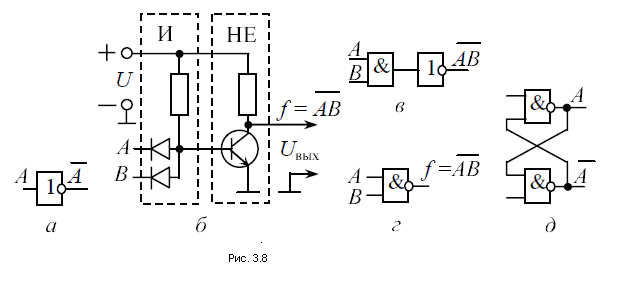
Рис.3.8а,б,г,д

Буквами А и В обозначены входы (входные сигналы) элемента И. Выход элемента И подключен к входу инвертора. В результате получился элемент, реализующий булеву функцию f = АВ . Эту схему называют элементом Шеффера. На рис. 3.8,в изображена та же схема И-НЕ с использованием условных обозначений элементов И и НЕ, а на рис. 3.8,г – в виде одного элемента И-НЕ. На схемах И-НЕ можно построить электронный запоминающий элемент – триггер (рис. 3.8,д), имеющий два устойчивых состояния, условно названных нулевое и единичное.

Триггеры, как и двухпозиционные переключатели, используются в комбинационных схемах для физического моделирования логических аргументов, в связи с чем все переключатели на рис. 3.2, 3.5, 3.7 можно заменить триггерами. Для комбинационных схем триггер не является основным элементом, так как его роль сводится лишь к хранению значений логических аргументов, поэтому в данном разделе триггеры не рассматриваются. Вся информация о триггерах, наиболее важная с логической точки зрения, приведена в разделе, посвященном многотактным схемам, в которых триггерам отводится ведущая роль.