5.2 Метод исправленного крюйс-пеленга.

Этот метод, является частным случаем применения сопутствующей линии положения (СЛП). В принципе, этот подход возможен и для других типов изолиний или линий положения, например дистанции (крюйс-дистанция), но изолиния пеленга имеет самую простую форму и наглядность, поэтому остановимся именно на нём.

Этим методом, с достаточной точностью, можно определить все параметры движения судна (скорость, курс) и новое (или предыдущее) место судна, которое можно считать обсервованным.

Для определения этих параметров, необходимо знать – пеленг на маяк, обсервованное место судна, и дополнительная изолиния, причём последовательность получения этих параметров не важна. Условием использование метода, есть постоянство курса и скорости судна.

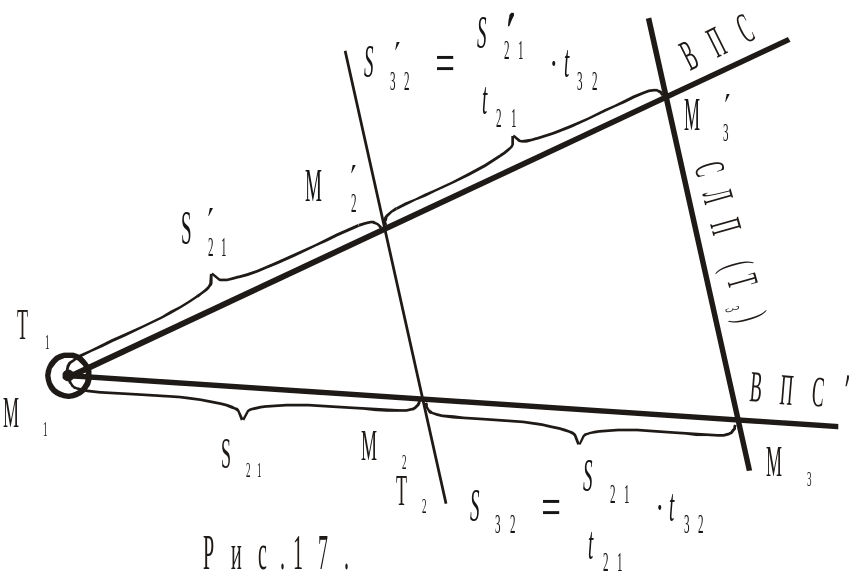
Риса. 5.3 Получение СЛП

Предположим, что судно движется с постоянной скоростью и курсом, точное значение которых несущественно. В один из моментов времени Т₁ получено точ

ное (обсервованное) место судна М₁, следовательно, возможный путь судна (ВПС), можно проложить через эту точку.

В другой момент времени Т₂, взят пеленг на маяк или получена какая-либо ЛП. За этот промежуток времени t₂₁, судно, если бы действительно следовало этим курсом, пришло бы в точку М₁ и прошло бы расстояние S₂₁, предполагаемая скорость судна при этом была бы:

Очевидно, что в момент времени T₃ за некоторый другой промежуток времени t₃₂, следуя этой скоростью, судно вдоль ВПС прошло бы расстояние:

и попало бы в точку М₃.

Теперь через эту же точку проведём другой ВПС', понятно, что в момент времени Т₂, судно бы оказалось в точке М'₂ и прошло бы расстояние S'₂₁, предполагаемая скорость при этом была бы:

,

и за промежуток времени t₃₂, следуя этой скоростью, судно вдоль ВПС' прошло бы расстояние:

и попало бы в точку М'₃.

Проведя через точки М₃ и М'₃ линию, мы увидим, что она параллельна сделанному пеленгу или ЛП, следовательно, можно сделать вывод, что на этой линии лежат все возможные места судна на момент T₃ и, разумеется, истинное место.

Особенностью этой линии является то, что она перемещается вместе с судном, сопутствует ему, потому и названа – сопутствующей линией положения СЛП.

Если в момент T₃ сделать наблюдение некоторой другой изолинии, например изобаты, то на пересечении с СЛП мы получим другое обсервованное место судна и через обе обсервованные точки, можем провести истинную линию пути судна, из которой можем получить скорость и курс.

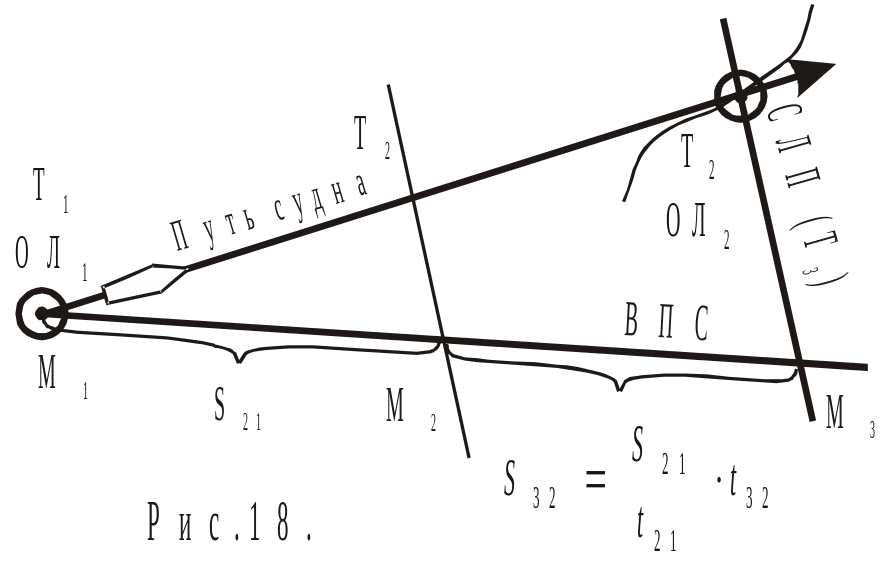
Рис. 5.4 и 5.5 Получение пути судна с помощью СЛП

СЛП можно переносить не только вперёд по ходу судна, но и назад, на какую либо изолинию полученную ранее, например изостадию и получить место и все остальные параметры движения ранее полученной обсервации в момент времени Т₀. Более того, построение полностью обратимо, то есть вначале можно измерить изолинию, потом снять пеленг и напоследок произвести обсервацию, затем на момент получения изолинии определить обсервованное место.

5.3 Общий случай слп.

Предположим, что получены три разновременные линии положения не пересекающихся в одной точке.

Судно двигаясь с постоянной скоростью и курсом, поочерёдно пересекает все три линии ЛП_I, ЛП_II и ЛП_III в моменты времени Т₁, Т₂ и Т₃. Наша задача найти геометрическое место точек в которых может находиться судно в момент времени Т₄. Можно доказать, что эти точки будут лежать на одной прямой, то есть нам достаточно получить, как минимум, две точки для её построения. Эта линия и будет СЛП(Т₄).

В момент времени Т₁ судно могло находиться в любой точке ЛП_I и следовать любым курсом (нам не важно каким), одним из возможных курсов может быть курс вдоль ЛП_I. Следуя этим курсом, судно в момент Т₂ пересечёт ЛП_II, а в момент Т₃ ЛП_III, обозначим это расстояние – S₃₂, рассчитаем скорость на этом промежутке, за время t₃₂ = T₃ – T₂:

.

Двигаясь с этой скоростью дальше к моменту времени Т₄, судно прошло бы расстояние и оказалось бы в точке М₄₁, лежащей на СЛП(Т₄).

Аналогичные рассуждения можно провести и для ЛП_II, и для ЛП_III и получить точки М₄₂, М₄₃, лежащие на СЛП(4). Если все три точки оказались на одной прямой, значит, наши построения верны.

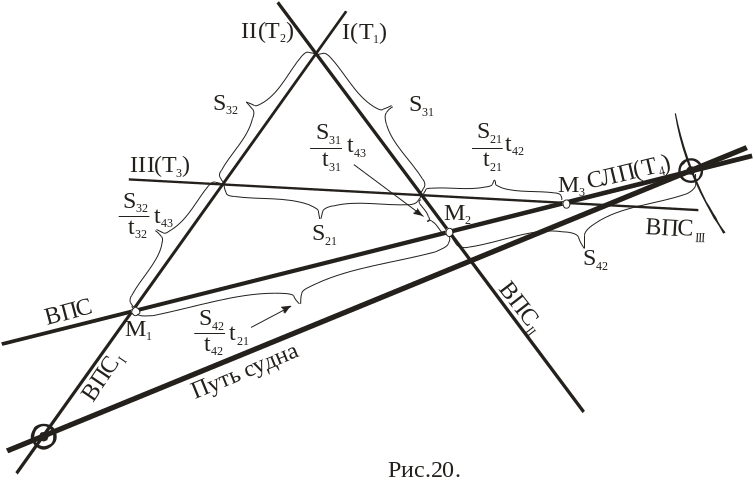
Рис. 5.6 Построение СЛП в общем случае

Если в момент времени Т₄, наблюдалась какая либо изолиния или ЛП, мы получим обсервованное место судна на это время, а применив рассуждения приведенные в 8.1, мы можем получить место судна в момент Т₁, таким образом, зная две обсервованные точки, мы легко рассчитаем скорость и курс судна. В этом построении СЛП(Т₄), поочерёдно пересекая все ЛП, вполне удовлетворяет всем требованиям возможного пути судна (ВПС).