Раздел 5 использование разновременных лп

5.1 Общий случай решения основной задачи судовождения

Практически все измерения навигационных параметров, которые выполняются для ОМС одним наблюдателем, всегда бывают разновременными. Условно все измерения, выполненные одним наблюдателем в быстрой последовательности считаются одновременными.

При движении судна разновременные измерения выполняются в различных точках и должн6ы быть приведены к одному моменту и месту судна. Однако такое приведение осуществляется переносом изолиний или линий положения е нужному моменту и месту судна лишь по счислению. Неточности счисления при значительных интервалах между измерениями существенно снижает точность переносимых линий и, естественно приводит к снижению точности ОМС.

Указанное выше снижение точности обсерваций при обычных крюйс-методах, заставляло судоводителей искать методы ОМС по разновременным измерениям, которые дают место судна независимое от ошибок счисления. Частные случаи такого решения задач под названием исправленного и двойного крюйс-пеленга давно и успешно применялись на флоте. Решение задачи в общем виде было предложено академиком А.Н. Крыловым и впервые с достаточным теоретическим обоснованием приведено в [10. –С. 509 - 539]. Как это так и другие навигационные пособия [1],[3],8] рассматривают общее решение задачи очень усложненно или чрезвычайно упрощенно. Наиболее полно и просто решение задачи для любых условий измерений приведено в [7], где по методике М.Н. Андреева показано решение основной задачи судовождения с помощью сопутствующих линий положения (СЛП).

Основной задачей судовождения является не только ОМС, но также определение элементов движения судна , о чем говорилось в первом разделе данного конспекта. Иными словами, в наиболее общем виде основною задачей судовож

дения является определение места судна, направления и скорости его перемещения по земной поверхности.

Уравнение равномерного и прямолинейного движения судна в прямоугольной системе координат  и  при известных скорости  и интервале времени t запишется так:

=_о+_t =_о+_•t , (5.1)

где _ та _{ -} проекции вектора движения судна на координатные оси за промежуток времени t.

Рис.5.1 Движение судна в прямоугольной системе координат

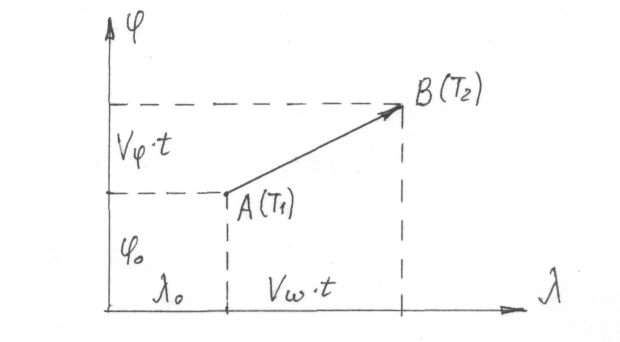
По уравнению (5.1) видно что для решения задачи необходимо знать четыре величины: координаты начала движения величину и направление вектора движения судна или его проекции на координатные оси. Для решения необходимо как минимум четыре уравнения. В общем случае это могут быть уравнения четырех изолиний с параметрами U₁, U₂, U₃ ,U₄,, которые должны быть разновременными. Они имеют вид:

U₁=f₁(₁, ₁

U₂=f₂(₂, ₂

U₃=f₃(₃, ₃

U₄=f₄(₄, ₄

Выразив текущие координаты через начальные и их приращения на протяжении интервала t, получим уравнения изолиний:

U₁=f₁(₀, ₀)

U₂=f₂(₀+_t₂₁; ₀+_t₂₁)

U₃=f₃(₀+_t₃₁; ₀+_t₃₁)

U₄=f₄(₀+_t₄₁; ₀+_t₄₁),

Где t₂₁=T₂-T₁, t₃₁=T₃-T₁; t₄₁=T₄-t₁

Решения этих уравнений относительно неизвестных величин в общем виде приведет к уравнениям:

__(U₁, U₂, U₃, U₄, t₂₁, t₃₁, t₄₁)=K₁

_₂(U₁, U₂, U₃, U₄, t₂₁, t₃₁, t₄₁)=K₂

_₃(U₁, U₂, U₃, U₄, t₂₁, t₃₁, t₄₁)=К₃ (5.2)

_₄(U₁, U₂, U₃, U₄, t₂₁, t₃₁, t₄₁)=K₄

Текущие координаты места судна на любой момент времени с учетом уравнений (5.1) прнимают вид:

__t

₂₄t

Непосредственное решение уравнений (5.2) при достаточно сложных функциональных зависимостях f₁, f₂, f₃, f₄ , а также и уравнений изолиний, представля

ет трудную задачу даже при использовании вычислительной техники. Геометрический смысл определения линии равномерного и прямолинейного движения судна, деленного на отрезки пропорциональные интервалам времени t₂₁, t₃₁, t₄₁ Показаны ниже.

Рис. 5.2 Графическое решение основной задачи судовождения

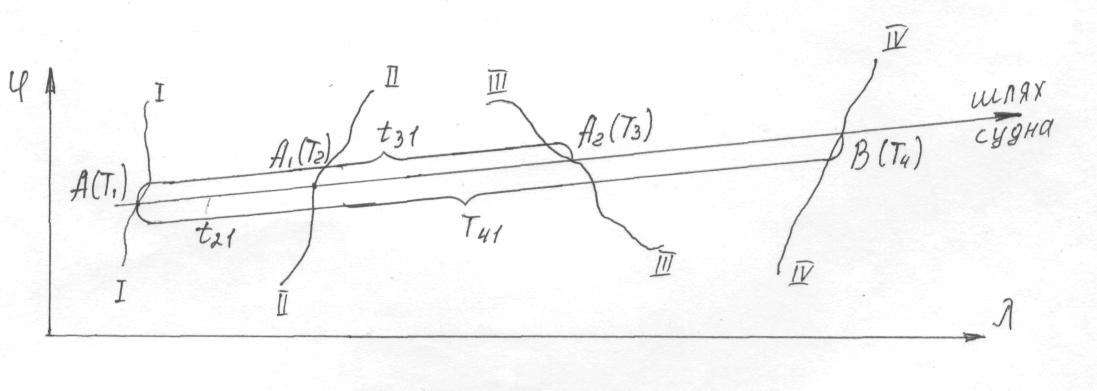
Графоаналитическое решение основной задачи судовождения разработанное до практического применения в условиях ходового мостика пока что только для условий равномерного прямолинейного движения судна. Исследования по теоретическому и практическому обоснованию решения основной задачи судовождения при неравномерному и криволинейному движении судна ожидают своих авторов.