4.4 Графические методы отыскание вероятнейшего места судна при избыточном числе линий положения.

При ОМС по двум ЛП или изолиниям имеет место существенный недостаток, а именно, практически отсутствует возможность проверить наличие систематических ошибок или промахов в измерениях и избавиться от их влияния. Частично эту проблему можно решить, получив избыточное число навигационных параметров, как правило, три или четыре.

Получив три ЛП (изолинии) и нанеся их на карту, вследствие влияния случайных и систематических погрешностей, линии положения сойдуться не в одной точке, а мы получим треугольник погрешностей. К сожалению вычесление промахов, кроме очень крупных практически невозможно, но от воздействия одинаковых систематических ошибок избавиться возможно.

Практически встают следующие вопросы:

• Каким образом лучше выбирать ориентиры?

• Где выбрать обсервованное место судна при равноточных и неравноточных измерениях?

• Как оценить точность полученного места и получить площадь, где находится место судна с наибольшей вероятностью.

4.4.1 Действие систематических ошибок.

В теоретическом курсе показывается, что если между двумя ЛП положения провести биссектрису угла, то полученная «разностная» линия будет свободна от действия систематических ошибок. Для построения достаточно двух биссектрис. Эту операцию иногда называют «разгоном» треугольника погрешностей.

Для построения биссектрис именно тех углов, при вершинах треугольника перпендикулярно линиям положения, наносятся стрелочки в направлении азимута, затем проводится биссектриса меньшего угла между стрелочками (Рис. 10).

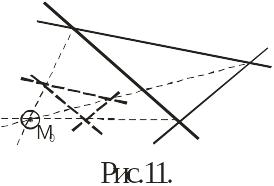
Другой способ разгона треугольника погрешностей заключается в смещении всех ЛП (или изолиний) на одну и ту же величину, в одном направлении. Далее сходные углы соединяются линиями. На пересечении этих линий мы получим место свободное от систематических погрешностей (рис.11).

При построении биссектрис и определении обсервованного места может встретиться два случая:

Ориентиры расположены в одной половине горизонта, в этом случае точка пересечения биссектрис будет лежать вне треугольника погрешностей (Рис.10 а).

Вследствие того, что в реальных условиях на систематические ошибки накладываются ещё и случайные, приём может привести к грубым ошибкам в обсервованном месте, и его следует применять с большой осторожностью.

Ориентиры расположены в разных частях горизонта. В этом случае точка пересечения биссектрис будет лежать внутри треугольника ошибок(Рис.10 б).

Учитывая то, что внутри треугольника отклонение обсервованной точки от реальной значительно меньше, чем может быть снаружи, для обсервации рекомендуется подбирать ориентиры лежащие в разных частях горизонта.

Следует помнить, что вышесказанное справедливо, лишь при допущении, что действие случайных ошибок равно нулю. Поэтому нельзя считать, что наши построения обнаруживают систематическую ошибку, скорее наоборот, они сами являются следствием предположения, что действуют только равные систематические ошибки.

4.4.2 Действие случайных ошибок.

С лучайные ошибки возникают из-за влияния разнородных факторов, учёт которых невозможен.

В случае если все линии равноточные, а действие систематических ошибок равно нулю, вероятнейшее место будет находиться на пересечении ан

тимедиан треугольника, которая представляет собой зеркальное изображение медианы относительно биссектрисы.

При увеличении треугольника в длину, обсервованное место смещается к более короткой стороне и прямому углу, что соответствует выводам из теории ошибок (чем ближе угол пересечения двух линий положения к 90, тем вес этой точки больше).