4.2 Графоаналитический метод.

Основан на обобщённом методе линий положения (ЛП). Суть способа состоит в том, что прямую, касательную к этой изолинии. Впервые этот метод был применён для определения места судна по на коротком отрезке, изолинию сколь угодно сложной формы можно заменить наблюдениям светил и проще его пояснить именно на этом примере.

Предположим, что наблюдатель находится в точке М с координатами  и , которые ему не известны и которые предстоит определить с достаточной точностью. В этой точке он измеряет высоту h светила С.

Зная высоту светила можно провести круг равных высот с радиусом z = 90 - h. Разумеется, точка М будет находиться где-то на этой окружности.

П ри этом наблюдателю известны счислимые (приблизительные) координаты _С и _С точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:

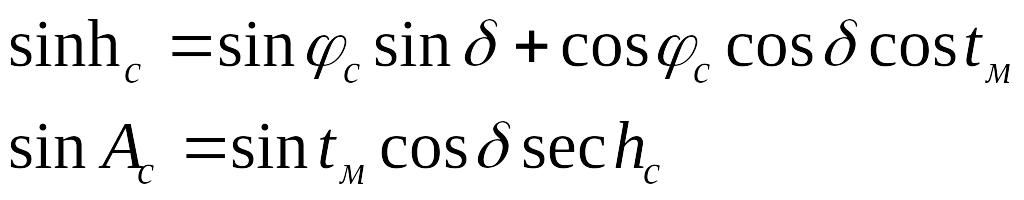
Э ту высоту наблюдатель измерил бы, если б находился в точке М_С. Через эту точку так же можно провести круг

равных высот с радиусом z_С = 90 - h_С. Разность n = h – h_C даст нам расстояние в милях между действительным и счислимым кругами равных высот. Проведя азимут А_С на светило и отложив на нём со своим знаком расстояние n, мы найдём определяющую точку К на действительном круге равных высот. Проведя через неё перпендикуляр, мы получим Высотную Линию Положения (ВЛП).

Измерив высоту другого светила и произведя аналогичные расчёты, мы получим вторую ВЛП. Пересечение обоих ВЛП даст нам обсервованное место судна М₀.

Учитывая то, что радиус круга равных высот, как правило, на несколько порядков больше расстояния между точками М_С и М, замена дуги на прямую линию практически не отразится на точности расчётов. То есть мы можем считать, что полученная нами точка М₀ практически совпадёт с действительной точкой М.

Переходя к обобщённому методу линий положения можно сказать, что навигационным параметром U, является истинная высота светила h, градиент g при этом равен единице, направление градиента совпадает с азимутом на светило.

Обобщённый порядок расчётов при графоаналитическом способе выглядит следующим образом:

1. Измеряются навигационные параметры U_о1 и U_о2;

2. рассчитываются счислимые параметры U_с1 и U_с2 (по формулам приведенным в таблице), на моменты измерений U_о1 и U_о2;

3. вычисляются разности

U₁= U_о1 - U_с1 ; U₂= U_о2 - U_с2;

4. рассчитываются модули g₁ и g₂ градиентов навигационных параметров и их направления ₁ и ₂;

5. по формулам

;

рассчитываются переносы;

6. на карте или планшете от счислимой точки по элементам₁, n₁ и ₂, n₂ строятся линии положения I–I и II–II, делается єто следующим образом:

1. Через счислимую точку при помощи транспортира проводится направление градиента ₁ первого навигационного параметра.

2. Вдоль направления градиента откладывается перенос n₁ по направлению, если перенос положителен, в противоположном – если отрицателен.

3. Через полученную точку жирным цветом проводится линия положения, обозначаемая с концов римской цифрой I.

4. Для построения второй линии положения производятся действия 1-3.

5. Пересечение высотных линий положения даёт нам обсервованную точку.

6. Снимаем координаты точки и невязку.

7. Производим оценку точности обсервованного места.

Следует учитывать, что производя построения на планшете, мы снимаем с него приращение координаты , и отшествие , далее при помощи углового масштаба, или формулы получаем приращение .

При аналитическом методе п.6, графических расчётов заменяется совместным решением системы уравнений:

( 0.4 )

, где

 отшествие.

Решив эту систему методом определителей и учитывая, что

cos(_c),

получим приращения координат:

( 4.0 )

,

где =₂-₁

далее определяем счислимые координаты:

₀=_с+ ₀=_с+

Как уже говорилось выше метод ЛП основывается на замене изолинии навигационного параметра, могущего иметь совершенно разные формы, на отрезок прямой, направленный по касательной к изолинии, естественно такая замена возможна лишь на небольших расстояниях, как правило, не превышающих 15-20 миль в приращениях координат. При получении приращений с большими значениями полученное место следует принять за первое приближение, а полученные координаты за счислимые и повторить рассчёты ещё раз.