3.4. Цилиндрическая равноугольная проекция

Наиболее важными требованиями к навигационной карте являются необходимость передачи углов без искажений и изображения локсодромии в виде прямой. Этим двум требованиям отвечает только равноугольная цилиндрическая проекция, названная по имени ее создателя проекцией Меркатора.

Найдем формулы для определения картографических координат х и y меркаторской проекции.

Н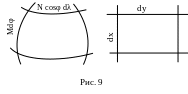 а рис. 9 показаны элементарный участок земного сфероида, ограниченный отрезкамимеридианов длиной Mdφ и отрезками параллелей длиной Ncosφdλ, и соответствующий участок карты со сторонами, равными dx и dy.

Расстояние между меридианами в цилиндрической проекции пропорциональны λ, поэтому dy = dλ.

Определим х = ƒ(φ) из условия равенства масштабов и по главным направлениям.

Масштабы вдоль меридиана и вдоль параллели, исходя из рис. 9 равны

;

Приравняв выражения для и , получаем

, откуда .

Такой интеграл был уже найден при выводе уравнения локсодромии (см.п.3.4). Воспользовавшись этим решением, можно записать

или

Величина х, выражающая расстояние на карте от экватора до параллели с широтой φ, называется меридиональной частью и обозначается D. Коэффициент пропорциональности зависит от масштаба изображения и от выбора единицы измерения. Если за единицу измерения принять 1 минуту дуги экватора (1 экв. милю), а частный масштаб изображения по экватору считать равным 1, то = 1 / arc1' = 3437,75 экв. мили. При таком значении величина D рассчитана с точностью до 0,1 по аргументу φ с шагом 1' и приведена в табл. 26 МТ-75.

На реальной карте, масштаб которой отличается от 1, расстояния от экватора до заданных параллелей определяются умножением величины на масштаб, отнесенный к экватору.

3.5 Построение промыслово-навигационного планшета в меркаторской проекции.

Все промыслово-навигационные планшеты строят в меркарторской проекции; за главную параллель принимают среднюю параллель изображаемого района.

При построении планшета может быть поставлена одна из двух задач:

• построить планшет в заданном масштабе данного района, границы которого определены приближенно;

• построить планшет определенного района, ограниченного заданными параллелями и меридианами, и вычислить масштаб данного планшета.

Для того, что бы получить единые меры длинны для горизонтальной и вертикальной рамок карты, нам необходимо вычислять меридиональные части, выраженные в экваториальных милях.

Длинна изображения одной экваториальной мили на меркарторской карте, выраженная в линейных мерах называется единицей карты.

Единица карты зависит от масштаба карты, который может быть отнесён к любой параллели, носящей название главной параллели.

Обозначив 1:Сэ главный масштаб по экватору, единицу карты можно рассчитать по следующей формуле:

e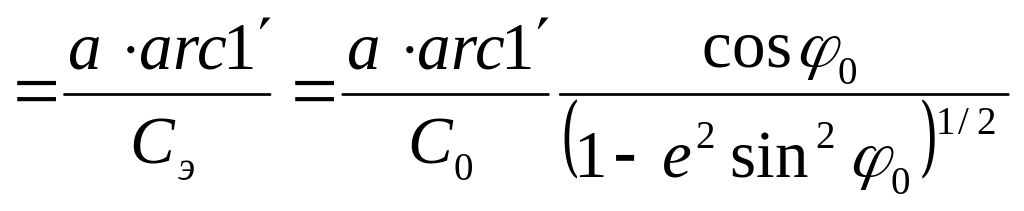 , где

1:С₀ – масштаб по главной параллели.

Иначе единицу карты можно найти из следующей формулы:

e , где

u – приведенная широта.

Впрочем, если имеются картографические таблицы, то единицу карты можно рассчитать значительно проще, воспользовавшись т.4 или т.2.

Если при построении планшета масштаб определяется тем условием, чтобы на него поместился заданный район, то единицу карты можно получить, разделив длину горизонтальной рамки карты на долготу, выраженную в минутах.

Порядок решения.

1. Вычисляют единицу карты е.

2. Рассчитывают размеры рамки планшета:

Горизонтальный размер

b = e (₂ - ₁)

Вертикальный размер

a = e D, где

D – разность меридиональных частей между крайними параллелями, выбирается из т.26 МТ-63.

3. Наносят рамку планшета на лист бумаги.

4. Рассчитывают расстояния в миллиметрах промежуточных параллелей:

y_i = e (D_i – D_S) или y_i = e (D_N – D_i).

Эти вычисления удобно свести в таблицу вида:

i

Di

Di

yi

5. Рассчитывают расстояния промежуточных меридианов от западной рамки планшета:

x_i = e (_W – _i) или x_i = e (_i – _E)

При условии, что расстояние между параллелями одинаково, достаточно его рассчитать один раз.

6. Наносят на планшет параллели и меридианы.

Пример. Рассчитать рамку и картографическую сетку промыслово-навигационного планшета в масштабе С=100000.

N=	70°	10' N		W=	29°	15'	E
S=	68°	40' N		E=	26°	30'	E
	10'				20'
0=	70°	00' N
1.Рассчитываем единицу карты:
e2=	0,0066934
a =	6378245000 мм
						6,4	мм
2.Рассчитываем длину горизонтальной рамки карты.
a = e(Ost -W)=			1050,8	мм
3.Рассчитываем расстояние между заданными меридианами
ai = e(i -W)
i = 28°55' E			=20;	ai = 127 мм
4.Рассчитываем длину b вертикальной рамки карты.
Меридиональные части
DN=	5973,6
DS=	5717,7
b = e(DN -DS)=			1629,5	мм
5.Рассчитываем расстояния от заданных параллелей до рамок карты
bi = e(Di -DS)
i			Di	D	bi мм
70	0	N	5944,3	29,3	187
69	50	N	5915,2	29,1	185
69	40	N	5886,3	28,9	184
69	30	N	5857,6	28,7	182
69	20	N	5829,2	28,4	181
69	10	N	5801,0	28,2	180
69	00	N	5773,0	28,0	178
68	50	N	5745,2	27,8	177
68	40	N	5717,6	27,6	176
7.Частный масштаб по параллели 1
		1,0
Ci=C/=		100000

Вопросы для самопроверки

1. Какие главные термины картографии должен знать судоводитель?

2. Что такое картографическая проекция и какие зависимости она определяет?

3. Что такое главные масштабы морской карты и как их применяют на практике?

4. Как разделяют картографические проекции по характеру искажений?

5. Какие виды картографических сеток используют в судовождении?

6. Какие бывают виды сеток стереографической проекции?

7. Как используется в судовождении меркаторская проекция?