4.2. Приклади характерних задач з розв’язанням

У задачах цього розділу пропонується самостійно зобразити цикли у відповідних координатах.

Задача 1. Визначити ККД циклу Отто, що складається з двох адіабат і двох ізохор. Відомий ступінь стиснення  газу, який можна вважати ідеальним.

Розв’язання. На ділянках кожної з адіабат тому розглянемо кількості теплоти і відповідно в процесі ізохорного охолодження від температури до і ізохорного нагрівання від до . З першого начала з урахуванням маємо

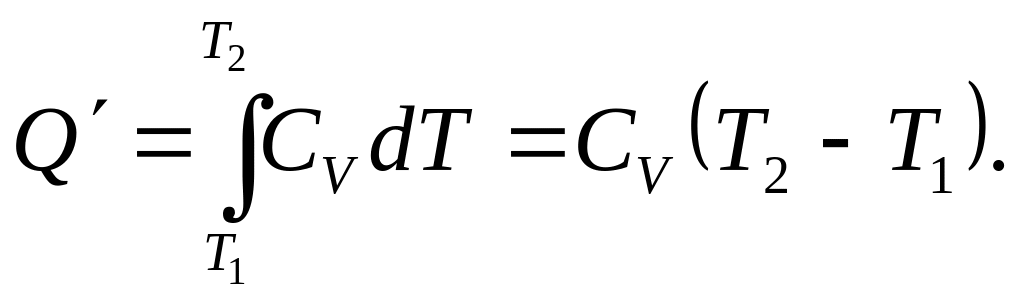(1)

Аналогічно

(2)

Оскільки і , визначаємо, що і

Отже, з (1) і (2) знаходимо

(3)

Використовуючи рівняння адіабати ідеального газу, пов’яжемо стани на адіабатичних ділянках і відповідно:

(4)

(5)

Перемноживши (4) і (5), отримаємо: або

(6)

Запишемо тепер результат (3) у вигляді

(7)

звідки, використовуючи (6), знайдемо

(8)

Оскільки за умовою  , рівність (5) можна записати як

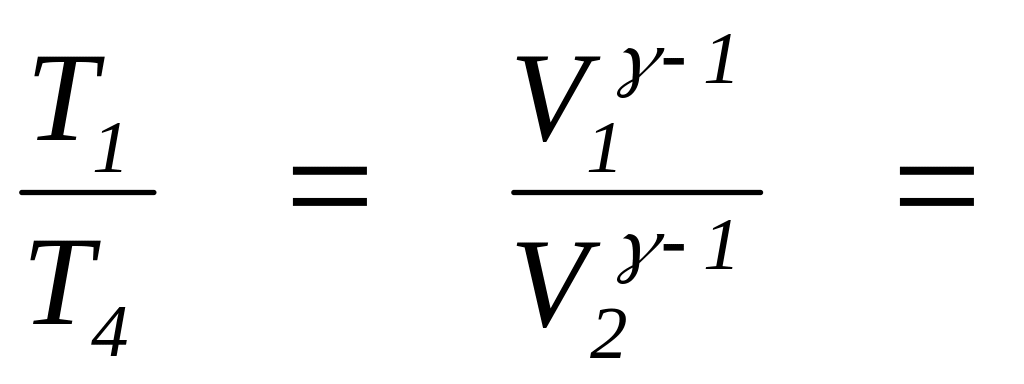 ^{1 } . (9)

Підставляючи (9) у (8), остаточно отримуємо:

 ^{1 } .

Задача 2. Визначити ККД циклу Ленуара, що складається з трьох процесів: ізобарного, ізохорного і процесу адіабатичного охолодження. Робочою речовиною є ідеальний газ. Відомою величиною вважати ступінь підвищення тиску.

Розв’язання. На ділянці адіабати маємо . Позначимо через кількість теплоти в процесі ізобарного стиснення при тиску від об’єму до . З першого начала запишемо:

(1)

де і – температури кінцевого і початкового станів відповідно. Для одного моля газу з термічного рівняння стану знаходимо:

(2)

звідки, підставляючи і в (1), з урахуванням отримуємо:

(3)

де

Нехай кількість теплоти на ділянці ізохори при збільшенні тиску від до . Оскільки , маємо

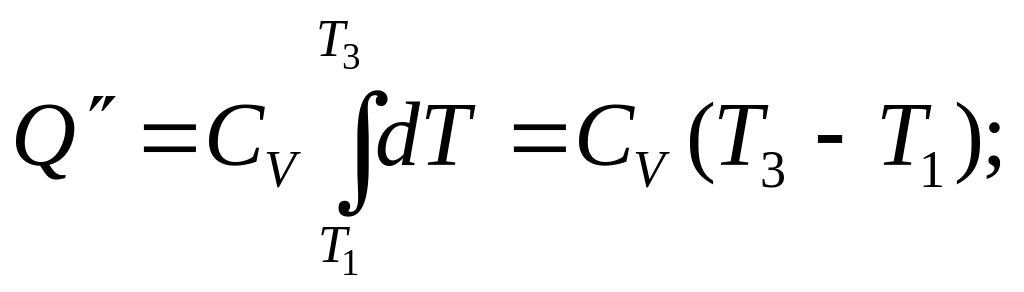(4)

тут аналогічно (2): і (4) набирає вигляду

(5)

Маючи на увазі, що за умовою і крім того для з (5) знаходимо

(6)

Оскільки і , маємо: Отже, використовуючи (3) і (6), отримуємо

(7)

На підставі рівняння адіабати для ідеального газу пов’яжемо стани і :

звідки

. (8)

Підставляючи (8) у (7), остаточно знаходимо

. (9)

Задача 3. Визначити ККД теплової машини з ідеальним газом, що працює за циклом Стірлінга, який складається з двох ізохор і двох ізотерм Відомими вважати ступінь стиснення і ступінь підвищення температури.

Розв’язання. Нехай T₂  T₁ і V₂  V₁; тоді за умовою

(1)

Для одного моля газу на ділянці ізотерми з урахуванням маємо

. (2)

На ділянці ізохори запишемо:

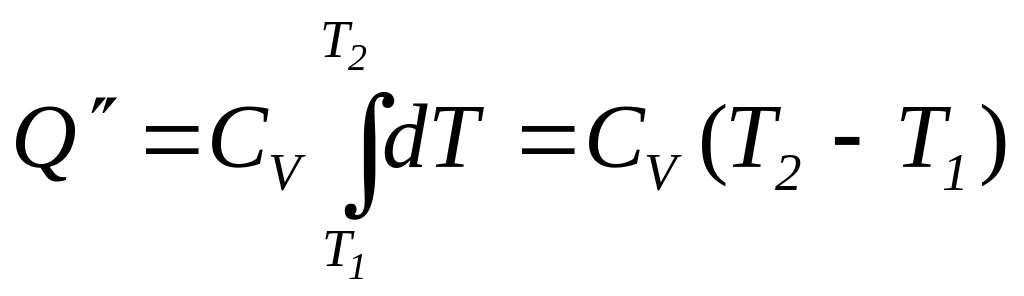. (3)

Аналогічно на ізотермі :

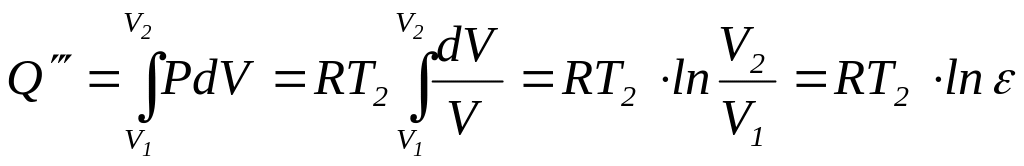, (4)

і на ізохорі :

(5)

Оскільки маємо і .

Отже, з (2)  (4) отримуємо:

(6)

З урахуванням і (1) остаточно знаходимо

Задача 4. Знайти ККД циклу чотирьохтактного двигуна Дизеля, що складається з таких процесів: 1) адіабатне стиснення від об’єму до , 2) ізобарне розширення від об’єму до , 3) адіабатне розширення від об’єму до , 4) ізохорне охолодження до початкового тиску. Вважати відомими ступінь стиску і ступінь попереднього розширення. Прийняти також, що робоча суміш є ідеальним газом.

Розв’язання. На обох ділянках адіабат маємо . Нехай кількість теплоти на ділянці ізобарного розширення із зміною температури від до , а на ділянці ізохорного охолодження зі стану в стан . Тоді в позначеннях умови задачі з першого начала запишемо:

(1)

З термічного рівняння стану для одного моля ідеального газу маємо:

(2)

Підставляючи (2) в (1), з урахуванням отримаємо:

(3)

де .

Для кількості теплоти (на цій ділянці ) знаходимо:

, (4)

і після використання рівняння Менделєєва-Клапейрона:

(5)

Через те, що і , маємо: і . Тоді з (3) і (5) отримуємо:

(6)

З урахуванням даних умови результат (6) можна переписати у вигляді

(7)

Пов’язуючи крайні точки адіабат циклу рівнянням , отримаємо:

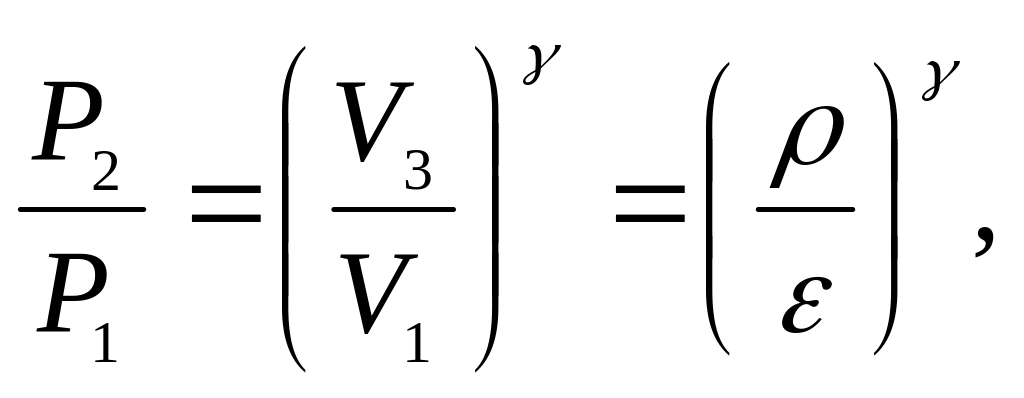
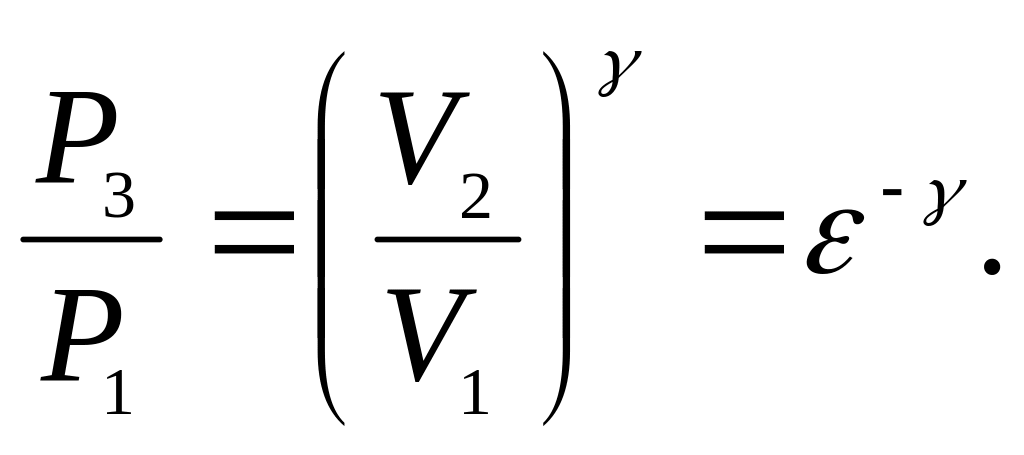(8)

Підставляючи (8) в (7), остаточно знайдемо

Задача 5. Знайти ККД циклу, що складається з двох адіабатичних і двох ізобаричних процесів, якщо відомий ступінь підвищення тиску при адіабатичному стисненні. Робочою речовиною є ідеальний газ.

Розв’язання. Аналіз даного кругового процесу дозволяє зробити висновок, що система отримує тепло на ділянці ізобаричного (при ) розширення від об’єму, скажімо, до . Отже, відповідну кількість теплоти можна записати у вигляді

, (1)

де і – температури в станах відповідно і .

Кількість теплоти , відданої системою на ділянці ізобаричного (при ) стиснення від об’єму до , знайдемо аналогічно:

, (2)

де і – температури в станах відповідно і .

Використовуючи (1), (2), і з урахуванням термічного рівняння стану для шуканого ККД запишемо

(3)

Параметри у вершинах циклу можна пов’язати рівняннями адіабат:

(4)

де . Перемножуючи рівності (4), знайдемо:

. (5)

Оскільки за умовою , за допомогою співвідношення (5) для виразу (3) отримаємо:

(6)

Використовуючи першу з рівностей (4), запишемо

(7)

звідки остаточно знайдемо

Задача 6. Визначити ККД “усіченого” циклу Карно, який складається з ізотерми, адіабати і процесу, в якому абсолютна температура лінійно зменшується в разів із зростанням ентропії.

Розв’язання. Знайдемо кількості теплоти і відповідно на ізотермічній ділянці циклу і на ділянці, де абсолютна температура лінійно зменшується від до із зростанням ентропії. Позначимо граничні значення ентропії через і . Тоді на підставі (3.4) запишемо

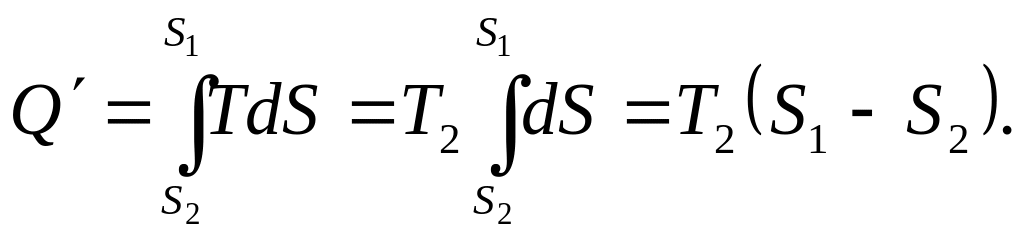(1)

Оскільки на цій ділянці циклу маємо тобто на ізотермі робоче тіло віддає тепло.

Для вирахування запишемо рівняння для лінії, що проходить через точки і :

(2)

Тоді

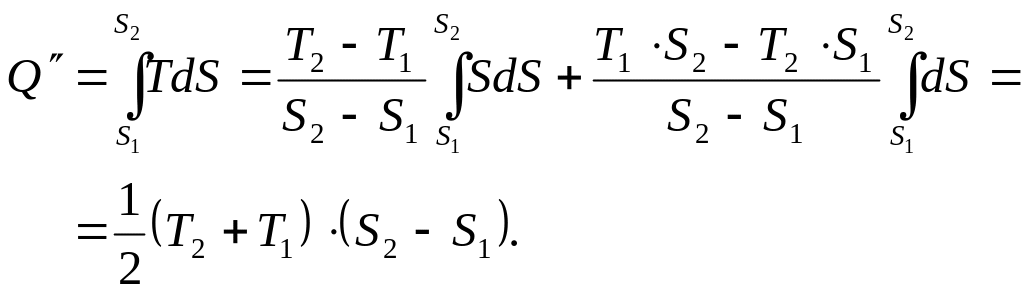(3)

Оскільки , то на цій ділянці циклу робоче тіло поглинає тепло. Звідси маємо: і

Отже, для шуканого значення ККД запишемо:

Підставляючи сюди (1) і (3), з урахуванням остаточно знайдемо

Задача 7. Визначити ККД циклу з ідеальним газом, який складається з ізохори, ізобари і процесу, в якому тиск змінюється за законом , а температура зменшується у разів.

Розв’язання. Позначимо максимальну температуру в циклі через Т₁, а відповідні значення тиску і об’єму через Р₂ і V₂. Позначимо також через Р₁ і V₁ тиск і об’єм в стані з мінімальною температурою Т₂ циклу, а через Т₃  температуру в стані з тиском Р₂ і об’ємом V₁.

Кількість теплоти Q₁₂ в процесі стиску газу за законом P = aV від об’єму V₂ до V₁ запишемо з першого начала:

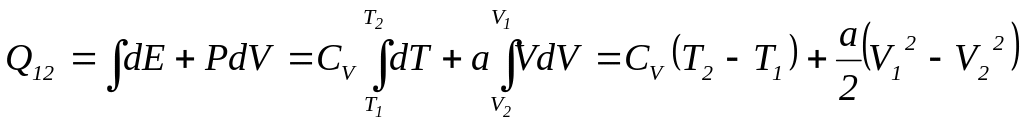. (1)

Для одного моля з термічного рівняння стану знайдемо V= = , звідки

. (2)

З урахуванням (2) перепишемо (1) у вигляді

. (3)

На ділянці ізохори (dV= 0) аналогічно маємо

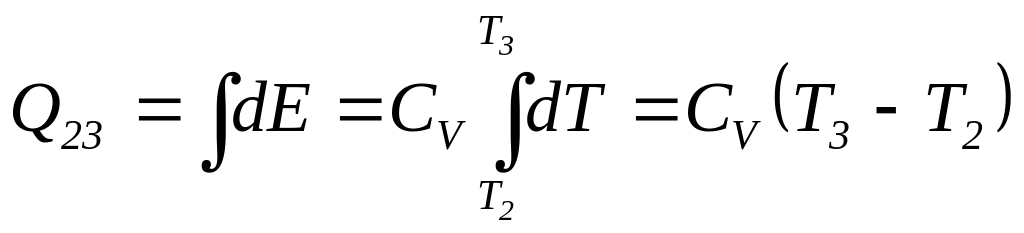. (4)

Для ізобаричного процесу знаходимо:

. (5)

Відзначимо, що Q₁₂  0, Q₂₃  0, Q₃₁  0. Отже, Q₂ = , Q₁ = Q₂₃ + Q₃₁. Додаючи (4) і (5), запишемо

. (6)

З рівняння Менделєєва-Клапейрона з урахуванням зв’язку P = aV і співвідношення (2) знайдемо проміжну температуру Т₃:

. (7)

Підставляючи (7) у (6), для ККД даного циклу з (3) і (6) отримуємо:

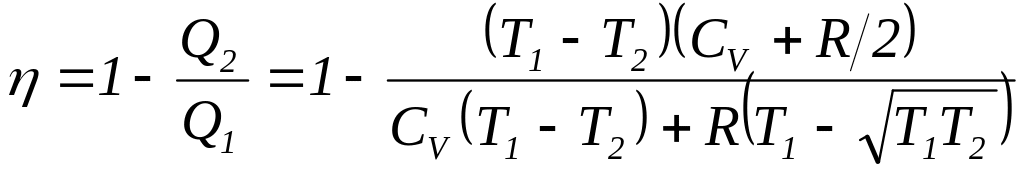
або після алгебраїчних перетворень (беручи до уваги, що R = C_P  C_V, ):

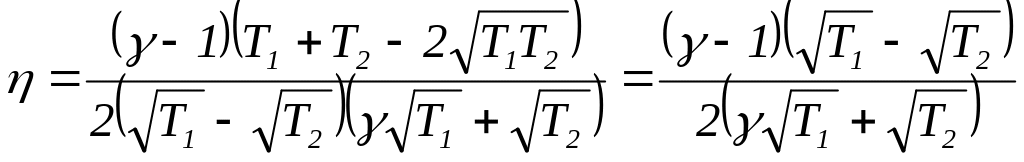. (8)

Оскільки за умовою , шуканий ККД остаточно набирає вигляду:

.

Задача 8. Визначити ККД циклу з ідеальним газом, який складається з двох ізобар і двох ізохор. Відоме відношення  максимальної до мінімальної температури в циклі, і що дві вершини циклу належать одній ізотермі.

Розв’язання. Робота W, яку виконує система за цикл, може бути записана у вигляді

. (1)

Оскільки в координатах P,V даний цикл має форму прямокутника, а геометричний зміст інтегралу в (1) є площа циклу в цих координатах, знайдемо:

, (2)

де P₂, P₁ і V₂, V₁  граничні значення координат, які обмежують ділянки ізохор та ізобар циклу.

На двох з чотирьох ділянок циклу кількість теплоти буде додатним. Це відрізки ізохорного (при V = V₁) збільшення тиску від Р₁ до Р₂ та ізобарного (при Р = Р₂) розширення від V₁ до V₂. Отже, кількість теплоти Q₁, яку отримала система за цикл, після інтегрування Q за цими ділянками дорівнюватиме

, (3)

де Т₂  температура в стані (P₂, V₁), Т₃  в стані (P₂ , V₂), Т₁  в стані (P₁, V₁).

З (3) і (2) запишемо ККД циклу:

. (4)

Позначивши температуру стану (P₁, V₂) через Т₄, пов’яжемо рівнянням Менделєєва-Клапейрона (для 1 моля) “вершинні” стани циклу:

P₂V₁ = RT₂, P₁V₂ = RT₄, P₂V₂ = RT₃, P₁V₁ = RT₁ . (5)

Перемноживши перше і друге, а потім третє й четверте з рівностей (5), і порівнюючи результати, одержимо

Т₁Т₃ = Т₂Т₄ . (6)

З умови задачі видно, що Т₁  мінімальна температура циклу, Т₃  максимальна, а Т₂ = Т₄. Отже, з (6) маємо:

. (7)

Розкриваючи дужки в чисельнику формули (4) та використовуючи рівності (5) і (7), знайдемо

. (8)

Маючи на увазі, що для одного моля R = C_P  C_V, а за умовою , після простих алгебраїчних перетворень приводимо результат (8) до кінцевого вигляду

.

Задача 9. Цикл складається з ізобари, ізохори і процесу, в якому тиск лінійно зменшується з підвищенням у  разів об’єму ідеального газу. Знайти умову, за якою система на останній ділянці циклу тільки віддає тепло, та визначити для цього випадку ККД циклу.

Розв’язання. Віддача системою теплоти (Q  0) на діагональній ділянці циклу відповідає зменшенню ентропії (S  0) на всій цій ділянці. Отже, адіабати з сім’ї адіабат ідеального газу можуть перетинати цю ділянку лише в одній точці кожна, а їхній нахил в точках перетину повинен бути менший за нахил самої діагональної ділянки. Саме ця умова забезпечує зменшення ентропії, а тому й віддачу теплоти на даному відрізку циклу. Математично її можна записати у вигляді

, (1)

де P₁, V₁  мінімальні тиск і об’єм у циклі, P₂, V₂  максимальні,  коефіцієнт нахилу діагональної ділянки циклу. Ліва частина нерівності (1) виражає похідну в точці (V₁, P₂) від тієї адіабати, яка проходить через цю вершину циклу. Оскільки для адіабати , з (1) знаходимо:

або

. (2)

Далі позначимо . Оскільки за умовою , нерівність (2) можна переписати як

або

; . (3)

Нерівності (3) виражають для параметрів циклу , ,  умови, за яких на всій діагональній ділянці циклу система тільки віддає тепло.

Відзначимо, що лише на ізохорному відрізку (при збільшенні тиску від Р₁ до Р₂) система поглинає тепло. Отже,

, (4)

де Т₂  температура в стані (P₂, V₁), Т₁  в стані (P₁, V₁). За допомогою рівняння Менделєєва-Клапейрона вираз (4) запишемо у вигляді

. (5)

Роботу W, яку газ виконав за цикл, знайдемо як площу циклу:

. (6)

Отже, для ККД  циклу за умов (3) маємо:

. (7)

Враховуючи, що R = C_P  C_V і , остаточно одержимо:

.
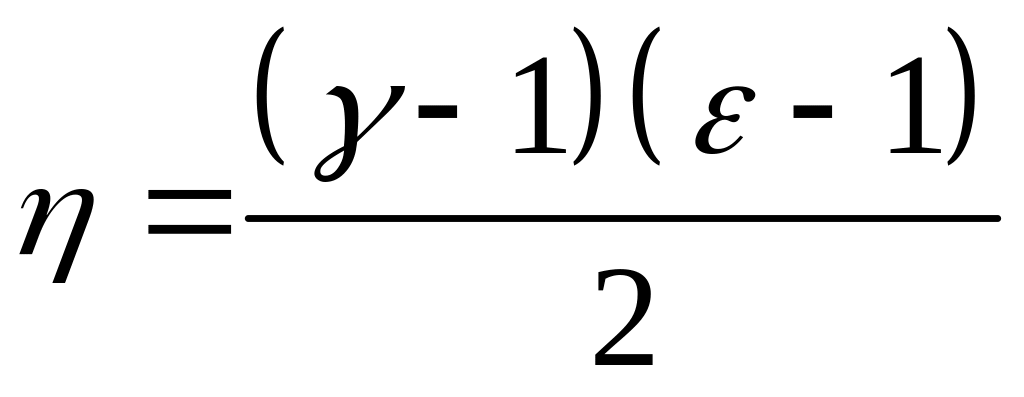