– Congruência de triângulos
3.1 – Definição
Um
triângulo é congruente (símbolo
)
a outro se, e somente se, é possível estabelecer uma
correspondência entre seus vértices de modo que:
Seus lados são ordenadamente congruentes aos lados do outro e
Seus ângulos são ordenadamente congruentes aos ângulos do outro.
A congruência entre triângulos é reflexiva, simétrica e transitiva.
3.2– Casos de congruência
A definição de congruência de triângulos dá todas as condições que devem ser satisfeitas para que dois triângulos sejam congruentes. Essas condições (seis congruências: três entre lados e três entre ângulos) são totais. Existem condições mínimas para que dois triângulos sejam congruentes. São os chamados casos ou critérios de congruência.
1º Caso – LAL – postulado
2º
Caso – ALA
3º
Caso – LLL
4º Caso – LAAO
Se dois triângulos têm ordenadamente congruentes um lado, um ângulo adjacente e o ângulo oposto a esse lado,então esses triângulos são congruentes.
Caso especial:
Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa,então esses triângulos são congruentes.
37) Considere os triângulos T1, T2, ..., etc, abaixo. Assinale os pares de triângulos congruentes e indique o caso de congruência:
70°
T1
3
4
60°
1
2
T2
8
35°
3
T3
35°
25°
10
T4
35°
T5
3
8
T6
3
4
6
60°
T7
1
2
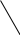
T8
4
3
70°
80°
5
20º
T9
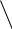
6
T10
4
3
T11
25º
35º
10
80º
T12
5
20º
38) Nos casos a), b) e c) abaixo, selecione os triângulos congruentes e indique o caso de congruência:
4
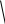
4
I
II
III
6
60º
60º
60º
6
6
4
80º
I
45º
80º
II
45º
III
80º
45º
5
5
5
5
13
I
5
13
.
II
13
.
III
5
.
39) Determine o valor da incógnita (segmentos com “marcas iguais” são congruentes).
b) c)
x
x
100º
25º
x
A
A
65º
B = AC e) f)
x
B
C
x
x
4 – Polígonos
4.1 – Definição
Seja
(P1,
P2,
..., Pn)
um conjunto ordenado de n
pontos de um plano,
,
de modo que três pontos consecutivos quaisquer, P1P2P3,
P2P3P4,
..., Pn-1PnP1
e PnP1P2
sejam não-colineares, e considere os segmentos
,
,
...
e
.
Chama-se polígono P1P2...Pn à união dos segmentos e , , ... e os quais são chamados de lados do polígono, enquanto os pontos são os vértices do polígono.
Assim, cada figura abaixo representa um polígono, e cada um deles corresponde a um conjunto ordenado de cinco pontos (P1, P2, P3, P4, P5).
Um polígono é também chamado de contorno poligonal fechado.
Dois lados de um polígono são consecutivos quando têm uma extremidade comum. Por exemplo: P1 P2 e P2P3, ou P1P2 e PnP1.
Um polígono é simples, se quaisquer dos lados não-consecutivos não se interceptam.
Assim, as figuras 1 e 2 representam polígonos simples.
A figura 3 não representa um polígono simples. Esse tipo de polígono é chamado de polígono estrelado ou polígono entrelaçado.
O nosso estudo limita-se apenas aos polígonos simples, que serão daqui por diante chamados simplismente de polígonos.
Num polígono, o número de vértices é igual ao número de lados.
Perímetro é a soma das medidas dos lados do polígono.
4.2 – Nomenclatura
De acordo com o número de lados, alguns polígonos recebem nomes especiais.
3 |
Triângulo |
4 |
Quadrilátero |
5 |
Pentágono |
6 |
Hexágono |
7 |
Heptágono |
8 |
Octógono |
9 |
Eneágono |
10 |
Decágono |
11 |
Undecágono |
12 |
Dodecágono |
13 |
Tridecágono |
20 |
Icoságono |
4.3 – Polígono Convexo
Um polígono é convexo se sua região poligonal é um conjunto convexo de pontos, ou seja, o segmento que liga dois pontos quaisquer desse conjunto está contido nele.
Assim o polígono ABCDE da figura é um polígono convexo.
Caso contrário, é chamado de não-convexo. Assim, o polígono FGHLM é um polígono não-convexo.
4.4 – Ângulos de um polígono convexo
Ângulo interno de um polígono é convexo é um ângulo formado por dois lados consecutivos do polígono.
Â
ngulo
externo de um
polígono convexo é um ângulo adjacente a um ângulo interno desse
polígono.
Na figura, o ângulo ADC é um ângulo interno, e o ângulo CDE é um ângulo externo do quadrilátero ABCD.
Decorre
dessas definições que
.
4.5 – Ângulos internos
A
soma das medidas dos ângulos internos de um polígono convexo de n
lados é
.
Unindo um dos vértices aos outros n – 3, convenientemente escolhidos, obteremos n – 2 triângulos. A soma das medidas dos ângulos internos do polígono é igual a soma das medidas dso ângulos internos dos n – 2 triângulos.
Si = (n – 2) . 180º
Portanto:
Assim,
um quadrilátero é decomposto em 2 triângulos, um pentágono, em
três triângulos, e assim por diante.
4.6 – Ângulos externos
Em todo polígono convexo, tomando-se um ângulo externo para cada vértice, a soma de suas medidas é 360º.
Como cada ângulo externo é suplementar do ângulo interno adjacente, a soma dos ângulos internos com os ângulos externos dá 180º. n . Subtraindo a soma dos ângulos internos, que é (n – 2) . 180º , resulta que a soma dos ângulos externos é 2 . 180º, ou seja, 360º.
Se = 360º
Conclusão:
4.7 – Polígono regular
Um polígono é equilátero se possui os lados congruentes entre si, e equiângulo, se possui os ângulos congruentes entre si.
B
Assim, o quadrilátero da figura 1 é equilátero e o da figura 2 é equiângulo.
figura 2
figura 1
C
Um polígono convexo é regular se ele é equilátero e equiângulo.
Observação:
Num polígono regular existe um ponto que dista igualmente dos vértices; ele é chamado centro do polígono.