3. Термодинамічні основи холодильних машин

3.1. Ідеальний газ та його властивості

Ідеальним називається газ у якому молекули не пов’язані силами взаємного тяжіння та розмірами яких ми нехтуємо. Ідеальний газ є газом досконалим, він повністю підпорядковується газовим законам Бойля-Маріата та Гей-Люссака. Реальні гази відступають від вказаних законів, і якщо до них і застосовують ці закони, то при цьому допускають деяке наближення. Теплоємність реальних газів, на відміну від ідеального, є величина перемінна.

Для ідеальних газів справедливими є закони:

1. Закон Бойля-Маріотта:

В процесах, які протікають за постійної температури, тиск газу змінюється обернено пропорційно його об’єму (В процесах, які протікають за постійної температури, добуток тиску на питомий об’єм є величина постійна)

або ; (3.1)

2. Закон Гей-Люссака

В процесах, які протікають за постійного тиску, збільшення об’єму газу пропорційно підвищенню його температури (Відношення об’ємів газів в процесах, що протікають за постійного тиску, буде прямо пропорційно відношенню абсолютних температур)

(3.2)

3. Закон Шарля

В процесах, які протікають за постійного об’єму, збільшення тиску газу пропорційно підвищенню його температури (Відношення тисків газу в процесах, що протікають за постійного об’єму, буде прямо пропорційно відношенню абсолютних температур)

(3.3)

4. Об’єднаний закон Бойля-Маріотта та Гей-Люссака

Для процесів які протікають при зміні всіх параметрів справедливе твердження:

добуток тиску на об’єм поділені на абсолютну температуру, для будь-якого моменту процесу є величина постійна

(3.4)

Наслідком законів Бойля-Маріотта і Гей-Люссака є характеристичне рівняння стану ідеального газу, виведене Клапейроном, що для 1кг газу має вигляд

, (3.5)

де р – абсолютний тиск газу, Па;  –питомий об’єм газу, м³/кг; R – газова стала, для будь-якого газу R=8314/, Дж/(кг·К); µ – молекулярна маса газу, кг/кмоль; Т – абсолютна температура, К.

3.2.Основні термодинамічні процеси

Зміна стану 1кг газу, який визначається параметрами р, , Т, може відбуватися:

а) під впливом надання чи відведення теплоти;

б) від зовнішньої механічної дії.

Рівняння, що враховує всі зміни, які відбуваються в процесі зміни стану, має вигляд

. (3.6)

В рівнянні фігурує три фактори: теплота, внутрішня енергія та зовнішня механічна робота. В залежності від характеру та ступеня зміни вказаних факторів будемо мати різні умови протікання процесу. Розглянемо основні процеси.

Процес за постійного об’єму: =сonst. Для такого процесу справедливим є рівняння Шарля (3.3). Тиск в процесі з постійним об’ємом змінюється прямо пропорційно температурі. Зовнішня робота в таких процесах , оскільки об’єм не змінюється, а все підведене тепло Q витрачається на зміну внутрішньої енергії U. При відведенні теплоти, відбувається зменшення внутрішньої енергії. Наглядно ці процеси можна відобразити рисунком:

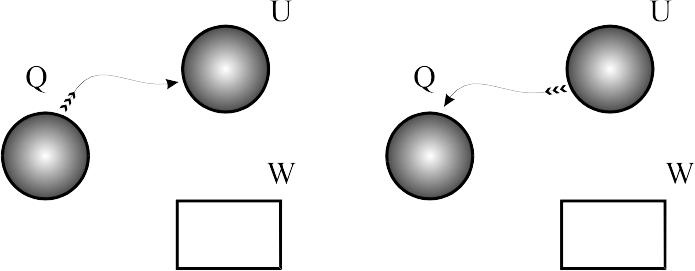
Процес за постійного тиску: р=сonst. Для такого процесу справедливим є рівняння Гей-Люсака (3.2). Об’єм в процесі з постійним тиском змінюється прямо пропорційно зміні абсолютних температур. Зовнішня робота в таких процесах . Так як температура газу при розширенні збільшується, то збільшується і внутрішня енергія. Отже теплота підведена в ізобарних процесах витрачається на виконання зовнішньої роботи і збільшення внутрішньої енергії. При відведенні теплоти відбуваються зворотні зміни.

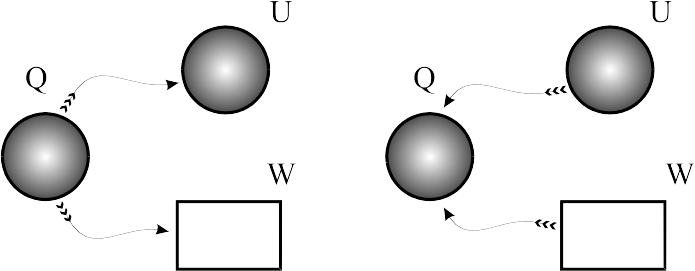
Процес за постійної температури: Т=сonst. Умови протікання ізотермічного процесу дозволяють скористатися рівнянням Бойля-Маріотта (3.1). Оскільки в таких процесах внутрішня енергія не змінюється, то вся підведена до газу теплота витрачається на виконання зовнішньої роботи. При відведенні теплоти буде виконуватися робота проти внутрішніх сил.

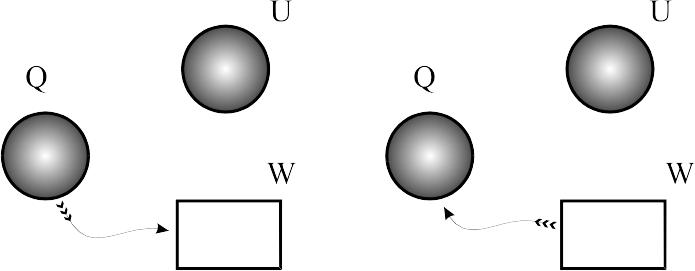
Адіабатний процес. Адіабатним називається процес, в якому не бере участь зовнішня теплота. Рівняння адіабатного процесу: р^k=сonst. Тоді

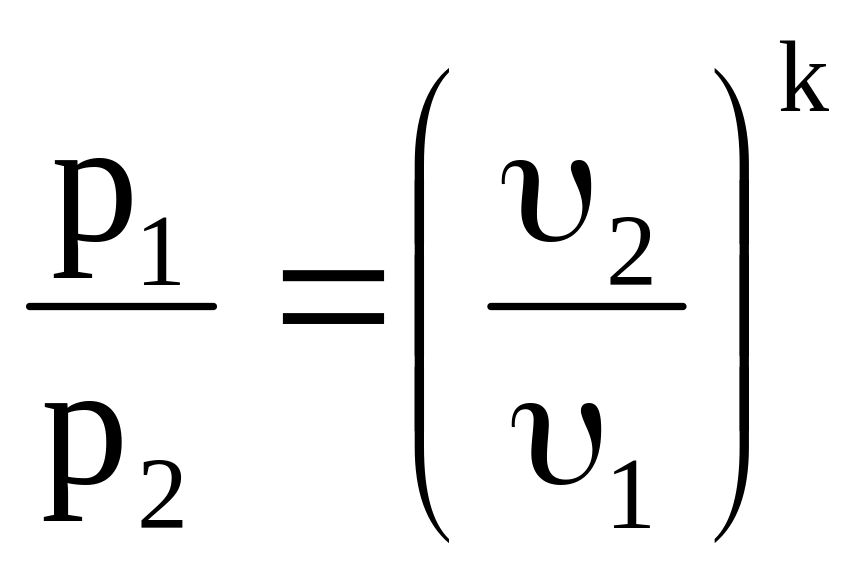, та . (3.7)

В процесі адіабатного розширення зовнішня робота виконується завдяки зменшенню внутрішньої енергії, температура при цьому знижується. В процесі адіабатного стискання теплота, еквівалентна зовнішній роботі, витрачається на збільшення внутрішньої енергії, температура при цьому зроста.

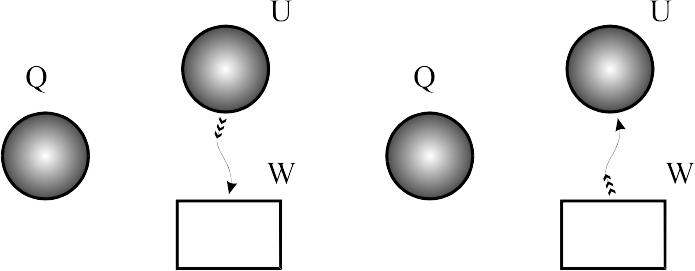
Поряд з розглянутими процесами, можливі процеси, в яких не має таких наочно виражених ознак. Ми говорили, що підведена теплота витрачається на зміну внутрішньої енергії або на виконання зовнішньої роботи. Для різних процесів частка теплоти, що витрачається на зміну внутрішньої енергії, набуває свого особливого числового значення. Процеси, що протікають таким чином називаються політропними. Розглянемо ізотермічний та адіабатний процеси. Вони різняться корінним чином. У першому випадку вся підведена теплота витрачається на виконання зовнішньої роботи, а внутрішня енергія не змінюється, в другому ­- вся робота виконується за рахунок внутрішньої енергії, а надходження теплоти відсутнє. Між цими процесами легко уявити цілий ряд політропних процесів які будуть носити деякий проміжний характер. Оскільки крайні випадки процесів описуються схожими рівняннями: р=сonst та р^k=сonst то логічно зробити висновок, що всі проміжні процеси можуть бути описані схожим рівнянням рⁿ=сonst, при цьому для кожного з них, частка теплоти, що витрачається на зміну внутрішньої енергії, буде своя, і, отже, кожний процес буде мати свій відповідний показник степені n.

А оскільки n може змінюватися від 0 до , то всі процеси можуть розглядатися як політропні, з певним показником степені. Так при n=0 p=const – процес ізобарний; при n=1 р=сonst – ізотермічний; при n= – ізохорний; при n=k – адіабатний. В залежності від величини n процеси можуть протікати при збільшенні, зменшенні чи незмінній внутрішній енергії. Якщо n<1, то в процесі розширення з припливом теплоти виконується робота та збільшується внутрішня енергія, при стисканні – відводиться теплота і зменшується внутрішня енергія.

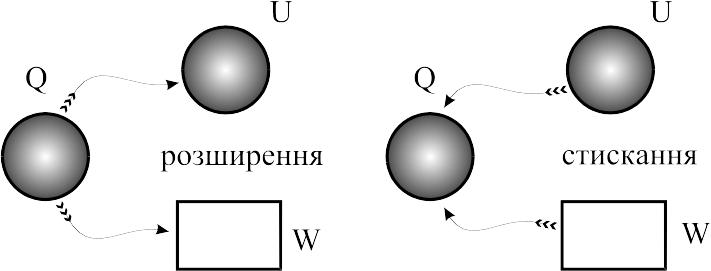
Якщо 1<n<k (k=1,4 для двоатомних газів), то при розширенні з припливом теплоти виконується робота та зменшується внутрішня енергія, при стисканні – відводиться теплота і збільшується внутрішня енергія.

Якщо n>k, то за рахунок внутрішньої енергії виконується робота та теплота віддається зовнішньому джерелу; за рахунок виконання роботи та підведення теплоти зростає внутрішня енергія.