9. Термоелектричні холодильні машини

Термоелектричні холодильні машини, в яких використовуються нові напівпровідникові матеріали, широко використовуються в різних охолодних пристроях.

В сучасних термоелементах в області температур навколишнього середовища максимальна різниця температур на спаях досягає 70-90ºС. В багатокаскадних пристроях ця різниця температур може досягати більше 100ºС.

Таким чином, різниця температур, яку можна отримати в термоелектричних холодильних машинах, достатня для використання цього способу охолодження в різних галузях науки та техніки. Ряд особливостей термоелектричних охолодних пристроїв, зокрема відсутність механічних рухомих елементів, сприяє їхньому поширенню.

9.1.Схема та цикл короткозамкненого термоелектричного ланцюга

При замкненні електричного ланцюга термопари, в яких створена та підтримується постійна різниця температур, одночасно виникають три термоелектричних ефекти: Зеєбека, Пельтьє та Томсона (див.1.5). Крім того, в термопарі, якщо існує різниця температур, теплота передається від гарячого спаю до холодного за рахунок теплопровідності, а електричний струм викликає виділення теплоти Джоуля.

Для визначення взаємозв’язку між цими ефектами уявимо термопару у вигляді замкненого ланцюга і розглянемо її як теплову машину, робочою речовиною в якій є електронний газ. Схема та цикл в Т-s діаграмі такої машини наведено на рис.9.1. Будемо рахувати, що незворотні процеси теплопровідності та виділення теплоти Джоуля відсутні. Ділянки 1-4 та 2-3 в циклі 1-2-3-4 відповідають протіканню деякої кількості електрики через контакти між елементами термопари. Ділянки 1-2 та 3-4 характеризують зміну кількості електрики, яка відбувається внаслідок руху струму через напівпровідникові елементи термопари І та ІІ. Теплота Пельтьє на ділянці 2-3 виділяється, на ділянці 1-4 поглинається. Теплота Томсона на ділянці 3-4 виділяється і поглинається на ділянці 1-2. Робота циклу 1-2-3-4, яку здійснює термо-е.р.с. під час протікання визначеної кількості електрики q_t у відповідності до першого закону термодинаміки, дорівнює різниці підведеної та відведеної теплоти, а саме w_ц ~ пл.1-2-3-4 = (пл.2-3-k-n + пл.1-2-n-m) – (пл.1-4-с-m + пл.4-3-k-c) або

. (9.1)

Згідно другому закону термодинаміки можна визначити зміну ентропії на будь-якій ділянці циклу. В замкненому циклі приріст ентропії дорівнює нулю, тоді

. (9.2)

Рівняння (9.1) та (9.2) тим точніше описують реальний процес, чим менша різниця температур (T_г–Т_х). Для граничного випадку (T_г–Т_х)=dT можна записати:

; (9.3)

. (9.4)

Термо-е.р.с. на кінцях розімкненого ланцюга

. (9.5)

Скориставшись рівняннями (9.3) та (9.5) отримаємо перше термоелектричне співвідношення

. (9.6)

Підставляючи (9.6) в (9.4) отримуємо друге співвідношення

. (9.7)

Із (9.6) та (9.7) отримуємо ще одне важливе співвідношення

. (9.8)

Кількість теплоти Q, яку виділяє гарячий спай, буде більшою, ніж кількість теплоти Q₀, яку поглинає холодний спай, на величину затрат електроенергії від зовнішнього джерела. Ця енергія витрачається на здійснення роботи W переміщення струму проти різниці електричних потенціалів, що виникають у ланцюгу при T_х≠Т_г у відповідності до закону Зеєбека.

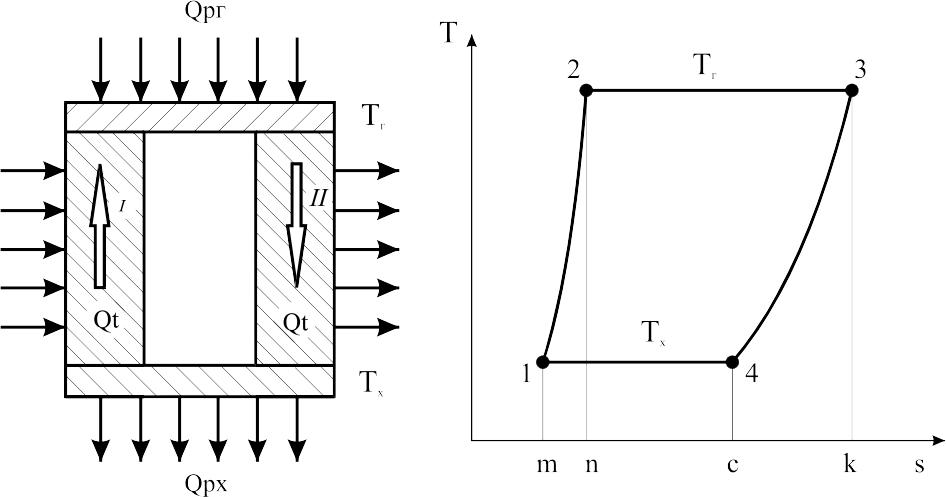
Рис.9.1. Схема короткозамкненого термоелемента та цикл електронного газу в Т-s діаграмі

Скориставшись (1.44) та (1.45) знаходимо холодильний коефіцієнт зворотного циклу термоелемента, в якому роль робочої речовини виконує електронний газ та відсутні необоротні втрати

. (9.10)

Величина ε співпадає з холодильним коефіцієнтом циклу Карно, оскільки теплота в циклі підводиться та відводиться при постійних температурах, а необоротні втрати відсутні.

В дійсності робота термоелектричної холодильної машини супроводжується незворотними втратами двох типів: по-перше, розповсюдження струму супроводжується джоульовими втратами і, по-друге, по провідниках, з яких складається ланцюг, неперервно йде теплота від гарячого спаю до холодного за рахунок теплопровідності. Скориставшись формулами (1.46) та (1.47), які враховують ці втрати, холодильний коефіцієнт дійсного циклу термоелектричної холодильної машини може бути визначений за формулою

. (9.11)

Порівняння (9.2) та (9.1) показує, що незворотні втрати знижують значення холодильного коефіцієнта. При цьому очевидно, що чим меншим буде опір провідників, з яких складається ланцюг, чим менші коефіцієнти теплопровідності цих провідників і чим вище значення коефіцієнта термо-е.р.с., тим більше значення холодильного коефіцієнта.