3.6. Оборотні зворотні цикли в умовах різноманітних зовнішніх джерела

Розглянемо, як впливає величина температури джерел та її сталість на ефективність холодильних циклів.

Якщо температури джерел не змінюється в процесі теплообміну, то єдино можливими циклами, для яких будуть дотримуватися умови оборотності, будуть цикли Карно 1-2-3-4 та узагальнений цикл Карно (регенеративний) 5-2-3-6 (рис.3.8), у якому s₂-s₅=s₃-s₆. У цих циклах ізотермічні процеси теплообміну між робочою речовиною та джерелами проходять при постійних температурах, а різниця температур є нескінченно малою. Процеси стискання і розширення робочої речовини в циклі Карно проходять ізоентропно, тобто оборотні. У регенеративному циклі збільшення ентропії робочої речовини під час стискання дорівнює зменшенню ентропії під час розширення, відповідно сумарна зміна ентропії в цих двох процесах дорівнює нулю. Використання такого роду циклів-зразків можливо тільки в тому випадку постійності температури джерел.

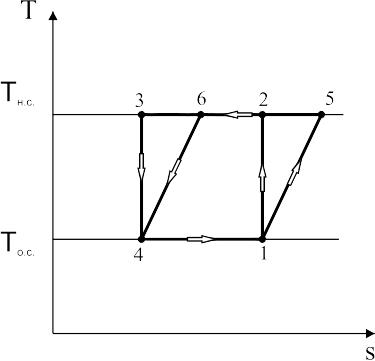
Рис.3.8. Цикл Карно та “узагальнений” цикл Карно в Т-s діаграмі

Температури джерел по різному впливають на ефективність циклів. Цей вплив можна побачити знайшовши диференціали рівняння (3.12) за температурами джерел:

; , звідки . (3.25)

З останньої нерівності робимо висновок, що зміна температури навколишнього середовища менше впливає на холодильний коефіцієнт, ніж зміна температури джерел низької температури. При цьому необхідно пам’ятати, що мають на увазі зміну зовнішніх умов проведення циклу, після якої процеси теплообміну проходитимуть за сталих температур.

Однак на практиці зовнішні джерела часто змінюють свою температуру в процесі теплообміну (нагріваються чи охолоджуються), тому для виконання умов зовнішньої оборотності температура робочої речовини повинна змінюватися так само, як змінюється температура зовнішніх джерел. При цьому у кожній точці процесу повинна дотримуватися термічна рівновага між робочою речовиною і зовнішніми джерелами. Для такого випадку цикл Карно вже не можна розглядати як цикл-зразок, тому що це призведе до виникнення зовнішньої необоротності.

Ізотермічні ділянки, характерні для циклу Карно, повинні бути замінені зовнішньо оборотними процесами, при яких температура робочої речовини в точності відповідає змінам температури зовнішніх джерел. Цілком оборотний зворотний цикл із перемінними температурами в процесах підведення і відведення теплоти зображено на рис.3.9. – цикл 1-2-3-4. Його можна уявити як сукупність елементарних циклів Карно (а-b-c-d). Холодильний коефіцієнт такого елементарного циклу:

. (3.26)

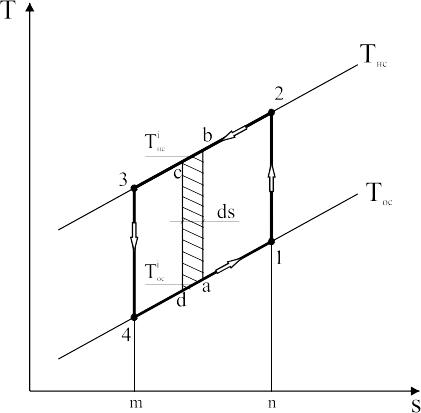
Рис.3.9. Цикл Лоренца у Т-s діаграмі

Холодильний коефіцієнт циклу 1-2-3-4:

(3.27)

Величини q_o і q можна виразити через середні еквівалентні температури T_осm і Т_нсm:

; . (3.28)

Кількість підведеної q_o і відведеної теплоти q еквівалентно площам т-4-1-n та m-3-2-n відповідно. Отже, середні еквівалентні температури можна розглядати як висоти прямокутників, рівновеликих відповідно площам т-4-1-n та m-3-2-n із основою, рівною

s₁-s₄=s₂-s₃.

На підставі виразів (3.28) отримаємо

. (3.29)

Цикл 1-2-3-4 називається циклом Лоренца. Будь-яке відхилення від оборотного циклу 1-2-3-4 буде джерелом необоротних втрат, що в зворотному циклі призведе до збільшення роботи циклу.

Роздивимося деякі характеристики циклу Лоренца. Під час аналізу будемо припускати, що теплоємності в процесах теплообміну постійні. Введемо позначення с_4-1 – теплоємність у процесі 4-1; с_2-3 – теплоємність у процесі 2-3; ; ; ; .

У зв'язку з тим, що зміни ентропії в процесах 2-3 і 4-1, рівні, тобто і , отримаємо , звідки , тоді:

. (3.30)

З урахуванням цього співвідношення холодильний і опалювальний коефіцієнти циклу Лоренца можуть бути записані:

;

. (3.31)

формули (3.31) справедливі для будь-яких оборотних циклів Лоренца незалежно від властивостей робочих речовин. Єдине обмеження стосується сталості теплоємності в процесах підведення і відведення теплоти.

Порівняємо між собою ефективність охолодження середовища від температури T₂ до T₁ за допомогою оборотного циклу Лоренца і за допомогою циклу Карно, у якому теплота від джерела, що охолоджується відводиться при температурі рівній найнижчій температурі циклу Лоренца. Будемо вважати, що передавання теплоти навколишньому середовищу в обох циклах відбувається при постійній температурі. На рис.3.10. у діаграмі T-s зображені трикутний цикл Лоренца 1-2-3-1, і цикл Карно 1-4-5-3-1, які мають однакову холодопродуктивність. З рисунка очевидно, що робота, затрачена в циклі Лоренца, менша, ніж у циклі Карно (пл.1-2-3-1 < пл.4-5-3-1). Скориставшись (3.30) та (3.31) отримаємо

, (3.32)

де , – холодильні коефіцієнти циклу Карно і трикутного циклу Лоренца.

Очевидно, що при ; при . Отже, при охолодженні тіл у процесах із постійною теплоємністю ефективність циклу Лоренца не менше, ніж удвічі перевершує ефективність циклу Карно.

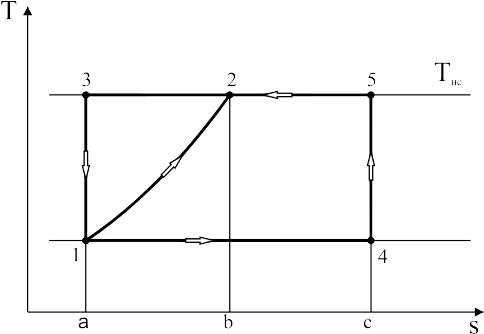
Рис.3.10. Порівняння трикутного циклу Лоренца і циклу Карно

На рис.3.11. показана залежність , що показує, що застосування трикутного циклу доцільно при будь-яких значеннях , хоча найбільша енергетична перевага досягається при малих значеннях. Природно, що економія енергії буде мати місце лише при охолодженні, а не у випадку необхідності підтримувати низьку температуру на постійному рівні.

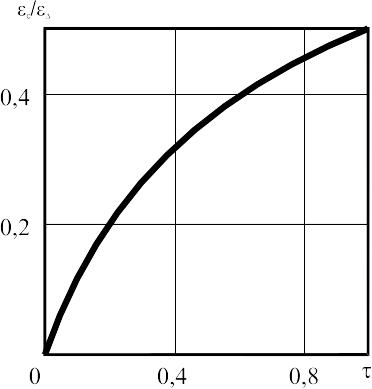
Рис.3.11. Порівняння холодильних коефіцієнтів “трикутного” циклу Лоренца та циклу Карно при охолодженні