3.5. Другий закон термодинаміки. Оцінка необоротних втрат зворотних циклів

Розглядаючи умови переходу теплоти від холодного тіла до більш теплого, Р.Клаузіус сформулював другий закон термодинаміки так: «Теплота не може переходити від холодного до теплого тіла сама собою, без компенсації». У цьому формулюванні підкреслюється необхідність витрати роботи для перенесення теплоти від холодного тіла до теплого (від джерела низької температури до навколишнього середовища або до джерела високої температури), тобто для здійснення зворотного кругового циклу необхідно мати як мінімум два джерела - низької та високої температури (навколишнього середовища) і при цьому необхідно затратити роботу або теплоту. На другому законі термодинаміки базується вся термодинамічна теорія холодильних машин.

Холодильні цикли реальних машин, на відміну від теоретичних, супроводжуються значними необоротними втратами, величина яких визначається умовами проведення процесів циклу. Усі без винятку процеси, що відбуваються в елементах холодильної машини, що здійснює зворотний круговий процес, є необоротними внутрішньо та зовнішньо. Проте під час термодинамічного аналізу можна усі або частину процесів вважати оборотними. При такому аналізі процесів, які відбуваються у різноманітних елементах холодильних машин дуже плідним є метод нарощування (підсумовування) втрат.

Для визначення розміру цих втрат використовується рівняння Гюї-Стодоли. На підставі першого і другого законів термодинаміки для зворотних циклів рівняння Гюї-Стодоли має вигляд

, (3.13)

де – збільшення роботи циклу, викликане необоротністю процесів; – сумарне збільшення ентропії всіх тіл, що приймають участь у процесах.

Оскільки ентропія – функція стану тіла, то в замкнутому зворотному циклі, ентропія робочої речовини змінюючись у процесах, в кінці повернеться до початкового стану, а зміна ентропії буде рівною нулю: . Отже, під s при здійсненні зворотного циклу варто розуміти зміну ентропії джерел теплоти. Оцінювати необоротні втрати в циклах з використанням рівняння Гюї-Стодоли можливо лише у випадку рівності холодопродуктивностей даного необоротного та еталонного оборотного (внутрішньо і зовнішньо) циклів. Такі оборотні цикли часто називають циклами з мінімальною роботою або циклами-зразками.

Для процесів, що відбуваються в тепловому насосі, рівняння Гюї-Стодоли справедливо в тому випадку, коли порівнюються цикли, що передають гарячому джерелу однакову кількість теплоти.

В зворотних циклах основними необоротними втратами є втрати, пов’язані з теплообміном між робочою речовиною та джерелами теплоти (зовнішня необоротність) та втрати пов’язані з дроселюванням (розширенням) та стисканням робочої речовини (внутрішня необоротність). Ефективним шляхом при визначенні необоротних втрат циклів є шлях окремого розгляду складових, що їх складають, з подальшим сумуванням і визначенням ступеня термодинамічної досконалості.

Розглянемо необоротні втрати, що виникають в циклах при використанні їх для охолодженні тіл. Припустимо, що необхідно охолодити якесь тіло (для нашого випадку воно буде джерелом низької температури) від температури Т_а до температури Т_b (рис.3.5). Найкращим циклом для такого охолодження буде цикл а-с-d-b, який складається з повністю оборотних процесів: адіабатних стискання a-c та розширення d-b, а також процесів теплообміну за відсутності різниці температур між робочою речовиною та джерелами теплоти c-d та b-a. Робота такого циклу буде найменшою з можливих. Будемо називати її мінімальною роботою циклу.

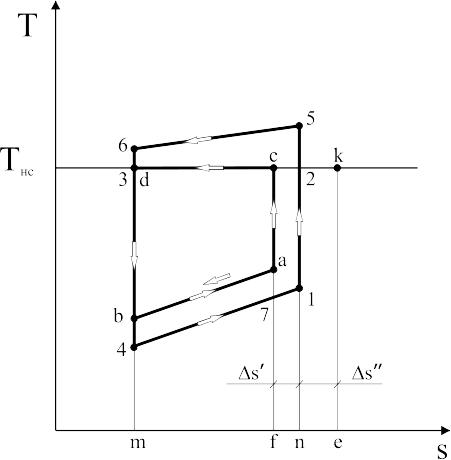
Рис.3.5. Зворотні цикли при кінцевій різниці температур у Т-s діаграмі

Таке ж охолодження можна здійснити за допомогою циклу 1-2-3-4. У цьому циклі теплота від робочої речовини передається до навколишнього середовища в процесі 2-3 при нескінченно малій різниці температур. Процеси стискання і розширення робочої речовини

1-2 і 3-4 відбуваються за постійної ентропії (s=const), тобто також оборотні. Таким чином, у цьому циклі є тільки один вид необоротності – теплообмін між тілом та робочою речовиною при кінцевій різниці температур у процесі 4-1. Процес а-b на діаграмі T-s показано умовно. Цикл 1-2-3-4 побудовано так, щоб його питома холодопродуктивність q₀ дорівнювала кількості теплоти, що відводиться від тіла (джерела низької температури), а саме,

пл.f-a-b-m = пл.n-1-4-m.

З вище сказаного відомо, що робота циклу 1-2-3-4 еквівалентна його площі 1-2-3-4 на діаграмі T-s. Порівняємо роботу, витрачену в циклах 1-2-3-4 та a-c-d-b. Питома холодопродуктивність циклу-зразка а-с-d-b і циклу 1-2-3-4 рівні між собою за умовами побудови циклу 1-2-3-4. Робота циклу зразка відповідає площі а-с-d-b. Як видно з побудови, робота, що витрачається в циклі з необоротністю в процесі теплообміну буде більшою від роботи циклу-зразка на величину :

~пл.1-2-3-4-пл.a-c-d-b або ~пл.1-2-с-a-b-4-1 . (3.14)

Оскільки пл.f-a-b-m = пл.n-1-4-m, то пл.7-a-b-4 = пл.n-1-7-f, тоді:

~пл.n-2-c-f = . (3.15)

Таким чином, збільшення роботи через необоротність у процесі теплообміну джерела низької температури і робочої речовини дорівнює зміні ентропії системи робоча речовина-джерело низької температури s', помноженому на температуру навколишнього середовища Т_нс. Зміна ентропії: , де – зміна ентропії джерела низької температури в процесі а—b; – зміна ентропії робочої речовини в процесі 4-1,

, (3.16)

, (3.17)

де і – теплоємність робочої речовини і джерела рахуємо постійними.

В реальних холодильних машинах процес відведення теплоти від робочої речовини до навколишнього середовища також проходить при кінцевій різниці температур – з’являється ще одна зовнішня необоротність. В цьому випадку холодильна машина буде працювати за циклом 1-5-6-4, тобто. Ця додаткова необоротність збільшить роботу циклу на величину ~пл.2-5-6-3.

Визначимо цю додаткову роботу. Кількість теплоти, відданої робочою речовиною в навколишнє середовище, відповідає пл.n-5-6-m. З іншого боку, навколишнє середовище прийняло таку ж кількість теплоти, величина якої еквівалентна площі е-3-k-m. Точка k на діаграмі ставиться таким чином, щоб пл.n-5-6-m = пл.e-k-3-m. Тоді

~пл.2-5-6-3 = пл.e-k-2-n = . (3.18)

Зміна ентропії s'' визначається аналогічно s': ,де – зміна ентропії навколишнього середовища; – зміна ентропії робочої речовини,

, (3.19)

. (3.20)

Загальна зміна ентропії викликана необоротними втратами в процесах теплообміну дорівнює: , а загальне збільшення роботи: .

Таким чином, робота циклу 1-5-6-4 може бути записана в такому вигляді:

w~пл.1-5-6-4 = пл.а-с-d-b+ = . (3.21)

Термодинамічна досконалість реальних циклів може бути оцінена коефіцієнтом оборотності _обр:

. (3.22)

З останньої рівності робимо висновок, що ефективність циклу досягає максимального значення у випадку рівності нулю необоротних втрат циклу, і зменшується при зростанні останніх.

Розглянемо, яким чином вплине на зростання необоротних втрат циклу заміна процесу адіабатного розширення робочої речовини дроселюванням. Для цього використаємо цикл зображений на рис.3.6., у T-s діаграмі, який має лише один необоротний процес – дроселювання. Процес дроселювання 3-4 зображено по лінії h=const. Інші процеси цього циклу повністю оборотні.

Робота циклу 1-2-3-4 еквівалентна площі 1-2-3-0-1. Циклом-зразком для нього буде цикл 1-2-5-4, що внутрішньо і зовнішньо оборотний, а його питома холодопродуктивність

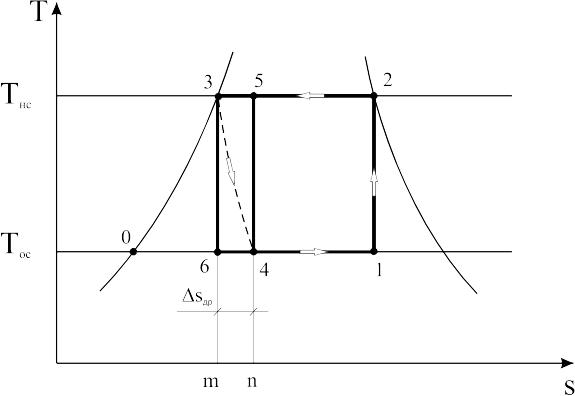
Рис.3.6. Зворотний цикл з дроселюванням в Т-s діаграмі

дорівнює питомої холодопродуктивності циклу 1-2-3-4. Робота циклу 1-2-5-4 еквівалентна площі 1-2-5-4. Величину додатково затраченої роботи викликаної дроселюванням знаходимо різницю площ:

~пл.1-2-3-0-1– пл.1-2-5-4 = пл.4-5-3-0-4. (3.23)

Робоча речовина в т.3 має запас потенціальної енергії, величина якої еквівалентна пл.6-3-0. У процесі дроселювання ця енергія переходить у кінетичну енергію струменя робочої речовини, що рухається, яка за дроселем перетворюється, через гальмування, в теплоту тертя і підводиться до самої робочої речовини. Ця теплота еквівалентна пл.n-4-6-m. Отже, відповідно до закону збереження енергії пл.6-3-0 = пл.n-4-6-m. Тоді

~пл.1-2-3-0-1 = пл.1-2-5-4+ пл.4-5-3-0-4 = пл.1-2-5-4+ пл.n-5-3-m = , (3.24)

де .

На рис.3.7. показано цикл 1-2-3-4 компресорної холодильної машини з адіабатним процесом стискання. У цьому циклі присутні усі види розглянутих раніше необоротних втрат – необоротні втрати, пов’язані з теплообміном робочої речовини і джерел, а також втрати, пов’язані з дроселюванням.

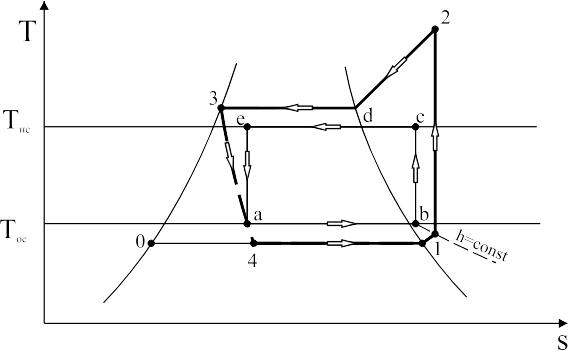
Рис.3.7. Необоротні втрати дійсного зворотного циклу

Для того щоб визначити ступінь термодинамічної досконалості циклу 1-2-3-4 і знайти коефіцієнт оборотності _обр, необхідно побудувати цикл-зразок. Цикл-зразок для аналізованого циклу будуємо так. Оскільки теплообмін між робочою речовиною та джерелами теплоти в циклі-зразку повинний проходити за нескінченно малої різниці температур, то він обмежується лініями T_ос і Т_нс. Точка а ставиться на перетинанні ліній 3-4 і T_ос. Потім через точку 1 проводиться лінія h=const до перетину з лінією T_ос (точка b). Таким чином, основою циклу-зразка є відрізок а-b. Так як h₁-h₄=h_b-h_a, то холодопродуктивність обох циклів однакова і, відповідно, буде виконуватися умова порівнювання циклів. Решта процесів циклу зразка також цілком оборотні: b-с – ізоентропне стискання; с-d – ізотермічне охолодження пари та d-е – ізотермічна конденсація при нескінченно малій різниці температур, що супроводжується значним зменшення об’єму; е-а – адіабатне розширення. Робота циклу 1-2-3-4 відповідає пл.1-2-3-0-1, робота циклу-зразка – пл.b-с-d-е-а. Різниця цих двох площ і буде додатковим збільшенням роботи реального циклу, який внутрішньо і зовнішньо необоротний