2. Найти предел функции:

а) в точке

б) на бесконечности

а) lim х² – 1 б) lim 5х⁶ - 2х³ + 4

х→1 2х² - х - 1 х→∞ 10х⁶ + 7х⁵ - 3х

3. Найти dy, если:

у = sin x ∙ 2cos³ x

4. Найти:

а) 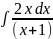б) (х³ + cos x - ) dx

5. Найти площадь фигуры, ограниченной линиями:

у = 3х²; х = 1; у = 0

Сделать чертеж.

Вариант 8.

1. Решить системы линейных уравнений:

а) по формуле Крамера

б) с помощью определителей II порядка с графической проверкой

а) б)

2. Найти предел функции:

а) в точке

б) на бесконечности

а) lim 5 х² + 4х– 1 б) lim 12х⁵ - 6х³ + 3х²

х→ -1 х² - 1 х→∞ 2х⁵ + 4х³

3. Найти dy, если:

у = е^{х + 5х}

4. Найти:

а) б) х⁴ + – е^х dx

5. Найти площадь фигуры, ограниченной линиями:

у = - х² + 4; х = 0; у = 0

Сделать чертеж.

Вариант 9.

1. Решить системы линейных уравнений:

а) по формуле Крамера

б) с помощью определителей II порядка с графической проверкой

а) б)

2. Найти предел функции:

а) в точке

б) на бесконечности

а) lim х² – 2х - 3 б) lim 2х⁶ - 3х + 2

х→3 х² - 5х + 6 х→∞ 12х⁶ + 4х³ - 5х²

3. Найти dy, если:

у = sin² x (х⁴ – 5х)

4. Найти:

а) х² ∙ √3х³ + 8dx б)

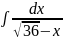
5. Найти площадь фигуры, ограниченной линиями:

у = х³; х₁ = 0; х₂ = 2; у = 0.

Сделать чертеж.

Экзаменационные вопросы

по математике (заочное отделение).

1. Системы линейных уравнений. Решение систем линейных уравнений по формулам Крамера.

2. Формулы Крамера в развернутом и свернутом виде. Исследование формул Крамера.

3. Определители II порядка. Основные свойства определителей.

4. Применение определителей II порядка для решения систем линейных уравнений.

5. Предел функции в точке. Условие существования предела функции. Правила определения предела функции в точке.

6. Предел функции в точке. Теоремы о пределах.

7. Бесконечно большие и бесконечно малые величины. Предел функции на бесконечности.

8. Предел функции на бесконечности. Правила определения предела функции на бесконечности.

9. Дифференциал функции. Правила определения дифференциала.

10. Первообразная. Неопределенный интеграл.

11. Таблицы неопределенных интегралов.

12. Метод непосредственного интегрирования.

13. Метод подстановки в неопределенных интегралах.

14. Определенный интеграл.

15. Формула Ньютона – Лейбница.

16. Вычисление площадей плоских фигур с помощью определенного интеграла.

Рекомендуемая литература.

Богомолов Н.В. Математика СПО;

Яковлев Г.Н. Математика для техникумов «Алгебра и начала анализа».