Департамент образования Кировской области
Кировское областное государственное образовательное бюджетное учреждение среднего профессионального образования
«Суводский лесхоз-техникум» математика
Методические указания и контрольные задания
для студентов – заочников по специальности 250109
«Садово-парковое и ландшафтное строительство»
г. Советск
2012 год.
ОДОБРЕНЫ Предметной (цикловой) методической комиссией (ОГСЭЕН и ФМ дисциплин)
Председатель _________________ Христолюбова Г.Н. «____» ________________ 20 ___ г. |
Составлены в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускника по специальности 250109 «Садово-парковое и ландшафтное строительство»
Методист заочного отделения: _________________ Мосунова Е.Ф. |
АВТОР: преподаватель КОГОБУ СПО «Суводский лесхоз-техникум»
Светлакова Е.А.
Рецензент: преподаватель КОГОБУ СПО «Суводский лесхоз-техникум»
Лобанов А.И.
Пояснительная записка
Для успешной сдачи экзамена по математике и выполнения контрольной работы необходимо изучить следующие главы учебника Богомолова Н.В. «Математика» для средних специальных учебных заведений.
I задание. Системы линейных уравнений. Глава I, §7.
II задание. Теория Пределов. Глава IV.
III задание. Дифференциал функции, приложение дифференциала.
Глава VII, § 60.
IV задание. Неопределенный интеграл. Глава VIII.
V задание. Определенный интеграл. Глава IX.
Вариант 1.
1. Решить системы линейных уравнений:
а) по формуле Крамера с графической проверкой
б) с помощью определителей II порядка с графической проверкой
а)
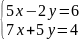б)
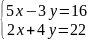
2. Найти предел функции:
а) в точке
б) на бесконечности
а) lim х2 – 2х – 3 б) lim 25х4 – 2х3 – 4
х→3 х2 – 5х + 6 х→∞ 5х4 + 6х
3. Найти dy, если:
у = sin х + х3 – 2
4. Найти:
а)
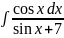б)
(х2
– 3х + 2) dx
5. Найти площадь фигуры, ограниченной линиями:
у = х2; у = 3 – 2х
Сделать чертеж.
Вариант 2.
1. Решить системы линейных уравнений:
а) по формуле Крамера
б) с помощью определителей II порядка с графической проверкой
а)
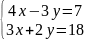б)
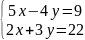
2. Найти предел функции:
а) в точке
б) на бесконечности
а) lim х2 – 3х + 2 б) lim 36х5 – 8х3 + 2
х→1 х2 – 4х + 3 х→∞ 6х5 + 12х2
3. Найти dy, если:
у = (х2 + 1)(2 + х4)
4. Найти:
а)
х√
х2
+ 1dx
б)
(х2
+ sin
x
-
)
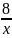dx
5. Найти путь, пройденный телом от начала движения за 3 секунды, если;
ν (t) = 3t – tа
Вариант 3.