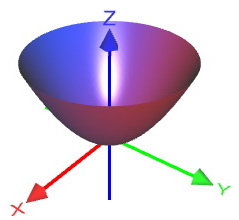
Эллиптический параболоид
Каноничный эллиптический параболоид
в прямоугольной системе задаётся
уравнением 
.
Данная поверхность выглядит бесконечной
чашей:
Название
«эллиптический параболоид» тоже
произошло из результатов исследования
сечений. В горизонтальных сечениях
плоскостями 
получаются
различные эллипсы:
,
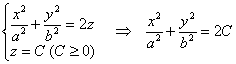в частности, при
эллипс вырождается в
точку (начало координат), которая
называется вершиной эллиптического
параболоида.
А вертикальные сечения плоскостями,
параллельными оси
,
представляют собой различные параболы.
Например, сечение координатной
плоскостью
:
–
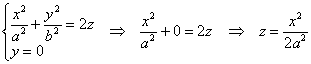парабола, лежащая в плоскости
.
Или
сечение плоскостью
:
–
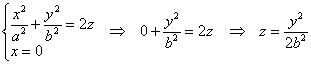парабола, лежащая в плоскости
.
Отсюда и эллиптический параболоид.
На практике обычно встречается упрощенная
версия поверхности с горизонтальными
сечениями-окружностями.
Перепишем каноническое уравнение в
прикладном функциональном виде:
–
характерным признаком функции, как и в
ситуации с конусом, является равенство
коэффициентов при 
.
Пример 18
Построить поверхность 
.
Записать неравенства, определяющие
внутреннюю и внешнюю часть эллиптического
параболоида.
Решение:
используем ту же методику, что и при
построении конической поверхности.
Рассмотрим какое-нибудь не очень большое
значение «зет», здесь удобно выбрать 
,
и найдём сечение эллиптического
параболоида этой плоскостью:
–
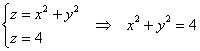окружность радиуса 2.
Теперь на высоте
изобразим
данную окружность и аккуратно соединим
её с вершиной (началом координат) двумя
параболами. В результате получится
такая вот симпатичная
чашка:
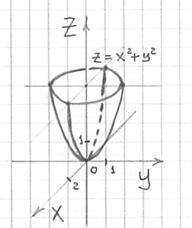Рассматриваемый
частный случай параболоида с горизонтальными
сечениями-окружностями также
называют параболоидом вращения,
поскольку его можно получить вращением
параболы вокруг оси
С неравенствами ничего нового. Нетрудно
догадаться, что неравенство 
или,
если развернуть запись в более привычном
порядке, 
определяет
множество точек внутри чаши (т.к.
неравенство строгое, то сама поверхность
не входит в решение). И, соответственно,
неравенство 
задаёт
множество внешних точек.
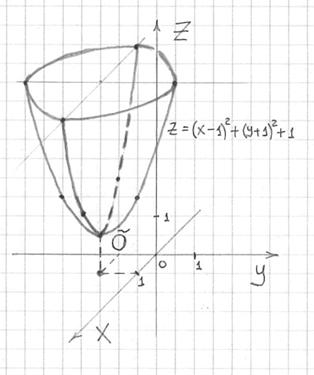
По моим наблюдениям, на практике часто
встречается эллиптический параболоид
вида 
,
который выглядит точно так же, но
мигрировал вершиной в точку 
.
Именно такую поверхность мы исследовали
с помощью линий
уровня в Примере №14
первого урока темы.
Ещё один типичное расположение эллиптического параболоида:
Пример 19
Построить поверхность 
Решение: если коэффициенты
при
отрицательны
(сразу оба), то чаша параболоида «смотрит
вниз». Вершина поверхности расположена
в точке 
.
Это понятно не только интуитивно, но и
подкрепляется простым аналитическим
рассуждением: очевидно, что рассмотрев
любую другую пару значений 
мы
уменьшим функцию
.
Таким образом, точка
–
это максимум функции двух
переменных, коим в данном случае
и является вершина параболоида.
В целях построения поверхность удобно
«отсечь» плоскостью
.
Сечение представляет собой:
–
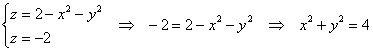окружность радиуса 2.
Выполним чертёж:
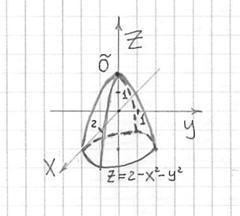Готово.
Заключительное задание для самостоятельного решения:
Пример 20
Построить эллиптический параболоид 
Чертёж в конце урока, который приблизился к своему завершению.
Среди поверхностей 2-го порядка за кадром остались редко встречающиеся на практике:
( ниже перечислены канонические уравнения, в которых – положительные числа)
–
гиперболический параболоид («седло»);
–
однополостной гиперболоид;
–
двуполостной гиперболоид.
Более подробную информацию об этих поверхностях можно почерпнуть в учебнике аналитической геометрии либо другом источнике информации. Если возникнет необходимость выполнить их построение – используйте метод сечений, он действительно прост и эффективен!
Я бы с радостью всё рассказал, но, во-первых, это нецелесообразно с практической точки зрения, а во-вторых, размер статьи подходит к той опасной грани, после которой посетители сайта будут считать автора не только фанатом, но и начнут всерьёз опасаться за его здоровье. Впрочем, санитары разрешили мне закончить данный абзац =)
А если серьёзно, то этой статьи я опасался чуть ли не с первых дней создания сайта ввиду большого объема работы. Но вот, наконец, клуб любителей функций 2-х переменныхшироко распахнул двери, и теперь-то уж мы с вами оттянемся в полный рост =)
Обязательно приходите!
Решения и чертежи:
Пример 1: Решение:
выполним чертёж:
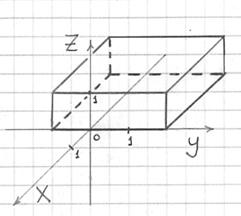Данное
тело определяется системой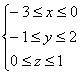 
Пример 3: Решение:
а) Сначала удобно построить прямую 
,
лежащую в плоскости
.
Используем начало координат, и, например,
точку 
.
б) Сначала удобно построить прямую 
,
лежащую в плоскости
.
Используем начало координат, и, например,
точку 
.
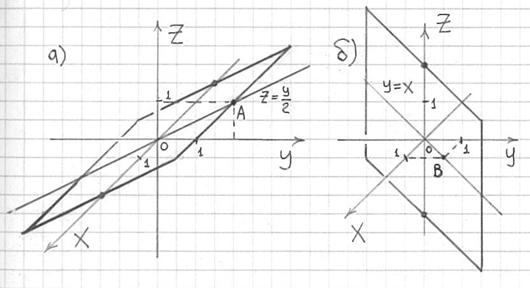
Пример 6: Решение:
запишем уравнение плоскости в
отрезках:
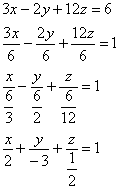Выполним
чертёж:
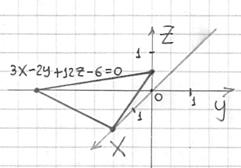
Пример 10: Решение:
функция
задаёт
верхнюю часть цилиндра 
:
Проекция
на плоскость
:
часть данной плоскости, ограниченная
«плоскими» прямыми 
(включая
прямые).
Проекция на плоскость
:
часть данной плоскости, ограниченная
прямыми 
(
–
любое), включая сами прямые.
Проекция
на плоскость
:
полуокружность 
Пример 12: Чертежи:
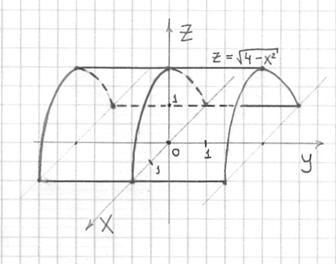
Пример 13: Решение:
данный эллипсоид получен вращением
эллипса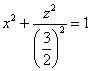 
(плоскость
)
вокруг оси
:
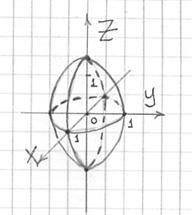Примечание:
также можно считать, что вращается
эллипс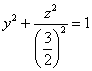 
,
лежащий в плоскости
.
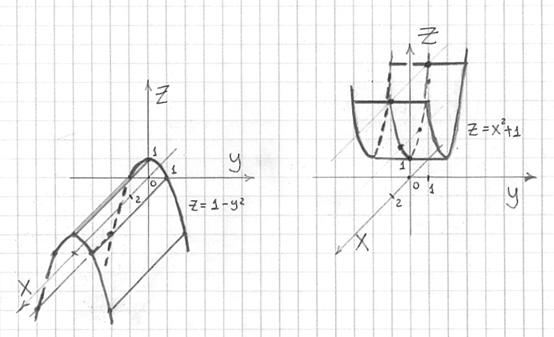
Пример 15: Решение:
областью определения данной функции
является круг
с
центром в начале координат радиуса
.
Функция
задаёт
полусферу, лежащую в верхнем
полупространстве, с центром в начале
координат радиуса
:
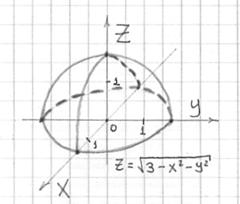
Пример 17: Решение:
сечения конуса плоскостями
представляют
собой окружности 
.
Выполним чертёж:
Неравенство 
задаёт
множество точек, находящихся внутри
конуса; неравенство 
задаёт
множество внешних точек.
Пример 20: Решение:
вершина параболоида находится в точке 
.
Выполним чертёж:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)