Параболические цилиндры

Как следует из названия, направляющей такого цилиндра является парабола.

Пример 11

Построить поверхность   и найти её проекции на координатные плоскости.

Не мог удержаться от этого примера =)

Решение: идём проторенной тропой. Перепишем уравнение в виде  , из которого следует, что «зет» может принимать любые значения. Зафиксируем   и построим обычную параболу   на плоскости  , предварительно отметив тривиальные опорные точки  . Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости)   и аккуратно соединяем их параллельными прямыми (образующими цилиндра): 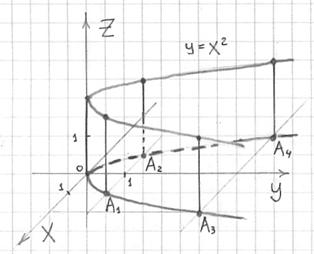 Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.

Проекции.

1) Проекцией цилиндра на плоскость   является парабола  . Следует отметить, что в данном случае нельзя рассуждать об области определения функции 2-х переменных – по той причине, что уравнение цилиндра   не приводимо к функциональному виду  .

2) Проекция цилиндра на плоскость   представляет собой полуплоскость  , включая ось  3) И, наконец, проекцией цилиндра на плоскость   является вся плоскость  .

Пример 12

Построить параболические цилиндры:

а)  , ограничиться фрагментом поверхности в ближнем полупространстве;

б)   на промежутке 

В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину. Я и сам особо не заморачиваюсь над красотой линий, если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа ;-)

Гиперболические цилиндры

Направляющими таких цилиндров являются гиперболы. Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, чем предыдущие виды, поэтому я ограничусь единственным схематическим чертежом гиперболического цилиндра  : 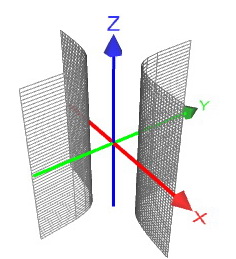Принцип рассуждения здесь точно такой же – обычная школьная гипербола   из плоскости   непрерывно «размножается» вверх и вниз до бесконечности.

Рассмотренные цилиндры относятся к так называемым поверхностям 2-го порядка, и сейчас мы продолжим знакомиться с другими представителями этой группы:

Эллипсоид. Сфера и шар

Каноническое уравнение эллипсоида в прямоугольной системе координат имеет вид  , где   – положительные числа (полуоси эллипсоида), которые в общем случае  различны. Эллипсоидом называют как поверхность, так и тело, ограниченное данной поверхностью. Тело, как многие догадались, задаётся неравенством   и координаты любой внутренней точки (а также любой точки поверхности) обязательно удовлетворяют этому неравенству. Конструкция симметрична относительно координатных осей и координатных плоскостей: 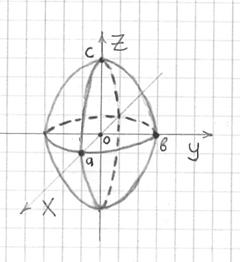Происхождение термина «эллипсоид» тоже очевидно: если поверхность «разрезать» координатными плоскостями, то в сечениях получатся три различных (в общем случае)эллипса. В зависимости от значений   эллипсоид может быть вытянут вдоль любой оси, причём вытянут достаточно далеко.

Если две полуоси совпадают, то данную поверхность/тело называют эллипсоидом вращения. Так, например, эллипсоид   получен вращением эллипса   вокруг оси   (представьте мысленно).

Небольшая задачка для самостоятельного решения:

Пример 13

Построить эллипсоид  . Записать уравнение порождающего эллипса и ось, вокруг которой осуществляется его вращение.

Чертёж и краткий комментарий в конце урока.

В случае равенства всех полуосей  , эллипсоид вырождается в сферу:   – данное уравнение задаёт сферу с центром в начале координат радиуса  .

Тело, ограниченное сферой, называется шаром. Неравенство   определяет шар с центром в начале координат радиуса  . И, соответственно, противоположному условию  удовлетворяют координаты любой внешней точки.

Разделаемся с аппетитным Колобком:

Пример 14

Построить поверхность  . Найти функции, задающие верхнюю и нижнюю полусферу, указать их области определения. Записать аналитическое выражение шара, ограниченного данной сферой и проверить, принадлежат ли ему точки 

Решение: уравнение   задаёт сферу с центром в начале координат радиуса 2.  Здесь, как и в примерах с параболическими цилиндрами, выгодно уменьшить масштаб чертежа: 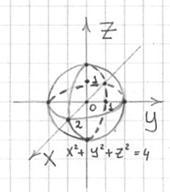Выразим «зет»:  – функция, задающая верхнюю полусферу;  – функция, задающая нижнюю полусферу.

Областью определения каждой функции является круг   с центром в начале координат радиуса 2 (проекция полусфер на плоскость  ).

Неравенство   определяет шар с центром в начале координат радиуса 2. Подставим координаты точек   в данное неравенство:

1) 

Получено неверное неравенство, следовательно, точка «дэ» лежит вне шара.

2) 

Получено верное неравенство, значит, точка «эф» принадлежит шару, а конкретнее – его границе (сфере).

Материал о сферах и шарах достаточно прост, и я предлагаю вам чисто символическое задание для самостоятельного решения:

Пример 15

Найти область определения функции 2-х переменных   и построить соответствующую поверхность. Краткое решение и чертёж в конце урока.

Кстати, наша планета, кто не знает, чуть-чуть, но таки не шар.