Уравнение плоскости в отрезках

Важнейшая прикладная разновидность. Если все коэффициенты общего уравнения плоскости   отличны от нуля, то оно представимо в виде  , который называется уравнением плоскости в отрезках. Очевидно, что плоскость пересекает координатные оси в точках  , и большое преимущество такого уравнения состоит в лёгкости построения чертежа:

Пример 5

Построить плоскость 

Решение: сначала составим уравнение плоскости в отрезках. Перебросим свободный член направо и разделим обе части на 12:

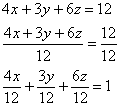
Делаем дроби трёхэтажными:

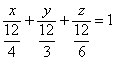
Именно так! – ведь знаменатели могут оказаться и дробными. Но в данном случае всё разделилось нацело:

Таким образом, плоскость проходит через точки  . В целях  самоконтроля координаты каждой точки устно подставим в исходное уравнение  . После чего выполним чертёж: 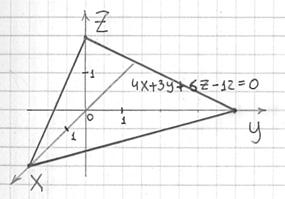В отличие от предыдущих примеров здесь фрагмент плоскости изображается в виде треугольника, который в общем случае может «прорисоваться» в любом из 8-ми октантов.

Задание для тренировки:

Пример 6

Построить плоскость 

Краткое решение и чертёж в конце урока.

Переходим к другой обширной группе обитателей 3D-мира:

Цилиндрические поверхности

Или, если короче – цилиндры.

! Примечание: в ряде источников информации под цилиндром понимается исключительно геометрическое тело, а не поверхность!

Следует отметить, что в математике под этими терминами скрывается не совсем то, что обычно подразумевает обыватель, и класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:

Пример 7

Построить поверхность, заданную уравнением 

…что за дела? Не опечатка ли здесь? Вроде как дано каноническое уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что недавно использовали для плоскостей. Перепишем уравнение в виде  , из которого следует, что «зет» принимаетлюбые значения. Зафиксируем   и построим в плоскости   эллипс  . Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз. Легко понять, что поверхность бесконечна: 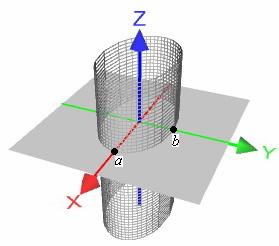Данная поверхность называется эллиптическим цилиндром. Эллипс   (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют). Ось   является осью симметрии поверхности (но не её частью!).

Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению  .

Пространственное неравенство   задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство   определяет множество точек вне цилиндра.

В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:

Пример 8

Построить поверхность, заданную уравнением 

Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса   в плоскости  , а затем ещё пару окружностей сверху и снизу. Полученные окружности (направляющие цилиндра) аккуратно соединяем четырьмя параллельными прямыми (образующими цилиндра): Не забываем использовать пунктир для невидимых нам линий.

Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению  . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству  , а неравенство   задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.

Пример 9

Построить поверхность   и найти её проекцию на плоскость 

Перепишем уравнение в виде   из которого следует, что «икс» принимаетлюбые значения. Зафиксируем   и в плоскости   изобразим окружность   – с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает всезначения, то построенная окружность порождает круговой цилиндр с осью симметрии  . Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон: 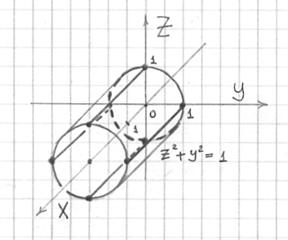На этот раз я ограничился кусочком цилиндра на промежутке   и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.

Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.

Теперь разбираемся с проекцией цилиндра на плоскость  . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку. Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси   смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость  . А кажется он бесконечной полосой, заключенным между прямыми  , включая сами прямые. Данная проекция – это в точности область определения функций   (верхний «жёлоб» цилиндра),   (нижний «жёлоб»).

Давайте, кстати, проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси  . Тенью (проекцией) цилиндра на плоскость   является аналогичная бесконечная полоса – часть плоскости  , ограниченная прямыми   (  – любое), включая сами прямые.

А вот проекция на плоскость   несколько иная. Если смотреть на цилиндр из острия оси  , то он спроецируется в окружность единичного радиуса  , с которой мы начинали построение.

Пример 10

Построить поверхность   и найти её проекции на координатные плоскости

Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат; выясните, какую именно часть цилиндра задаёт функция  . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце урока.

Эллиптические и другие цилиндрические поверхности могут быть смещены относительно координатных осей, например:

 (по знакомым мотивам статьи о линиях 2-го порядка) –  цилиндр единичного радиуса с линией симметрии, проходящей через точку   параллельно оси  . Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.