Распространенные уравнения плоскостей
Типовые варианты расположения плоскостей в прямоугольной системе координат детально рассмотрены в самом начале статьи Уравнение плоскости. Тем не менее, ещё раз остановимся на уравнениях, которые имеют огромное значение для практики.
Прежде всего, вы должны на полном автомате
узнавать уравнения плоскостей, которые
параллельны координатным плоскостям 
.
Фрагменты плоскостей стандартно
обозначают прямоугольниками, которые
в последних двух случаях выглядят, как
параллелограммы. По умолчанию размеры
можно выбрать любые (в разумных пределах,
конечно), при этом желательно, чтобы
точка, в которой координатная ось
«протыкает» плоскость являлась центром
симметрии:
Строго
говоря, координатные оси местами
следовало изобразить пунктиром, но во
избежание путаницы будем пренебрегать
данным нюансом.
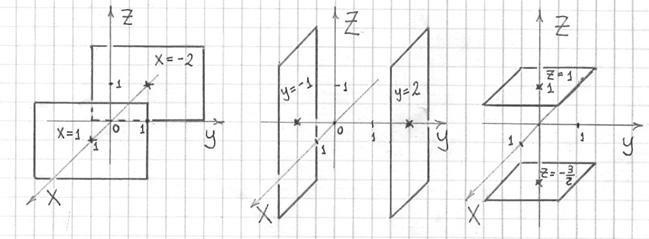
Тем, кто ещё не успел, настоятельно рекомендую ознакомиться с указанной выше статьёй и понять неформальный смысл этих уравнений. Повторим заодно и соответствующие неравенства:
– (левый чертёж) неравенство 
задаёт
дальнее от нас полупространство, исключая
саму плоскость 
;
– (средний чертёж) неравенство 
задаёт
правое полупространство, включая
плоскость 
;
– (правый чертёж) двойное
неравенство 
задаёт
«слой», расположенный между плоскостями 
,
включая обе плоскости.
Для самостоятельно разминки:
Пример 1
Изобразить тело, ограниченное
плоскостями 
Составить
систему неравенств, определяющих данное
тело.
Из-под грифеля вашего карандаша должен выйти старый знакомый прямоугольный параллелепипед. Не забывайте, что невидимые рёбра и грани нужно прочертить пунктиром. Готовый чертёж в конце урока.
Пожалуйста, НЕ ПРЕНЕБРЕГАЙТЕ учебными задачами, даже если они кажутся слишком простыми. А то может статься, раз пропустили, два пропустили, а затем потратили битый час, вымучивая трёхмерный чертёж в каком-нибудь реальном примере. Кроме того, механическая работа поможет гораздо эффективнее усвоить материал и развить интеллект! Не случайно в детском саду и начальной школе детей загружают рисованием, лепкой, конструкторами и другими заданиями на мелкую моторику пальцев.
Следующую группу плоскостей условно назовём «прямыми пропорциональностями» – это плоскости, проходящие через координатные оси:
1) уравнение вида 
(здесь
и далее 
) задаёт
плоскость, проходящую через ось
;
2) уравнение вида 
задаёт
плоскость, проходящую через ось 
;
3) уравнение вида 
задаёт
плоскость, проходящую через ось
.
Хотя формальный признак очевиден (какая переменная отсутствует в уравнении – через ту ось и проходит плоскость), всегда полезно понимать суть происходящих событий:
Пример 2
Построить плоскость 
Как лучше осуществить построение? Предлагаю следующий алгоритм:
Сначала перепишем уравнение в виде 
,
из которого хорошо видно, что «игрек»
может принимать любые значения.
Зафиксируем значение
,
то есть, будем рассматривать координатную
плоскость 
.
Уравнения 
задаютпространственную
прямую, лежащую в данной
координатной плоскости. Изобразим эту
линию на чертеже. Прямая проходит через
начало координат, поэтому для её
построения достаточно найти одну точку.
Пусть 
.
Откладываем точку 
и
проводим прямую.
Теперь возвращаемся к уравнению
плоскости
.
Поскольку «игрек» принимаетлюбые значения,
то построенная в плоскости
прямая
непрерывно «тиражируется» влево и
вправо. Именно так и образуется наша
плоскость
,
проходящая через ось
.
Чтобы завершить чертёж, слева и справа
от прямой
откладываем
две параллельные линии и поперечными
горизонтальными отрезками «замыкаем»
символический параллелограмм:
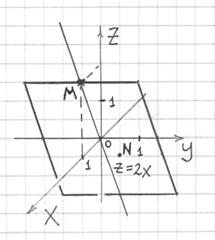Так
как условие не накладывало дополнительных
ограничений, то фрагмент плоскости
можно было изобразить чуть меньших или
чуть бОльших размеров.
Ещё раз повторим смысл пространственного
линейного неравенства на примере 
.
Как определить полупространство, которое
оно задаёт? Берём какую-нибудь точку, не
принадлежащую плоскости
,
например, точку 
из
ближнего к нам полупространства и
подставляем её координаты в неравенство:
Получено верное неравенство, значит, неравенство задаёт нижнее (относительно плоскости ) полупространство, при этом сама плоскость не входит в решение.
Пример 3
Построить плоскости
а) 
;
б) 
.
Это задания для самостоятельного построения, в случае затруднений используйте аналогичные рассуждения. Краткие указания и чертежи в конце урока.
На практике особенно распространены плоскости, параллельные оси . Частный случай, когда плоскость проходит через ось, только что был в пункте «бэ», и сейчас мы разберём более общую задачу:
Пример 4
Построить плоскость 
Решение: в уравнение в явном виде не участвует переменная «зет», а значит, плоскость параллельна оси аппликат. Применим ту же технику, что и в предыдущих примерах.
Перепишем уравнение плоскости в виде 
из
которого понятно, что «зет» может
принимать любые значения.
Зафиксируем
и
в «родной» плоскости
начертим
обычную «плоскую» прямую 
.
Для её построения удобно взять опорные
точки 
.
Поскольку «зет» принимает все значения,
то построенная прямая непрерывно
«размножается» вверх и вниз, образуя
тем самым искомую плоскость
.
Аккуратно оформляем параллелограмм
разумной величины:
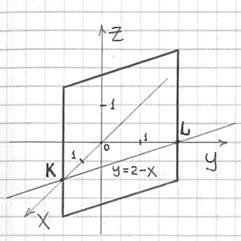Готово.