ФНП:

Область определения функции 2-х переменных. Линии уровня  Основные поверхности  Частные производные  Частные производные функции трёх переменных

Функция двух переменных. Область определения и линии уровня

До сих пор нами рассматривалась простейшая функциональная модель, в которой функция   зависит от единственного аргумента. Но при изучении различных явлений окружающего мира мы часто сталкиваемся с одновременным изменением более чем двух величин, и многие процессы можно эффективно формализовать функцией нескольких переменных  , где   – аргументы или независимые переменные.  Начнём разработку темы с наиболее распространенной на практике функции двух переменных  .

Функцией двух переменных называется закон, по которому каждой паре значенийнезависимых переменных   (аргументов) из области определения соответствует значение зависимой переменной   (функции).

Данную функцию обозначают следующим образом:

 либо  , или же другой стандартной буквой: 

Поскольку упорядоченная пара значений «икс» и «игрек» определяет точку на плоскости, то функцию также записывают через  , где   – точка плоскости   с координатами  . Такое обозначение широко используется в некоторых практических заданиях.

Геометрический смысл функции 2-х переменных очень прост. Если функции одной переменной   соответствует определённая линия на плоскости (например,    – всем знакомая школьная парабола), то график функции двух переменных   располагается в трёхмерном пространстве. На практике чаще всего приходится иметь дело споверхностью, но иногда график функции может представлять собой, например, пространственную прямую (ые) либо даже единственную точку.

С элементарным примером поверхности мы хорошо знакомы ещё из курса аналитической геометрии – это плоскость  . Предполагая что  , уравнение легко переписать в функциональном виде:

Важнейший атрибут функции 2-х переменных – это уже озвученная область определения.

Областью определения функции двух переменных   называется множествовсех пар  , для которых существует значение  .

Графически область определения представляет собой всю плоскость   либо её часть. Так, областью определения функции   является вся координатная плоскость   – по той причине, что для любой точки   существует значение  .

Но такое праздный расклад бывает, конечно же, не всегда:

Как найти область определения функции двух переменных?

Рассматривая различные понятия функции нескольких переменных, полезно проводить аналогии с соответствующими понятиями функции 1-ой переменной. В частности, при выяснении области определения   мы обращали особое внимание на те функции, в которых есть дроби, корни чётной степени, логарифмы и т. д. Здесь всё точно так же!

Задача на нахождение области определения функции двух переменных практически со 100-ной вероятностью встретится вам в тематической работе, поэтому я разберу приличное количество примеров:

Пример 1

Найти область определения функции 

Решение: так как знаменатель не может обращаться в ноль, то:

Ответ: вся координатная плоскость   кроме точек, принадлежащих прямой 

Да-да, ответ лучше записать именно в таком стиле. Область определения функции 2-х переменных редко обозначают каким-либо символом, гораздо чаще используют словесное описание и/или чертёж.

Если бы по условию требовалось выполнить чертёж, то следовало бы изобразить координатную плоскость   и пунктиром провести прямую  . Пунктир сигнализирует о том, что линия не входит в область определения.

Как мы увидим чуть позже, в более трудных примерах без чертежа и вовсе не обойтись.

Пример 2

Найти область определения функции 

Решение: подкоренное выражение должно быть неотрицательным: 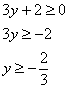Ответ: полуплоскость 

Графическое изображение здесь тоже примитивно: чертим декартову систему координат,сплошной линией проводим прямую   и штрихуем верхнюю полуплоскость. Сплошная линия указывает на тот факт, что она входит в область определения.

Внимание! Если вам ХОТЬ ЧТО-ТО не понятно по второму примеру, пожалуйста, подробно изучите/повторите урок Линейные неравенства – без него придётся очень туго!

Миниатюра для самостоятельного решения:

Пример 3

Найти область определения функции 

Двухстрочное решение и ответ в конце урока.

Продолжаем разминаться:

Пример 4 Найти область определения функции и изобразить её на чертеже

Решение: легко понять, что такая формулировка задачи требует выполнения чертёжа (даже если область определения очень проста). Но сначала аналитика: подкоренное выражением должно быть неотрицательным:   и, учитывая, что знаменатель не может обращаться в ноль, неравенство становится строгим: 

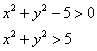
Как определить область, которую задаёт неравенство  ? Рекомендую тот же алгоритм действий, что и при решении линейных неравенств.

Сначала чертим линию, которую задаёт соответствующее равенство. Уравнение   определяет окружность с центром в начале координат радиуса  , которая делит координатную плоскость на две части – «внутренность» и «внешность» круга. Так как неравенство у нас строгое, то сама окружность заведомо не войдёт в область определения и поэтому её нужно провести пунктиром.

Теперь берём произвольную точку плоскости, не принадлежащую окружности  , и подставляем её координаты в неравенство  . Проще всего, конечно же, выбрать начало координат  :

Получено неверное неравенство, таким образом, точка   не удовлетворяетнеравенству  . Более того, данному неравенству не удовлетворяет и любая точка, лежащая внутри круга, и, стало быть, искомая область определения – внешняя его часть. Область определения традиционно штрихуется: 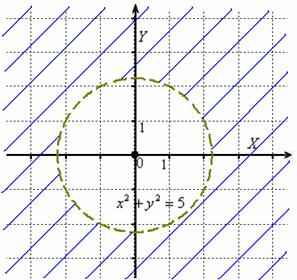Желающие могут взять любую точку, принадлежащую заштрихованной области и убедиться, что её координаты удовлетворяют неравенству  . Кстати, противоположное неравенство   задаёт круг с центром в начале координат, радиуса  .

Ответ: внешняя часть круга 

Вернёмся к геометрическому смыслу задачи: вот мы нашли область определения и заштриховали её, что это значит? Это значит, что в каждой точке   заштрихованной области существует значение «зет» и графически функция   представляет собой следующую поверхность: 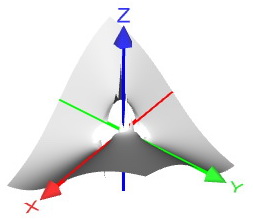На схематическом чертеже хорошо видно, что данная поверхность местами расположена надплоскостью   (ближний и дальний от нас октанты),  местами – под плоскостью   (левый и правый относительно нас октанты). Также поверхность проходит через оси  . Но поведение функции как таковое нам сейчас не очень интересно – важно, что всё это происходит исключительно в области определения. Если мы возьмём любую точку  , принадлежащую кругу   – то никакой поверхности там не будет (т.к. не существует «зет»), о чём и говорит круглый пробел в середине рисунка.

Пожалуйста, хорошо осмыслите разобранный пример, поскольку в нём я подробнейшим образом разъяснил саму суть задачи.

Следующее задание для самостоятельного решения:

Пример 5 Найти область определения функции и изобразить её на чертеже

Краткое решение и чертёж в конце урока. Вообще, в рассматриваемой теме среди линий 2-го порядка наиболее популярна именно окружность, но, как вариант, в задачу могут «затолкать» эллипс, гиперболу или параболу.

Идём на повышение:

Пример 6 Найти область определения функции 

Решение: подкоренное выражение должно быть неотрицательным:   и знаменатель не может равняться нулю:  . Таким образом, область определения задаётся системой  .

С первым условием разбираемся по стандартной схеме рассмотренной на уроке Линейные неравенства: чертим прямую   и определяем полуплоскость, которая соответствует неравенству  . Поскольку неравенство нестрогое, то сама прямая также будет являться решением.

Со вторым условием системы тоже всё просто: уравнение   задаёт ось ординат, и коль скоро  , то её следует исключить из области определения.

Выполним чертёж, не забывая, что сплошная линия обозначает её вхождение в область определения, а пунктир – исключение из этой области: 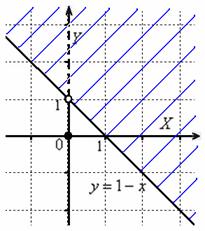Следует отметить, что здесь мы уже фактически вынуждены сделать чертёж. И такая ситуация типична – во многих задачах словесное описание области затруднено, а даже если и опишите, то, скорее всего, вас плохо поймут и заставят изобразить область.   

Ответ: область определения: 

К слову, такой ответ без чертежа действительно смотрится сыровато.

Ещё раз повторим геометрический смысл полученного результата: в заштрихованной области существует график функции  , который представляет собой поверхность трёхмерного пространства. Эта поверхность может располагаться выше/ниже плоскости  , может пересекать плоскость – в данном случае нам всё это параллельно. Важен сам факт существования поверхности, и важно правильно отыскать область, в которой она существует.

Пример 7 Найти область определения функции 

Это пример для самостоятельного решения. Примерный образец чистового оформления задачи в конце урока.

Не редкость, когда вроде бы простые на вид функции вызывают далеко не скороспелое решение:

Пример 8 Найти область определения функции 

Решение: используя формулу разности квадратов, разложим подкоренное выражение на множители:  .

Произведение двух множителей неотрицательно  , когда оба множителя неотрицательны:   ИЛИ когда оба неположительны:  . Это типовая фишка. Таким образом, нужно решить две системы линейных неравенств и ОБЪЕДИНИТЬполученные области. В похожей ситуации вместо стандартного алгоритма гораздо быстрее работает метод научного, а точнее, практического тыка =)

Чертим прямые  , которые разбивают координатную плоскость на 4 «уголка». Берём какую-нибудь точку, принадлежащую верхнему «уголку», например, точку   и подставляем её координаты в уравнения 1-ой системы:  . Получены верные неравенства, а значит, решением системы   является весь верхний «уголок». Штрихуем.

Теперь берём точку  , принадлежащую правому «уголку». Осталась 2-ая система, в которую мы и подставляем координаты этой точки:  . Второе неравенство неверно, следовательно, и весь «правый» уголок не является решением системы  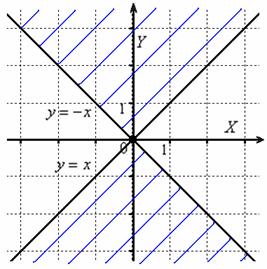. Аналогичная история с «левым» уголком, который тоже не войдёт в область определения.

И, наконец, подставляем во 2-ую систему координаты подопытной точки   нижнего «уголка»:  . Оба неравенства верны, а значит, решением системы   является и весь нижний «уголок», который тоже следует заштриховать.

В реальности так подробно расписывать, естественно, не надо – все закомментированные действия легко выполняются устно!

Ответ: область определения представляет собой объединение решений систем  .

Как вы догадываетесь, без чертежа такой ответ вряд ли пройдёт, и это обстоятельство вынуждает взять в руки линейку с карандашом, хоть того и не требовало условие.

А это ваш орешек:

Пример 9 Найти область определения функции 

Хороший студент всегда скучает по логарифмам:

Пример 10 Найти область определения функции 

Решение: аргумент логарифма строго положителен, поэтому область определения задаётся системой  .

Неравенство   указывает на правую полуплоскость и исключает ось  .

Со вторым условием ситуация более затейлива, но тоже прозрачна. Вспоминаем синусоиду. В качестве аргумента выступает «игрек», но это не должно смущать – игрек, так игрек, зю, так зю. Где синус больше нуля? Синус больше нуля, например, на интервале  . Поскольку функция периодична, то таких интервалов бесконечно много и в свёрнутом виде решение неравенства   запишется следующим образом: , где   – произвольное целое число.

Бесконечное количество промежутков, понятно, не изобразить, поэтому ограничимся интервалом    и его соседями:

Выполним чертёж, не забывая, что согласно первому условию, наше поле деятельности ограничивается строго правой полуплоскостью: 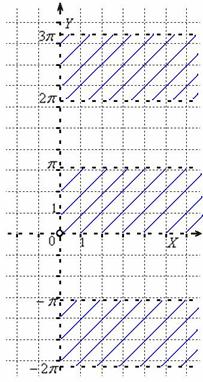мда …какой-то чертёж-призрак получился…  доброе приведение высшей математики…

Ответ: 

Следующий логарифм ваш:

Пример 11 Найти область определения функции 

В ходе решения придётся построить параболу, которая поделит плоскость на 2 части – «внутренность», находящуюся между ветвями, и внешнюю часть. Методика нахождения нужной части неоднократно фигурировала в статье Линейные неравенства и предыдущих примерах этого урока.

Решение, чертёж и ответ в конце урока.

Заключительные орешки параграфа посвящены «аркам»:

Пример 12 Найти область определения функции 

Решение: аргумент арксинуса должен находиться в следующих пределах:

Дальше есть две технические возможности: более подготовленные читатели по аналогии с последними примерами урока Область определения функции 1-ой переменной могут «ворочать» двойное неравенство и оставить в середине «игрек». Чайникам же рекомендую преобразовать «паровозик» в равносильную систему неравенств:

Система решается как обычно – строим прямые   и находим нужные полуплоскости. В результате: 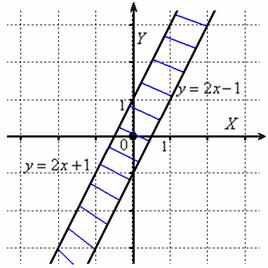Обратите внимание, что здесь границы входят в область определения и прямые проводятся сплошными линиями. За этим всегда нужно тщательно следить, чтобы не допустить грубой ошибки.

Ответ: область определения представляет собой решение системы 

Пример 13 Найти область определения функции 

В образце решения используется продвинутая техника – преобразуется двойное неравенство.

На практике также иногда встречаются задачи на нахождение области определения функции трёх переменных  . Областью определения функции 3-х переменных может являться всё трёхмерное пространство, либо его часть. В первом случае функция   определена для любой точки   пространства, во втором – только для тех точек  , которые принадлежат некоторому пространственному объекту, чаще всего –телу. Это может быть прямоугольный параллелепипед, эллипсоид, «внутренность»параболического цилиндра и т.д.  Задача отыскания области определения функции 3-х переменных обычно состоит в нахождении этого тела и выполнении трёхмерного чертежа. Однако такие примеры чрезвычайно редкИ (нашёл у себя всего пару штук), поэтому я ограничусь лишь обзорным абзацем и продолжу нарезать функцию 2-х переменных:

Линии уровня

Для лучшего понимания этого термина будем сравнивать ось   с высотой: чем больше значение «зет» – тем больше высота, чем меньше значение «зет» – тем высота меньше. Также высота может быть и отрицательной.

Функция   в своей области определения представляет собой пространственный график, для определённости и бОльшей наглядности будем считать, что это тривиальная поверхность. Что такое линии уровня? Образно говоря, линии уровня – это горизонтальные «срезы» поверхности на различных высотах. Данные «срезы» или правильнее сказать,сечения проводятся плоскостями  , после чего проецируются на плоскость  .

Определение: линией уровня функции   называется линия   на плоскости  , в каждой точке которой функция сохраняет постоянное значение:  .

Таким образом, линии уровня помогают выяснить, как выглядит та или иная поверхность – причём помогают без построения трёхмерного чертежа! Рассмотрим конкретную задачу:

Пример 14 Найти и построить несколько линий уровня графика функции

Решение: исследуем форму данной поверхности с помощью линий уровня. Для удобства развернём запись «задом наперёд»: 

Очевидно, что в данном случае «зет» (высота) заведомо не может принимать отрицательные значения (так как сумма квадратов неотрицательна). Таким образом, поверхность располагается в верхнем полупространстве (над плоскостью  ).

Поскольку в условии не сказано, на каких конкретно высотах нужно «срезать» линии уровня, то мы вольнЫ выбрать несколько значений «зет» на своё усмотрение.

Исследуем поверхность на нулевой высоте, для этого поставим значение   в равенство  :

Решением данного уравнения является точка  . То есть, при   линия уровня представляет собой точку.

Поднимаемся на единичную высоту и «рассекаем» нашу поверхность   плоскостью    (подставляем   в уравнение поверхности):

 

Таким образом, для высоты   линия уровня представляет собой окружность с центром в точке   единичного радиуса.

Напоминаю, что все «срезы» проецируются на плоскость  , и поэтому у точек я записываю две, а не три координаты!

Теперь берём, например, плоскость   и «разрезаем ей» исследуемую поверхность   (подставляем   в уравнение поверхности):

Таким образом, для высоты   линия уровня представляет собой окружность с центром в точке   радиуса  .

И, давайте построим ещё одну линию уровня, скажем, для  :

 – окружность с центром в точке   радиуса 3.

Линии уровня, как я уже акцентировал внимание, располагаются на плоскости  , но каждая линия подписывается – какой высоте она соответствует: 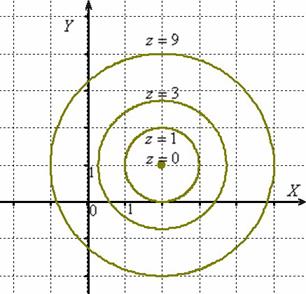Нетрудно понять, что другие линии уровня рассматриваемой поверхности тоже представляют собой окружности, при этом, чем выше мы поднимаемся вверх (увеличиваем значение «зет») – тем больше становится радиус. Таким образом, сама поверхность представляет собой бесконечную чашу с яйцевидным дном, вершина которой расположена на плоскости  . Эта «чаша» вместе с осью   «выходит прямо на вас» из экрана  монитора, то есть вы смотрите в её дно =)  И это неспроста! Только я так убойно наливаю на посошок =) =)

Ответ: линии уровня данной поверхности представляют собой концентрические окружности вида 

Примечание: при   получается вырожденная окружность нулевого радиуса (точка)

Само понятие линии уровня пришло из картографии. Перефразируя устоявшийся математический оборот, можно сказать, что линия уровня – это географическое место точек одинаковой высоты. Рассмотрим некую гору с линиями уровня 1000, 3000 и 5000 метров: 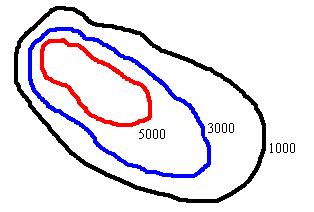На рисунке хорошо видно, что левый верхний склон горы гораздо круче правого нижнего склона. Таким образом, линии уровня позволяют отразить рельеф местности на «плоской» карте. Кстати, здесь приобретают вполне конкретный смысл и отрицательные значения высоты – ведь некоторые участки поверхности Земли располагаются ниже нулевой отметки уровня мирового океана.

Заключительное задание для самостоятельного решения:

Пример 15 Найти и построить линии уровня графика функции   при  . Охарактеризовать семейство   линий уровня и положение поверхности в пространстве.

Тут в отличие от предыдущей задачи даны конкретные значения «зет», для которых надо построить линии, и придумывать ничего не надо. Кажется слишком простым? Впечатление обманчиво – далеко не все читатели «гладко» оформят решение ;-)

Исследование формы поверхности с помощью линий уровня – метод эффективный, но довольно трудозатратный, поэтому крайне желательно знать, как выглядят распространённые на практике поверхности и быстро определять их по уравнению. На следующем уроке о пространственных поверхностях вы сможете не только почерпнуть много новой информации, но и научиться грамотно строить трёхмерные чертежи.

Желаю успехов!

Решения и ответы:

Пример 3: Решение: подкоренное выражение должно быть неотрицательным, кроме того, знаменатель не может обращаться в ноль, таким образом:  . Ответ: полуплоскость  , исключая саму прямую 

Пример 5: Решение: подкоренное выражение должно быть неотрицательным:  или, «разворачивая» неравенство:  Изобразим область определения на чертеже: 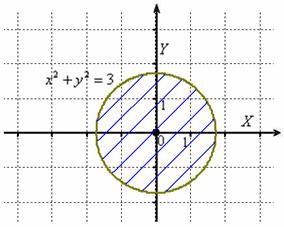Ответ:   – круг с центром в начале координат, радиуса  .

Пример 7: Решение: найдём область определения:  Выполним чертёж: 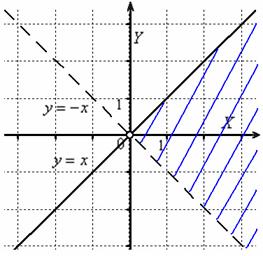Ответ: область определения представляет собой решение системы линейных неравенств 

Пример 9: Решение: найдём область определения: Неравенство   справедливо, когда   (1-ая координатная четверть) иликогда   (3-я координатная четверть). Условие   выполнено для всех точек плоскости, кроме начала координат. Изобразим область определения на чертеже: Ответ: 

Пример 11: Решение: найдём область определения: 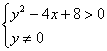Неравенству соответствует «внешняя» часть плоскости относительно параболы. Условие   исключает из области определения ось абсцисс. Выполним чертёж: 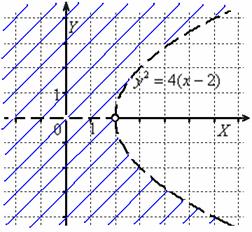Ответ: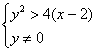 

Пример 13: Решение: аргумент арккосинуса находится в пределах: Вычтем «тройку» из каждой части: 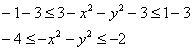Умножим каждую часть на –1. Так как умножение проводится на отрицательное число, значки «меньше либо равно» следует поменять на «больше либо равно»: «Развернём» неравенство в привычном направлении: Область определения представляет собой кольцо, ограниченное концентрическими окружностями  : 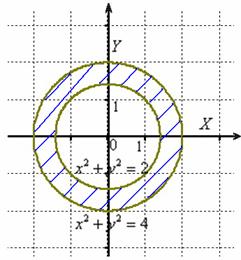Ответ: кольцо 

Пример 15: Решение: Перепишем функцию в виде   и найдём линии уровня для различных значений: 1) Если  , то   – гипербола, расположенная во 2-ой и 4-ой координатных четвертях. 2) Если  , то  . Полученное равенство справедливо в двух случаях: либо   и   – любое (это ось ординат), либо   и   – любое (это ось абсцисс). Таким образом, линия уровня   представляет собой две пересекающиеся прямые (координатные оси). 3) Если  , то   – гипербола, расположенная в 1-ой и 3-ей координатных четвертях. 4) Если  , то   – гипербола, расположенная в 1-ой и 3-ей координатных четвертях. Выполним чертёж: 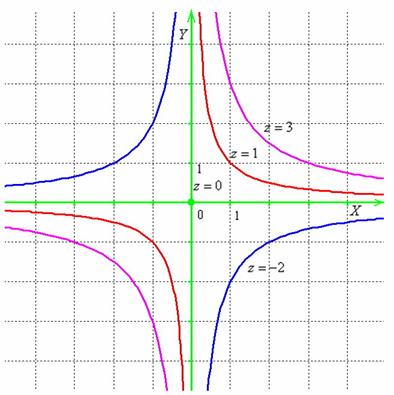Ответ: линии уровня функции имеют вид  , где  . Если  , то линии уровня представляют собой гиперболы, причём:  – в случае   они расположены 2-ой и 4-ой координатных четвертях, а сама поверхность   – ниже плоскости  ;  – в случае   гиперболы расположены 1-ой и 3-ей координатных четвертях, а сама поверхность   – выше плоскости  .  При   линия уровня распадается на две пересекающие прямые (координатные оси), то есть график функции   проходит через них. Примечание: исследуемая поверхность по форме весьма напоминает поверхность Примера 4.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)