Динамические структуры данных. Однонаправленный список
Не редко в структурах используют списки, потому что с ними удобнее работать, чем с массивами, когда не знаешь точное количество данных, когда в процессе работы приходится добавлять и удалять элементы.
Линейный список — это динамическая структура данных, каждый элемент которой посредством указателя связывается со следующим элементом. Из определения следует, что каждый элемент списка содержит поле данных (Data) (оно может иметь сложную структуру) и поле ссылки на следующий элемент (next). Поле ссылки последнего элемента должно содержать пустой указатель (NULL).
struct Data
{
int
a;
};
struct List
{
Data d;
List *next;
};
Каждый узел односвязного (однонаправленного связного) списка содержит указатель на следующий узел. Из одной точки можно попасть лишь в следующую точку, двигаясь тем самым в конец. Так получается своеобразный поток, текущий в одном направлении.
Динамические структуры данных. Стек и очередь
Стек - последовательный список переменной длины, включение и исключение элементов из которого производится только с одной стороны. Вершина стека — эта та его часть, через которую ведётся вся работа. На вершину стека добавляются новые элементы, и с вершины стека снимаются (удаляются) элементы.
В общем, стек — это односвязный список, для которого определены только две операции: добавление и удаление из начала списка. Примером стека может служить коробка, в которую сверху укладывают книги. Извлекать книги также приходится сверху.
struct Data
{
int a;
};
struct Stek
{
Data d;
Stek *next;
};
Функция добавления в стек (пример)
void Push(Stek **u, Data &x)
{
Stek *t = new Stek; // Память под новый элемент
t->d.a = x.a; // Заполнение полей
t->next = *u; // Подключаем новый элемент к имеющимся
*u = t; // Перенастройка вершины
}
Очередь - это линейная динамическая структура данных, для которой выполняется правило: добавление новых данных возможно только в конец этой структуры, а удаление (извлечение) — только с начала. Очередь может быть определена как частный случай односвязного списка, который обслуживает элементы в порядке их поступления. Как и в «живой» очереди, здесь первым будет обслужен тот, кто пришел первым. Очередь — это линейный список, для которого определены всего две основные операции: добавление в конец и извлечение с начала. Значит, удобно иметь два указателя: на начало и конец этой динамической структуры.
Выделяют два способа программной реализации очереди. Первый из них основан на базе массива, а второй на базе указателей (связного списка). Первый способ – статический, т. к. очередь представляется в виде простого статического массива, второй – динамический.
Динамические структуры данных. Бинарное дерево.
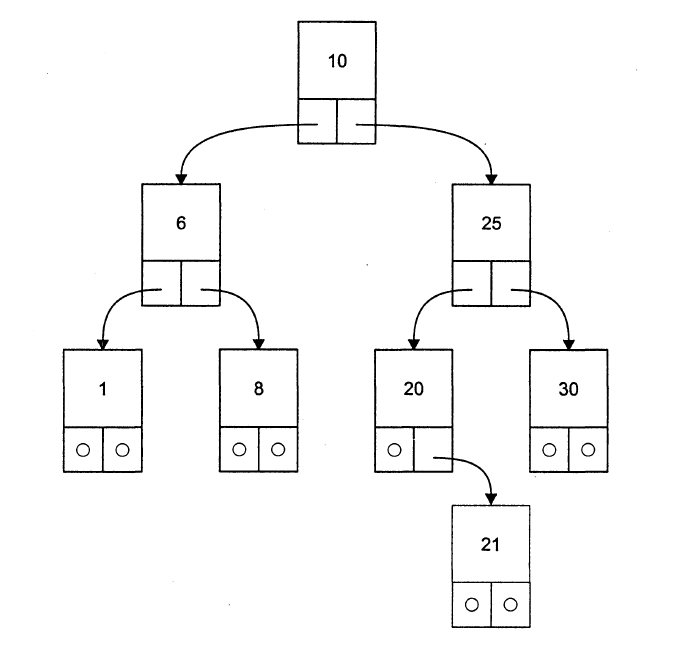Бинарное
дерево — это
динамическая структура данных, состоящая
из узлов, каждый из которых содержит,
кроме данных, не более двух ссылок на
различные бинарные деревья. На каждый
узел имеется ровно одна ссылка. Начальный
узел называется корнем
дерева. На
рисунке приведен пример бинарного
дерева. Узел, не имеющий поддеревьев,
называется листом.
Исходящие узлы называются предками,
входящие — потомками.
Высота дерева определяется количеством уровней, на которых располагаются его узлы. Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого под-дерева —больше, оно называется деревом поиска. Одинаковые ключи не допускаются. В дереве поиска можно найти элемент по ключу, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения ключа в каждом узле. Такой поиск гораздо эффективнее поиска по списку, поскольку время поиска определяется высотой дерева, а она пропорциональна двоичному логарифму количества узлов.
Основные функции для работы с бинарным деревом: добавление нового узла(add), поиск элемента (serch), обход (view), очистить (clean).
Удаление узла из дерева представляет собой не такую простую задачу, по-скольку удаляемый узел может быть корневым, содержать две, одну или ни одной ссылки на поддеревья. Для узлов, содержащих меньше двух ссылок, удаление тривиально. Чтобы сохранить упорядоченность дерева при удалении узла с двумя ссылками, его заменяют на узел с самым близким к нему ключом. Это может быть самый левый узел его правого поддерева или самый правый узел левого под-дерева (например, чтобы удалить из дерева на рисунке узел с ключом 25, его нужно заменить на 21 или 30, узел 10 заменяется на 20 или 8, и т. д.).