7. Определенный интеграл, его геометрический смысл и свойства

Вычисление площади фигуры является одной из наиболее не простых проблем теории площадей. В школьном курсе геометрии мы научились находить площади основных геометрических фигур, например, круга, треугольника, ромба и т.п. Однако намного чаще приходится сталкиваться с вычислением площадей более сложных фигур. При решении подобных задач приходится прибегать к интегральному исчислению.

В этой статье мы рассмотрим задачу о вычислении площади криволинейной трапеции, причем подойдем к ней в геометрическом смысле. Это позволит нам выяснить прямую связь между определенным интегралом и площадью криволинейной трапеции.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (то есть, неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = a и x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).

Подойдем к задаче вычисления площади криволинейной трапеции следующим образом. В разделе квадрируемые фигуры мы выяснили, что криволинейная трапеция является квадрируемой фигурой. Если разбить отрезок [a; b] на n частей точками и обозначить , а точки выбирать так, чтобы при , то фигуры, соответствующие нижней и верхней суммам Дарбу, можно считать входящей P и объемлющей Q многоугольными фигурами для G.

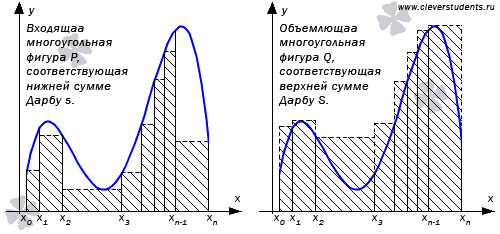
Таким образом, и при увеличении количества точек разбиения n, мы придем к неравенству , где - сколь угодно малое положительное число, а s и S – нижняя и верхняя суммы Дарбу для данного разбиения отрезка [a; b]. В другой записи . Следовательно, обратившись к понятию определенного интеграла Дарбу, получаем .

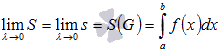Последнее равенство означает, что определенный интеграл 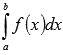для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.

То есть, вычислив определенный интеграл , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.

Замечание.

Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как .

8. Формула Ньютона-Лейбница. Интегрирование по частям и замена

переменной в определенном интеграле

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

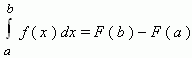
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

9. Несобственные интегралы, их сходимость, признаки сравнения

Рассмотрим обобщения понятия интеграла – интегралы с бесконечными пределами и интегралы от неограниченных функций. Это, по существу, новые понятия, поскольку при определении интеграла предполагалось, что отрезок интегрирования конечен, а подынтегральная функция определена и ограничена на этом отрезке. В новой же конструкции придется рассматривать пределы не только интегральных сумм, но и пределы определенных интегралов.

Пусть функция  определена для всех , где - некоторое число, и интегрируема на любом отрезке , где . Если существует конечный предел

,

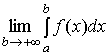то говорят, что функция   интегрируема в несобственном смысле на промежутке . Этот предел называется несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода и обозначается

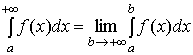
Обычно, если конечный предел существует, то говорят, что несобственный интеграл сходится. Если же конечного предела не существует, то говорят, что несобственный интеграл расходится.

Если с>a, то несобственные интегралы

  и  сходиться или расходиться одновременно.

Действительно, если для любого b>a функция  интегрируема, то

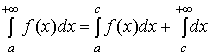, откуда и следует что оба несобственных интеграла одновременно или существуют, или не существуют.

Аналогично можно определить несобственные интегралы и для других бесконечных промежутков.

Если функция определена при  и интегрируема на любом отрезке , где ,

то

Если же для функции  существуют несобственные интегралы 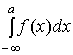 и , то существует и несобственный интеграл 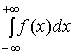, определенный формулой

,

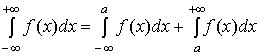причем существование и значение несобственного интеграла  не зависят от выбора точки .

Чтобы лучше осознать идею, лежащую в основе понятия несобственного интеграла, рассмотрим положительную убывающую на промежутке  функцию

Интеграл 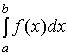 численно равен площади фигуры, изображенной на рисунке 10.1. При возрастании  эта площадь увеличивается и, если , то площадь может или возрастать безгранично, или оставаться ограниченной, то есть стремиться к некоторому пределу, который представляет собой площадь, заключенную между осью ОХ и кривой вправо от точки .

Пример. Вычислить несобственный интеграл

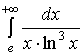
Решение. По определению

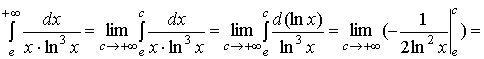
Несобственный интеграл сходится.

Иногда, при вычислении несобственного интеграла, для краткости опускается предельный переход, например,

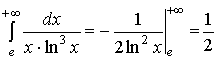
На несобственные интегралы переносятся многие свойства интеграла Римана. Сформулируем эти свойства для интегралов вида . Для других видов интегралов на бесконечных промежутках эти свойства также справедливы.

1)     Если интеграл  сходиться, С – некоторое число, то интеграл  также сходиться и

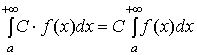
2)     Если интегралы  и  сходятся, то интеграл 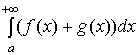 только сходится и

 

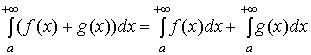
3)     Если функции  и  интегрируемы при , то

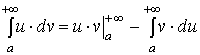
4)     Пусть функция  непрерывна при , функция  определена, непрерывна и имеет непрерывную производную на промежутке  конечном или бесконечном, где <

Тогда

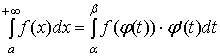
Формула называется формулой замены переменной в несобственном интеграле.

Доказательства перечисленных утверждений следуют из свойства определенных интегралов и пределов функций.

Часто бывает достаточно только установить, сходится интеграл или расходится, не вычисляя его значения, Для этого используются следующие признаки сходимости

Критерий Коши. Если функция  интегрируема на отрезке > , то для сходимости несобственного интеграла  необходимо и достаточно, чтобы для любого сколь угодно малого положительного числа >0 существовало число  такое, что для любых двух чисел > и > , выполнялось неравенство

<

Признак сравнения. Пусть функции и  определены и неотрицательны при , интегрируемы на любом отрезке < и

 при ,

тогда, если интеграл сходится, то сходится и интеграл . А если интеграл  расходится, то расходится и интеграл

Признак сравнения чаще формулируется в виде следствий.

Следствие 1. Если при

  ,

интеграл  сходится, то сходится и интеграл , а если интеграл    расходится, то расходится и интеграл

Следствие 2. Если при

  >0 и , где 0<k< ,

то интегралы   и  сходятся или расходятся одновременно.

Интеграл  называется абсолютно сходящимся, если сходится интеграл 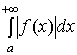. Несобственный интеграл  называется условно сходящимся, если он сходится, а  расходится. Из сходимости интеграла следует сходимость интеграла .

Методы исследования сходимости несобственных интегралов, при которых исследование сходимости данного интеграла сводится и исследованию сходимости другого интеграла, который сходится лучше исходного, называется методами улучшения сходимости.

Признак сходимости Дирихле.

Пусть функция  непрерывна и имеет ограниченную первообразную при , функция  непрерывна дифференцируема при  и монотонно убывает, причем , тогда интеграл

 с

сходится.

Доказательство. По условию, функция  непрерывна, а следовательно и интегрируема на любом отрезке < < .  – первообразная функции .

Рассмотрим интеграл 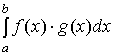 и проинтегрируем его по частям:

Так как функция  ограничена при , то <M, где M>0 – некоторое число, тогда , поэтому

 

Поскольку функция  монотонно убывает, то производная  при , тогда

,

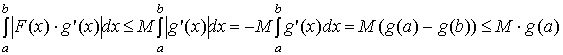поскольку