1.3.2. Векторные характеристики поля излучения

Рассмотрим распространение излучения около точки А пространства, определяемой радиус–вектором г, в пределах телесного угла dΩ в направлении единичного вектора Ω, который задан плоскими углами θ и φ (рис. 2).

Пусть F₁; (г, Е, θ, φ) есть число частиц излучения вида i, обладающих энергией в пределах от Е до Е + dЕ и пересекающих единичную площадку, перпендикулярно расположенную к направлению единичного вектора Ω. Функция F₁ (г, Е, θ, φ) выражает дифференциальное энергетическое и угловое распределение флюенса частиц около точки А пространства. Проинтегрировав эту функцию по углам, получим энергетическое распределение флюенса частиц:

Зная соотношение между флюенсом и плотностью потока частиц, можем записать энергетическое распределение плотности потока

где t — время.

Формулы (6) и (7) характеризуют распределение частиц по энергии в данном излучении. Функции Е (г, Е, t) и φ_N (г, Е) представляют собой энергетический спектр излучения. Если эти функции определены не только для фиксированной точки А при определенном значении радиус-вектора г, но и для различных точек пространства, так что г выступает в качестве независимой переменной, то они выражают пространственно-энергетическое распределение излучения. Первоначально введенная функция F_i (г, Е, θ, φ) в этом случае характеризует пространственное (г), энергетическое (Е) и угловое (θ, φ)) распределения излучения.

1.4. Связь между характеристиками поля излучения и показаниями детектора

Исчерпывающая информация о поле частиц будет в том случае, если известно, как распределены частицы во времени, пространстве и по энергиям. Поле частиц характеризуют функцией Ф(r,Е,Ω,t)dEdΩdt, которую называют дифференциальным (по энергии, времени и углам) потоком.

Дифференциальный поток – это число частиц с энергией Е в интервале dE, движущихся в направлении Ω, в интервале телесного угла dΩ и пересекающих в точке r в момент времени t в интервале dt единичную площадку, нормаль к которой совпадает с направлением Ω.

Интегральный поток Ф(r,t)dt – это интеграл от дифференциального потока по всем энергиям и направлениям движения частиц.

Таким образом, интегральный поток – это число частиц в момент времени t в интервале dt, пересекающих по всем направлениям сферу с единичной площадью центрального сечения и с центром в точке r.

Введем еще понятие дифференциального тока

J(r,Е,Ω,t)dEdΩdt.

Дифференциальный ток – это число частиц с энергией Е в интервале dE, пересекающих в данный момент времени t в интервале dt, в направлении Ω, в интервале телесного угла dΩ единичную площадку, нормаль к которой задана вектором ΩJ.

Аналогично интегральному потоку определяется интегральный ток, который является векторной величиной и дает разность между числом частиц, прошедших за время dt в момент t через единичную площадку, перпендикулярную вектору ΩJ со стороны полупространства, куда направлен вектор ΩJ, и числом частиц, прошедших через ту же площадку, но со стороны другой половины пространства. Интегральный ток при изотропном дифференциальном потоке равен нулю.

Связь между током и потоком легко установить. Пусть в точке r = 0 угловое распределение потока задано в сферической системе координат, начало которой также в точке r = 0. Надо найти дифференциальный ток через площадку, нормаль к которой задана углом Θ0 = 0. Тогда очевидно, что связь между дифференциальным током и потоком будет иметь следующий вид:

J(r,Е,Ω,t)= Ф(r,Е,Ω,t)cosΘ.

В общем случае, когда нормаль к площадке задана углами Θ0 и φ0, связь между дифференциальными током и потоком:

J(r,Е,Ω,t)= Ф(r,Е,Ω,t)[ cosΘcos Θ0 + sinΘsin Θ0cos(φ0- φ)].

Рассмотрим несколько детекторов с конкретными свойствами и установим, какую характеристику поля они измеряют. Для простоты будем считать, что характеристики поля постоянны во времени, энергии частиц имеют одно, определенное значение, а детектор не возмущает поля частиц в точке, где он находится.

Если размеры детектора таковы, что Σ·l « 1 (Σ–макроскопическое сечение взаимодействия нейтронов или γ-квантов с веще­ством детектора; l – размер детектора), то такой детектор будет измерять величину, пропорциональную интегралу от функции Ф(Ω, r), т.е. величину, пропорциональную потоку:

Ф0(r)=const .

Детектор в виде пластины такой толщины, что Σ·l >1 измеряет величину, пропорциональную сумме составляющих интегрального тока:

При регистрации заряженных частиц, эффективность регистрации которых считается равной единице и независимой от направления падения на детектор, детектор в виде тонкой пластины измерит величину, пропорциональную сумме составляющих интегрального тока. Если же детектор – сферический, то его показания будут пропорциональны интегральному потоку. Если регистрируется излучение с непрерывным распределением по энергии, то показания детектора при Σ·l«1 пропорциональны числу реакций, т.е.

Когда Σ(E) ≈ E- ½ (n,p- и n,α – реакции на легких ядрах), то показания детектора пропорциональны плотности нейтронов (число нейтронов в единице объема).

Для измерения дифференциальных характеристик поля эффективность детектора должна быть большой только для излучения, движущегося в определенном направлении. Это достигается с помощью коллиматоров. Если детектор поместить внутри непрозрачной для частиц сферы, в которой вырезать конус с углом ΔΩ, то детектор будет регистрировать частицы в направлении Ω в телесном угле ΔΩ. Проведя измерения при всех значениях Ω, получаем величины εd в точке, где расположен детектор и которая является центром вращения конуса ΔΩ. В зависимости от выбора системы координат, можно найти J(r,Ω) по измеренным εdФ(r,Ω).

Таким образом, для измерения угловых характеристик ноля необходимо хорошее угловое разрешение детектора (узкая направленность). Если считать, что стенки коллиматоров являются абсолютно черными для частиц, то угловое разрешение детектора с цилиндрическим коллиматором

Θ*=arctg(2r0/l),

где r0 и l – радиус и длина коллиматора.

Поскольку стенки коллиматоров не являются абсолютно непрозрачными, то необходимо учитывать ухудшение углового разрешения детектора за счет прозрачности стенок коллиматора. Реальная величина ΔΩ будет больше оптической ΔΩo, и при достаточно малых величинах ΔΩo с хорошей точностью можно считать, что

ΔΩ/ΔΩo=1+2/Σ·l,

где Σ – полное сечение взаимодействия излучения со стенками коллиматора.

Рассмотрим несколько примеров.

Пример 1. Определить плотность потока частиц в некоторой точке пространства , для которой угловое распределение поля излучения изотропно и в единичный телесный угол движется φ0( ) частиц/(см2 ·с·ср).

Плотность потока частиц рассчитаем по формуле:

част/(м2·с),

принимая φ , где θ и ψ соответственно полярный и азимутальный углы в сферической системе координат.

Тогда:

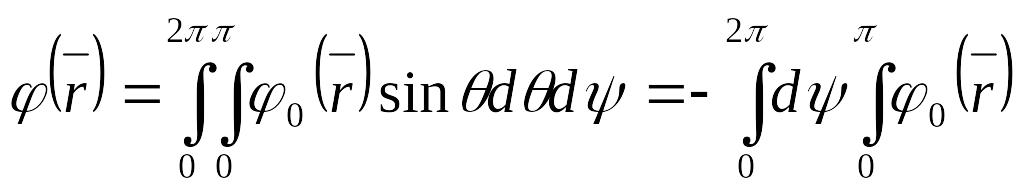и .

В соответствии с формулой:

.

Таким образом, для изотропного распределения излучения плотность тока обращается в нуль, а плотность потока естественно не равна нулю.

Физически обращение плотности тока в нуль для рассматриваемой задачи можно понять, если учесть, что каждая частица, пролетающая слева направо, компенсируется при подсчете плотности тока частицей пролетающей справа налево.

Пример 2. Определить плотность потока и плотность тока частиц через помещенную в точке единичную площадку, если плотность тока проходящую через нее излучения имеет косинусоидальное распределение относительно нормали к площадке и в единичный телесный угол в единицу времени движется J0cos(θ/π) частиц при 0≤θ≤π/2; при π/2<θ<π излучение отсутствует.

Плотность потока частиц в соответствии с формулой

част/(м2·с)

и с учетом формулы:

будет равна:

.

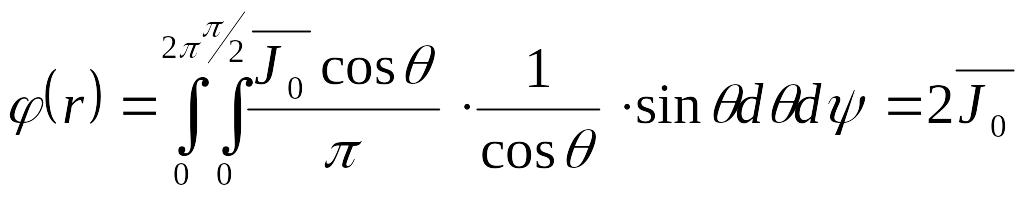Вектор тока совпадает с осью симметрии, модуль вектора плотности тока можно рассчитать по формуле:

с учетом соотношения

т.е.

.

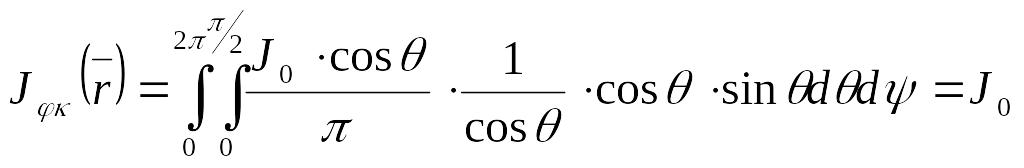Таким образом, плотность тока в этой задаче в два раза меньше плотности потока:

.