1. Рамка с током в однородном магнитном поле.

а) Прямоугольная рамка

Поместим прямоугольную рамку с током I в однородное магнитное поле с индукцией B, так чтобы его силовые линии были параллельны площади рамки.

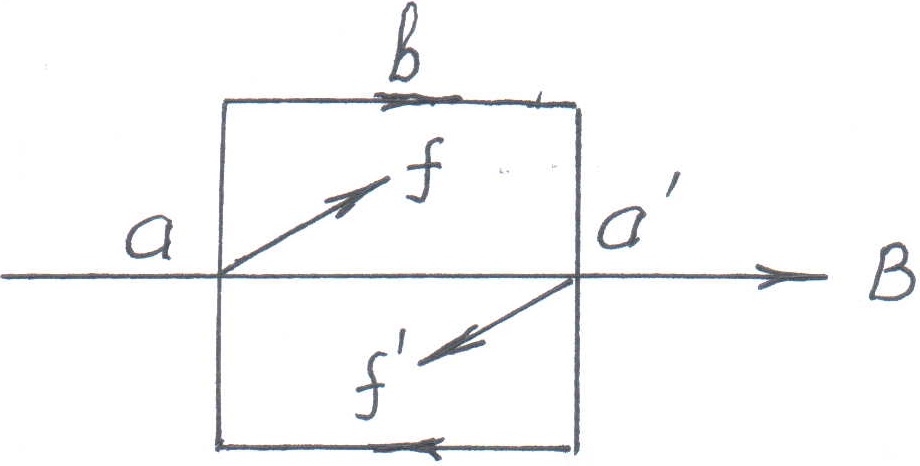
Рис.12.

По закону Ампера на каждый элемент рамки должна будет действовать сила, равная:

.

Для всех элементов, находящихся на сторонах и , эта сила равна нулю, так как угол между и равен нулю или .

На стороны и действует результирующая сила , так как угол между

и равен либо , либо .

Следовательно, на сторону действует сила, направленная от нас за чертёж, а на сторону

- от чертежа к нам.

Эта пара сил будет создавать вращательный момент равный , где кратчайшее расстояние между линиями действия сил и .

Тогда

Учитывая, что магнитный момент рамки направлен по нормали к поверхности рамки, т.е. в начальный момент , можно записать

б) рамка произвольной формы.

Пусть теперь в однородном магнитном поле находится контур произвольно расположенный относительно силовых линий поля.

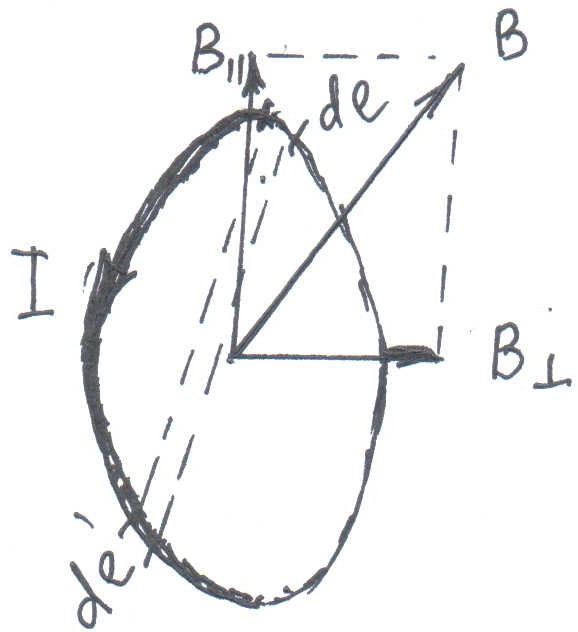
Рис.13.

На каждый элемент будет действовать сила . Поскольку направлен относительно поверхности контура под некоторым углом , разложим его на

составляющие, одна из которых параллельна плоскости контура, другая перпендикулярна ей. Составляющая создаст силу, стремящуюся сжать или растянуть контур в зависимости от направления тока в контуре. Составляющая обеспечивает появление пары сил, действующих на элементы контура и , которые и создадут вращательный момент.

в) потенциальная энергия контура в магнитном поле

Определим работу, которую необходимо совершить, чтобы повернуть контур в магнитном поле на угол .

Считая, что С=0, так как работа при нулевом угле поворота равна нулю, получим

Эта работа идёт на увеличение потенциальной энергии в магнитном поле

.

2. Контур с током в неоднородном магнитном поле.

Пусть контур с током I, находится в неоднородном магнитном поле с индукцией , которая меняется вдоль оси ОХ. Для простоты будем считать, что вдоль других осей координат изменением индукции можно пренебречь

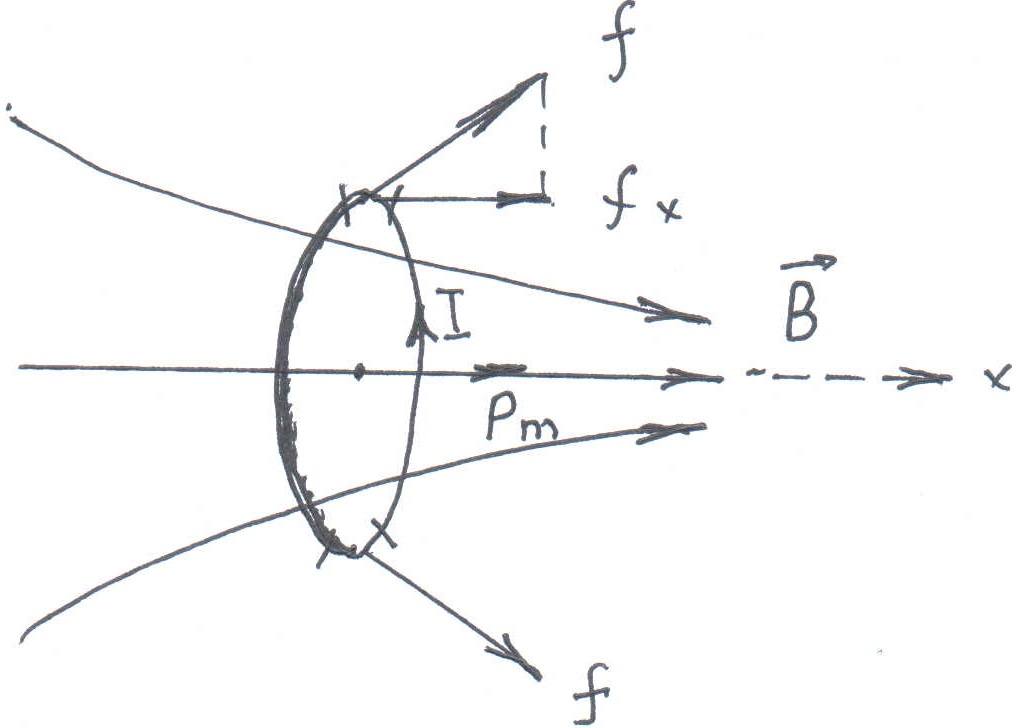
Рис14.

Тогда на каждый элемент будет действовать сила . Эти силы будут образовывать конический веер. Каждую из этих сил можно разложить составляющие, одна из которых будет направлена так, что при её воздействии ( при направлении тока указанном на рис.) контур будет втягиваться в область более сильного поля. Если изменить направление тока, то силы будут выталкивать контур из магнитного поля.

В механике было получено, что , где W – потенциальная энергия системы.

В нашем случае эта энергия равна , следовательно

Если индукция магнитного поля меняется по всем направлениям, то

Проводник с током длиной , представляющий собой участок замкнутой цепи, может свободно перемещаться при помощи скользящих контактов во внешнем однородном магнитном поле. Вектор индукции магнитного поля направлен от нас за чертёж

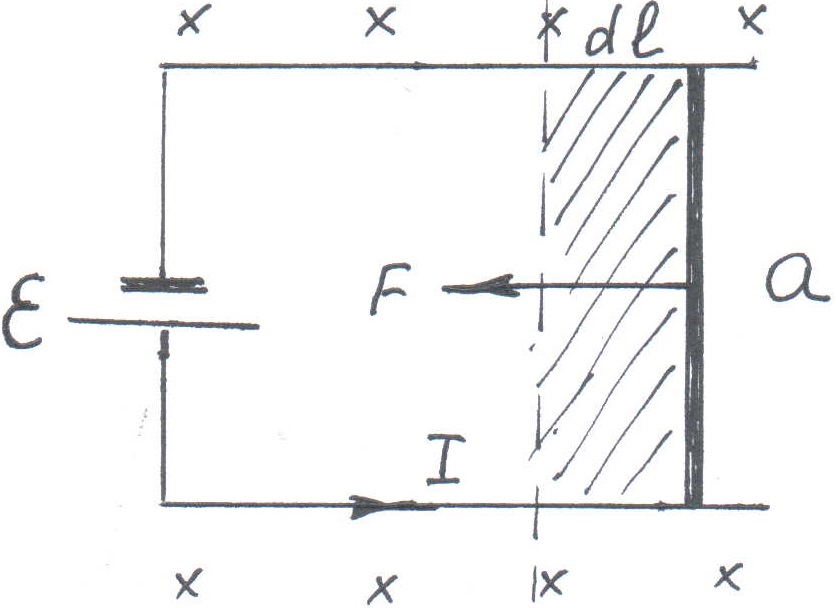
Рис.15.

По проводнику течёт ток I. При направлении тока указанном на Рис. На проводник будет действовать сила, направленная влево и численно равная согласно закону Ампера

.

При перемещении проводника на отрезок будет совершена работа равная:

, где .

Назовём потоком вектора магнитной индукции физическую величину, численно равную:

Ф ,

где проекция вектора на направление положительной нормали к поверхности рассматриваемого контура.

В случае, если и , то dФ , и элементарная работа будет равна

Полученный результат справедлив и для неоднородного поля, ориентированного произвольно к поверхности, в которой лежит проводник.

Для того, чтобы доказать это, надо разбить проводник на элементарные отрезки da и просуммировать все элементарные работы, совершаемые в магнитном поле над каждым элементом da :

,

где и .

Эту работу совершает не сила Лоренца, работа которой всегда равна нулю, а силы источника, поддерживающие ток в проводнике.

ЛЕКЦИЯ 7.

МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ.

1. Намагничивание магнетиков. Вектор намагниченности.

2. Теорема Гаусса для вектора магнитной индукции

3. Напряженность магнитного поля. Теорема о циркуляции вектора Н.

4. Магнитомеханические явления.

5. Виды магнетиков

До сих пор мы рассматривали взаимодействие проводника с током и магнитного поля в вакууме. Однако, все вещества по-разному реагируют на внешнее магнитное поле.

Другими словами, среда должна оказывать свое дополнительное влияние на это взаимодействие.

Любое вещество в магнитном поле приобретает новые свойства – намагничивается.

Намагниченное вещество создаёт своё собственное магнитное поле , которое накладывается на внешнее .

Для объяснения процесса намагничивания вещества Ампер предложил следующую гипотезу.

Он считал, что в молекулах вещества циркулируют круговые токи. Каждый такой ток обладает магнитным моментом и создает в окружающем его пространстве магнитное поле. В отсутствии внешнего магнитного поля магнитные моменты молекулярных токов ориентированы произвольным образом, вследствие чего, результирующее поле молекулярных токов равно нулю и суммарный магнитный момент всего вещества тоже равен нулю.

Под действием внешнего поля магнитные моменты молекулярных токов приобретают преимущественную ориентацию, и у вещества появляется результирующий магнитный момент – вещество намагничивается.

Процесс намагничивания характеризуется физической величиной, которая называется вектором намагничивания или намагниченностью.