Вопросы для защиты задачи

1. Какое движение твердого тела называется поступательным и какими свойствами оно обладает?

2. Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно задается?

3.Дайте определения угловой скорости и углового ускорения.

4.Как определить вращательную скорость точки при вращении тела?

5.Как определяются вращательное и центростремительное ускорения при вращении тела?

Задача 4. Определение кинематических характеристик плоского движения

Кривошип OA длиной 0,2 м вращается рав­номерно с угловой скоростью ω_OA = 10 с^–1 и при­водит в движение шатун АВ длиной 1 м. Пол­зун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с вертикалью угол 45° (рисунок 16.1).

Решение.

1. Определение скоростей. Вычис­лим скорость точки А как точки вра­щающегося кривошипа:

.

Она направлена перпендикулярно ОА (рисунок 17.1).

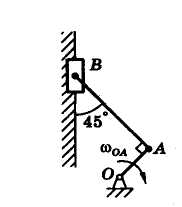
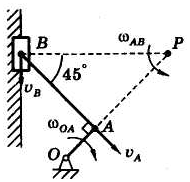
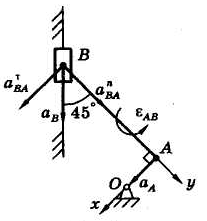
Рисунок 16.1 Рисунок 17.1 Рисунок 18.1

Скорость v_B ползуна направлена по направляющей вертикально.

Для шатуна АВ, совершающего плоское движение, теперь известны направления скоростей двух его то­чек: А и В. Восставляя перпендику­ляры к векторам этих скоростей, на­ходим точку Р их пересечения — МЦС шатуна.

Используя известную формулу для скоростей точек при плоском движении, получаем ; .

Из треугольника АВР имеем |АР| = 1 м; |ВР| = м, и тогда

.

2. Определение ускорений. Вычислим сначала ускоре­ние точки А как точки кривошипа: .

Здесь вращательное ускорение , так как , поскольку .

Тогда полное ускорение точки А равно центростремительному

и направлено к оси вращения — точке О (рисунок 18.1).

Для вычисления ускорения точки В воспользуемся тео­ремой о сложении ускорений, взяв точку А в качестве полюса:

. (1)

Центростремительное ускорение точки В в относи­тельном вращении вокруг точки А по модулю равно , и направлено от точки В к полю­су — точке А.

Модуль вращательного ускорения определяется по формуле и пока не может быть вычислен, поскольку неизвестна величина углового ускорения . Направление вектора также не может быть определе­но однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедлен­ным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление совпадет с направле­нием , а вектор направим перпендикулярно от­резку ВА по ходу углового ускорения.

Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать дви­жение ползуна ускоренным и направим ускорение в ту же сторону, что и скорость (рисунок 17.1, 18.1).

Теперь в равенстве (1) все ускорения имеют определен­ное направление, и мы можем записать это уравнение в проекциях на выбранные оси:

.

Из последнего уравнения получаем , тогда из первого уравнения

.

Отсюда следует, что

.

Отрицательные знаки у величин и показывают, что их истинные направления противоположны принятым.

№ вар.	ОА	АВ	α	ωOA
1	0,5	1,1	45	10
2	0,4	1,2	45	11
3	0,3	1,3	45	12
4	0,2	1,4	45	13
5	0,95	1,5	45	14
6	0,85	1,6	45	15
7	0,75	1,7	45	16
8	0,65	1,8	45	17
9	0,55	1,9	45	18
10	0,45	2	45	19
11	0,35	1,1	45	20
12	0,25	1,2	45	21
13	0,9	1,3	45	22
14	0,8	1,4	45	23
15	0,7	1,5	45	24
16	0,6	1,6	45	25
17	0,5	1,7	45	26
18	0,4	1,8	45	27
19	0,3	1,9	45	28
20	0,2	1,9	45	29