Граничные условия

Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме. Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе:

СИ	Словесное выражение
	непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля
	тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе

где   — единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,   — плотность поверхностных свободных токов вдоль границы. Аналогичным образом, выбирая область интегрирования в первой паре интегральных уравнений в виде цилиндра бесконечно малой высоты, пересекающего границу раздела так, что его образующие перпендикулярны границе раздела, можно получить:

СИ	Словесное выражение
	Показывают непрерывность нормальной компоненты вектора магнитной индукции

где   — поверхностная плотность свободных зарядов

Из уравнения непрерывности можно получить граничное условие для токов:

Частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. В результате тангенциальная компонента электрического и нормальная магнитного поля на границе с идеальным проводником равны нулю:

Билет 18.

Энергия взаимодействия зарядов. Потенциальная энергия электростатического взаимодействия двух точечных зарядов  и , находящихся на расстоянии друг от друга, рассчитывается по формуле:

Придадим этой формуле несколько иной вид: 

здесь  потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать  где  потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь перепишем выражение (1) в симметричной форме, легко допускающей обобщение.

В этой формуле два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но энергия взаимодействия не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды - из-за этого и появляется в формуле множитель 1/2.  Если система состоит из нескольких зарядов , , … , …  ( = 1, 2, … ), то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов можно заменить на суммирование по самим зарядам, то есть записать: .  - потенциал поля в точке, где находится заряд , причем поля, создаваемого всеми зарядами, кроме самого заряда .  Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим пример расчета энергии электростатического взаимодействия.  Пусть три одинаковых точечных заряда, величины которых равны между собой  =  =  = , расположены в вершинах правильного треугольника со стороной . Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен: В соответствии с формулой (3) энергия взаимодействия зарядов равна:  . Такую работу совершит электрическое поле при удалении всех зарядов на бесконечное расстояние друг от друга.  Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной _, то их энергия окажется равной:  При таком смещении работа электрического поля будет равна уменьшению энергии системы:  Обратите внимание, при эта работа становится в точности равной начальной энергии .  Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся,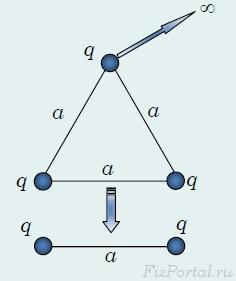 то энергия системы станет равной  при этом поле совершит работу 

Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу . В итоге начальная энергия полностью расходуется на совершение полной работы .