
- •Содержание
- •1. Распространение радиоволн в идеальном однородном диэлектрике
- •2.Распространение плоских радиоволн в однородной проводящей среде
- •3. Принцип Гюйгенса и зоны Френеля
- •4. Отражение радиоволн от поверхности плоской Земли
- •5. Отражение плоских радиоволн на границе раздела двух сред
- •5.1. Коэффициент отражения вертикально поляризованной волны
- •5.2. Коэффициент отражения горизонтально поляризованной волны
- •6. Влияние шероховатости отражающей поверхности
- •7. Распространение радиоволн при наличии экранирующих препятствий
- •7.1. Эффект "усиления препятствием"
- •8. Распространение радиоволн при антеннах, поднятых над плоской Землей
- •8.1. Горизонтальная поляризация падающей волны
- •8.2. Вертикальная поляризация падающей волны
- •Тогда получаем, что
- •Анализ формулы Введенского показывает, что
- •9. Поверхностное распространение радиоволн
- •10. Напряжённость поля радиоволны, распространяющейся вдоль земной поверхности
- •10.1. "Взлетная" и "посадочная" площадки
- •10.2. Распространение радиоволн вдоль неоднородной трассы
- •10.3. Береговая рефракция
- •11. Влияние сферичности отражающей поверхности
- •12. Распространение радиоволн в тропосфере
- •Коэффициент преломления n в тропосфере обычно определяется с помощью полуэмпирической формулы
- •12.1. Атмосферная рефракция Пусть радиоволна распространяется в плоскослоистой атмосфере (рис. 12.1). Согласно закону преломления
- •12.2. «Эквивалентный» радиус Земли
- •12.3. Виды атмосферной рефракции
- •12.4. Флуктуации радиосигнала и многолучевость распространения
- •12.5. Рассеяние укв на турбулентных неоднородностях
- •12.6. Полоса пропускания тропосферного канала
- •12.7. Поглощение радиоволн в тропосфере
- •13. Распространение радиоволн в ионосфере
- •13.1 Образование и строение ионосферы
- •13.2. Преломление радиоволн в ионосфере
- •13.3. Влияние магнитного поля на распространение радиоволн в ионосфере
- •13.4. Эффект Фарадея
- •13.5. Распространение радиоволн в простом ионосферном слое
- •13.6. Теоремы эквивалентности
- •13.7. Вертикальное зондирование ионосферы
- •13.8. Поглощение в ионосфере
- •Литература
2.Распространение плоских радиоволн в однородной проводящей среде
В земных условиях к таким средам обычно относят ионосферу, водную толщу, почву. Здесь проводимость 0, поэтому система уравнений Максвелла приобретает вид
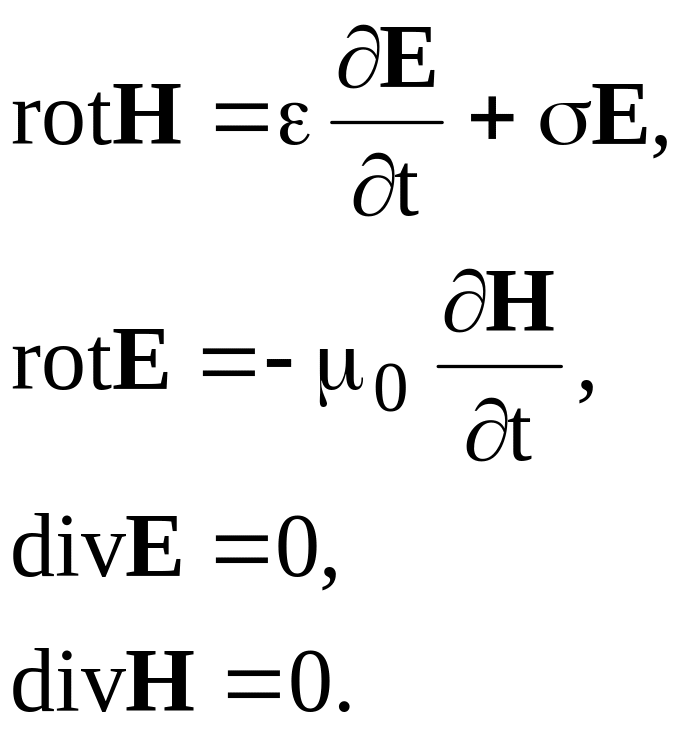 (2.1)
(2.1)
Полагая,
что поле создается гармоническим током
антенны, т. е. E
eit,
имеем
![]() ,
откуда
,
откуда
![]() .
Подставив это выражение в первое
уравнение системы (2.1), получаем:
.
Подставив это выражение в первое
уравнение системы (2.1), получаем:
![]() (2.2)
(2.2)
![]() называется
комплексной диэлектрической проницаемостью.
называется
комплексной диэлектрической проницаемостью.
Уравнение
(2.2) отличается от аналогичного из (1.2)
лишь тем, что
заменяется на к.
Все остальные уравнения систем (2.1) и
(1.2) совпадают, поэтому правомерно
использовать результаты, полученные
для идеального диэлектрика, заменив в
них '
на относительную комплексную
диэлектрическую проницаемость
![]()
![]() .
.
Представим
![]() в виде
в виде
![]() .
Тогда из (1.7) следует
.
Тогда из (1.7) следует
![]() ,
(2.3)
,
(2.3)
или в тригонометрической форме
![]() .
(2.4)
.
(2.4)
Из
(2.4) следует, что в проводящей среде волна
распространяется со скоростью
![]() ,
а амплитуда напряженности её поля с
расстоянием уменьшается, т. е. имеет
место затухание волны.
,
а амплитуда напряженности её поля с
расстоянием уменьшается, т. е. имеет
место затухание волны.
Напряжённость магнитного поля радиоволны в проводящей среде
 .
(2.5)
.
(2.5)
Используя
в (2.5) представление
![]() ,
получаем
,
получаем
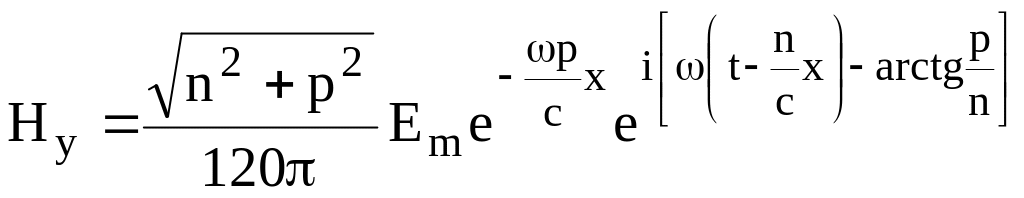 ,
(2.6)
,
(2.6)
соответственно, в тригонометрической форме
![]() .
(2.7)
.
(2.7)
Таким образом, при распространении в проводящей среде:
1) волна остается поперечной;
2)
по мере распространения волны в
направлении x
её амплитуда уменьшается по закону e
-x,
где
![]()
коэффициент поглощения средой;
коэффициент поглощения средой;
3)
электрическая и магнитная составляющие
поля радиоволны распространяются с
одинаковой скоростью
![]() ;
;
4)
в каждой точке пространства магнитное
поле сдвинуто по фазе по отношению к
электрическому полю на угол
![]() ;
;
5)
амплитуда магнитного поля связана с
амплитудой электрического поля
соотношением
![]() .
.
Рассматривая
представления
![]() и
и
![]() как
систему двух уравнений, нетрудно
получить, что
как
систему двух уравнений, нетрудно
получить, что
 ,
,
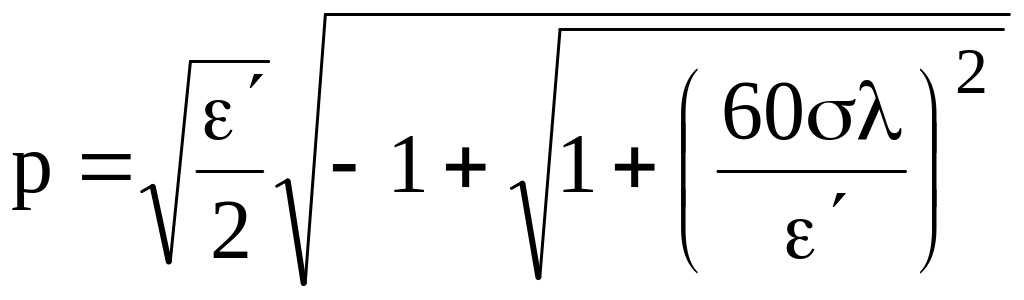 .
(2.8)
.
(2.8)
В некоторых случаях выражения (2.8) можно упростить /2/:
1)
если
>> 60
(т. е. jпр
<< jсм),
то n
![]() ,
p
,
p
![]() ;
(2.9)
;
(2.9)
2)
если
<< 60
(т. е. jпр
>> jсм),
то n
p
![]() .
(2.10)
.
(2.10)
3. Принцип Гюйгенса и зоны Френеля
Определим область пространства, в которой распространяется основная часть радиоволны, формирующая сигнал в точке приёма. Размер и конфигурация такой области определяются принципом Гюйгенса Френеля, согласно которому каждая точка фронта распространяющейся волны, созданной каким-то первичным источником А, сама является источником новой сферической волны (рис. 3.1).
 Полное
поле в точке приема В может быть определено
либо непосредственно как поле первичных
источников, либо путем суммирования
элементарных полей, создаваемых
вторичными источниками, распределенными
по замкнутой поверхности, охватывающей
первичные источники. В теории такой
вторичный источник называется элементарным
источником Гюйгенса, и диаграмма
направленности его излучения имеет
форму кардиоиды (F()
= 0,5 (1 + Cos)).
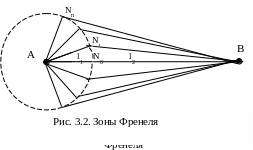
Рассмотрим построение, предложенное
Френелем (рис. 3.2). Пусть в т. А помещён
излучатель, а в т. В – приёмная антенна.
Источник создаёт сферическую волну, т.
е. волну, поверхностью равных фаз которой
является сфера с центром в т. A.
Построим конические поверхности с
вершиной в т. В и осью АВ такие, чтобы
образующие конусов отличались между
собой на величину
Полное
поле в точке приема В может быть определено
либо непосредственно как поле первичных
источников, либо путем суммирования
элементарных полей, создаваемых
вторичными источниками, распределенными
по замкнутой поверхности, охватывающей
первичные источники. В теории такой
вторичный источник называется элементарным
источником Гюйгенса, и диаграмма
направленности его излучения имеет
форму кардиоиды (F()
= 0,5 (1 + Cos)).
Рассмотрим построение, предложенное
Френелем (рис. 3.2). Пусть в т. А помещён
излучатель, а в т. В – приёмная антенна.
Источник создаёт сферическую волну, т.
е. волну, поверхностью равных фаз которой
является сфера с центром в т. A.
Построим конические поверхности с
вершиной в т. В и осью АВ такие, чтобы
образующие конусов отличались между
собой на величину
![]() (m
= 1, 2,…). Тогда должны выполняться следующие
равенства:
(m
= 1, 2,…). Тогда должны выполняться следующие
равенства:
![]() .
(3.1)
.
(3.1)
Пересечение конусов с фронтом волны образует на сферической поверхности семейство коаксиальных окружностей. Участки поверхности сферы, заключённые между смежными окружностями, называются зонами Френеля. Первая, или главная, зона Френеля – часть сферы, ограниченная окружностью N1, зоны высших порядков представляют собой кольцевые области. Из (3.1) следует, что фазы радиоволн, излучаемых виртуальными источниками смежных зон, отличаются в среднем на .
 Разобьём
каждую зону Френеля на большое количество
колец конечной ширины и просуммируем
векторы напряжённости поля в точке
приёма от каждого кольца (рис. 3.3). Пусть
Ei
результирующая амплитуда напряжённости
поля волны в т. приёма от i-й
зоны Френеля. Векторы от соседних зон
направлены в проти-воположные стороны,
т. к. их фазы отличаются на .
С ростом i
амплитуда Ei
будет убывать как за счёт удаления
вторичных источников от т. приёма, так
и потому, что направление максимума их
излучения всё более отклоняется от
направления на точку приёма. Результирующую
амплитуду волн от вторичных источников
всех зон Френеля можно представить в
виде знакопеременного сходящегося ряда
Разобьём
каждую зону Френеля на большое количество
колец конечной ширины и просуммируем
векторы напряжённости поля в точке
приёма от каждого кольца (рис. 3.3). Пусть
Ei
результирующая амплитуда напряжённости
поля волны в т. приёма от i-й
зоны Френеля. Векторы от соседних зон
направлены в проти-воположные стороны,
т. к. их фазы отличаются на .
С ростом i
амплитуда Ei
будет убывать как за счёт удаления
вторичных источников от т. приёма, так
и потому, что направление максимума их
излучения всё более отклоняется от
направления на точку приёма. Результирующую
амплитуду волн от вторичных источников
всех зон Френеля можно представить в
виде знакопеременного сходящегося ряда
![]() (3.2)
(3.2)
Обычно расстояние между передающей и приёмной антеннами значительно превышает длину волны, т. е.
l1 + l2 >> . (3.3)
Тогда амплитуды Ei
от соседних зон мало отличаются друг
от друга и можно считать, что
![]() ,
т. е. выражения в скобках в (3.2) близки к
нулю. Таким образом, в результате взаимной
компенсации сигналов от соседних зон
высших порядков результирующая амплитуда
поля от всех зон Френеля
,
т. е. выражения в скобках в (3.2) близки к
нулю. Таким образом, в результате взаимной
компенсации сигналов от соседних зон
высших порядков результирующая амплитуда
поля от всех зон Френеля
![]() ,
т. е. эквивалентна излучению половины
первой зоны Френеля (реально полной
компенсации соседних зон не происходит,
поэтому более точно
,
т. е. эквивалентна излучению половины
первой зоны Френеля (реально полной
компенсации соседних зон не происходит,
поэтому более точно
![]() ).
В первом приближении полагают, что
поверхность первой зоны Френеля и есть
область пространства, ответственная
за создание сигнала в точке приёма.
).
В первом приближении полагают, что
поверхность первой зоны Френеля и есть
область пространства, ответственная
за создание сигнала в точке приёма.
 Зоны
Френеля могут быть построены на
поверхности произвольной формы. Найдём
радиус n-й
зоны Френеля на плоскости S,
перпендикулярной направлению
распространения, в предположении, что
распространяется плоская радиоволна.
Согласно обозначениям рис. 3.4,
Зоны
Френеля могут быть построены на
поверхности произвольной формы. Найдём
радиус n-й
зоны Френеля на плоскости S,
перпендикулярной направлению
распространения, в предположении, что
распространяется плоская радиоволна.
Согласно обозначениям рис. 3.4,
![]() .
(3.4)
.
(3.4)
Если выполняется условие l1, l2 >> , то
![]() ,
,
![]() .
(3.5)
.
(3.5)
Подставив выражения (3.5) в (3.4), нетрудно получить
![]() .
(3.6)
.
(3.6)
Зафиксируем на плоскости S, перпендикулярной трассе AB, точки образующей n-й зоны Френеля и будем перемещать S вдоль трассы (рис. 3.5). Из (3.4) следует, что в этом случае выполняется равенство

![]() .
(3.8)
.
(3.8)
Математически (3.8) есть уравнение эллипса, следовательно, границы зон Френеля в пространстве представляют собой поверхности эллипсоидов вращения с фокусами в точках А и В. Области пространства между двумя соседними эллипсоидами называют пространственными зонами Френеля. Максимума радиус сечения эллипсоида плоскостью S достигает при l1 = l2 = AB/2:
![]() .
(3.9)
.
(3.9)
 Экспериментально
существование зон Френеля подтверждается,
например, изменчивостью в точке приёма
B
напряжённости поля, создаваемого
источником в т. A,
при изменении радиуса R
отверстия в условно бесконечном экране
(рис. 3.6). В полном соответствии с принципом
Гюйгенса сложение сигналов от неперекрытых
еще зон Френеля приводит к колебаниям
сигнала. Другой пример приведён в разделе
7.
Экспериментально
существование зон Френеля подтверждается,
например, изменчивостью в точке приёма
B
напряжённости поля, создаваемого
источником в т. A,
при изменении радиуса R
отверстия в условно бесконечном экране
(рис. 3.6). В полном соответствии с принципом
Гюйгенса сложение сигналов от неперекрытых
еще зон Френеля приводит к колебаниям
сигнала. Другой пример приведён в разделе
7.
