
- •1 .Орташа арифметикалық жылдамдығын, орташа квадраттық жылдамдығын және ең ықтимал жылдамдықтарды анықтайтын өрнектерін салыстырып, осы есептелген үш жылдамдықтар арасындағы байланысты талдаңыз.
- •1.Бірінші текті фазалық ауысулар.Фазалық тепе-теңдік сызығы.Клапейрон- Клаузиус теңдеуі
- •3. Идеал газ күйінің теңдеуі, оның жалпы анықталмаған түрі. Қысымның газдың сандық тығыздығымен байланысы.
- •2.Максвеллдің үлестірілу функциясының жылдамдықтың х –компоненті үшін түрі.
- •3.Жылу молшері. Жылу мөлшерінің процеске катысты анықталуы.
- •1. Изобарлық процестегі жылусыйымдылық. Майер теңдеуі.
- •1.Изохоралық процесс.
- •2. Идеал газдардың жылу сыйымдылығы.
- •3. Заттың құрылымдық элементтері. Зат молшері – моль.
- •2. Температура түсініктемесі. Температуралық шкала, реперлік нүктелер, температураны
- •3.Термодинамиканың 2 бастамасы жане оның физикалық мағынасы.
- •3.Еркіндік дәрежелер саны. Газдардың жылусыйымдылығы арасындағы қатынастар
- •3.Энергияның тең үлестірілу заңы.
- •2. Термодинамиканың екінші бастамасының статистикалық сипаты. Энтропияның физикалық мағынасы
- •3.Материялық денелердің молекула-кинетикалық моделі. Атомдар мен молекулалар массасы.
- •1. Зат қасиеттерінің құрылымы мен моле-дың жылулық қозғалыспен байланысы.
- •1. Карно циклі. Карно циклінің пайдалы әсер коэффициенті. Карно теоремасы.
- •3. Молекулааралық өзара әрекеттесу күштері. Алыстан және жақыннан әсерлесу күштері. Күштердің молекулааралық қашықтыққа тәуелділігі.
- •1.Сиретілген газдардағы физикалық құбылыстар
- •3.Молекулааралық өзара әрекеттесу күштері.Күштердің молекулааралық қашықтыққа тәуелділігі.
- •2.Газдардағы еркін жүру жолы мен орташа соқтығысу саны
- •3.Адиабаталық процесстегі жұмыстың формуласы
- •1. Концентрация. Көлемдік, салыстырмалы мольдік, салыстырмалы массалық концентрация.Парциал қысым және оның қоспадағы мольдік үлесімен байланысы. Дальтон заңы
- •3.Идеал газдың ішкі энергиясы. Ішкі энергияның жүйенің күйіне тәуелділігі.
- •1. Адиабаттық процесс. Пуассон теңдеуі.
- •2. Жылудың механикалық жұмысқа айналуы. Циклдік процестер. Цикл жұмысы.
- •3. Жылуөткізгіштік. Фурье заңы. Жылуөткізгіштік коэффициентінің қысым мен температураға тәуелділігі.
- •2.Политроптық процесс.Политроп теңдеуі.
- •1. Политроптық процесс.Политроп теңдеуі.
- •2.Изотермдік процесс.Изотермдік процесс кезіндегі жұмыстың формуласы.
- •3.Тұтқырлық. Ньютонның үйкеліс заңы. Тұтқырлық коэффициентінің қысым мен температураға тәуелділігі.
- •1.Изохоралық процесс.
- •3.Ньютонның үйкеліс заңы. Тұтқырлық коэффициентінің қысым мен температураға тәуелділігі.
1. Изобарлық процестегі жылусыйымдылық. Майер теңдеуі.
Изобарлық
процесс қысым тұрақты
 болғанда өтеді. Изобарлық процестің
мольдік жылу сыйымдылығы
болғанда өтеді. Изобарлық процестің
мольдік жылу сыйымдылығы
 деп белгіле-неді және (6.14)-ші формула
бойынша мынаған тең болады:
деп белгіле-неді және (6.14)-ші формула
бойынша мынаған тең болады: .
(6.22)Тұрақты қысым кезінде газға берілген
.
(6.22)Тұрақты қысым кезінде газға берілген
 жылу мөлшері, оның ішкі энергиясын
өзгертуге және жұмыс істелуіне
жұмсалады:
жылу мөлшері, оның ішкі энергиясын
өзгертуге және жұмыс істелуіне
жұмсалады: .Сондықтан,
жылусыйымдылығы (6.22) өрнегіне сәйкес
мына-ған тең:
.Сондықтан,
жылусыйымдылығы (6.22) өрнегіне сәйкес
мына-ған тең:
 .
(6.23)Бір моль идеал газдың күйінің
теңдеуі
,онда
изобарлық процессте
көлем және
температура өзгереді, демек
.
(6.23)Бір моль идеал газдың күйінің
теңдеуі
,онда
изобарлық процессте
көлем және
температура өзгереді, демек
 ,
себебі
,
себебі
 ,
,
осыдан
(6.23)-ші теңдеудің оң жағындағы екінші
мүше былай анықта-лады:
 .
(6.24)Осы формуланың көмегімен
жылу сыйымдылығы ((6.23) теңдеу) үшін
.
(6.24)Осы формуланың көмегімен
жылу сыйымдылығы ((6.23) теңдеу) үшін
 немесе
немесе
 (6.25)қатысын аламыз.Осы (6.25)-ші өрнектен
тұрақты қысым кезіндегі жылусыйым-дылық
тұрақты көлем кезіндегі жылусыйымдылықтан
(6.25)қатысын аламыз.Осы (6.25)-ші өрнектен
тұрақты қысым кезіндегі жылусыйым-дылық
тұрақты көлем кезіндегі жылусыйымдылықтан
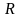 универсал газ тұрақтысына тең шамаға
жоғары екенін көреміз. Олай болса, бір
моль газ бір кельвинге (1К)
тұрақты
қысымда қызғанда, оның жылу-сыйымдылығы
тұрақты көлемдегі жылусыйымдылықтан
универсал газ тұрақтысына тең шамаға
жоғары екенін көреміз. Олай болса, бір
моль газ бір кельвинге (1К)
тұрақты
қысымда қызғанда, оның жылу-сыйымдылығы
тұрақты көлемдегі жылусыйымдылықтан
 -ға
тең істеген жұмысының шамасына үлкен
болады.Осыдан, бір
моль идеал газ изобарлық ұлғайып, бір
кельвинге қызғанда, істеген жұмысының
сандық мәні универсал газ тұрақты-сына
тең болады.(6.20)-шы өрнекті ескеріп,
(6.25)-ші формуланы былай жазамыз:
-ға
тең істеген жұмысының шамасына үлкен
болады.Осыдан, бір
моль идеал газ изобарлық ұлғайып, бір
кельвинге қызғанда, істеген жұмысының
сандық мәні универсал газ тұрақты-сына
тең болады.(6.20)-шы өрнекті ескеріп,
(6.25)-ші формуланы былай жазамыз:
 .(6.26)Универсал
газ тұрақтысының мәні
.(6.26)Универсал
газ тұрақтысының мәні
 Дж/моль, онда
Дж/моль, онда
 қатысы (-әрпімен
белгіленеді) біратомды идеал газ үшін
тұрақты шама, мынаған тең болады:
қатысы (-әрпімен
белгіленеді) біратомды идеал газ үшін
тұрақты шама, мынаған тең болады:
 (6.27)Изобарлық
процесте сыртқы күштердің әсерінен
немесе газ тарапынан сыртқы денелерге
әсер ететін күштердің жұмысы (6.8) теңдеу
бойынша анықталады:
(6.27)Изобарлық
процесте сыртқы күштердің әсерінен
немесе газ тарапынан сыртқы денелерге
әсер ететін күштердің жұмысы (6.8) теңдеу
бойынша анықталады:
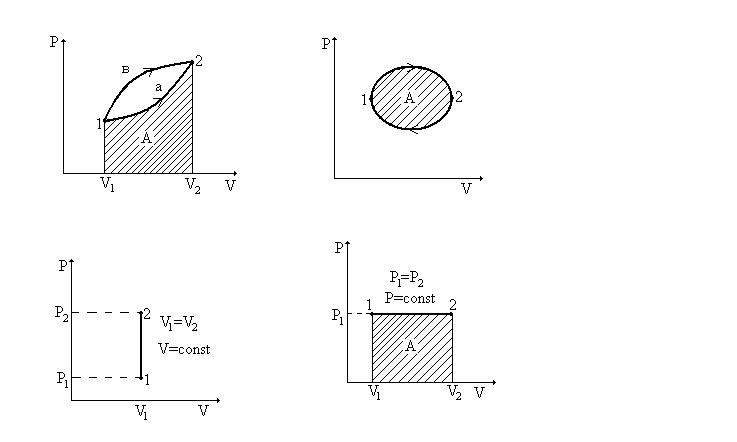
 .
(6.28)Егер
.
(6.28)Егер
 ,
онда
,
онда
 ;
;
 ,
,
 .
6.7-суреттегі
.
6.7-суреттегі
 – диаграммада
– диаграммада
2.
Молекулалардың орташа арифметикалық
жылдамдығын максвеллдің үлестірілу
функциясын қолданып, табыңыз.
Максвеллдік күйдегі газ үшін молекулалық
жылдамдықтың кез кел-ген
 функциясының орташа мәнін (4.6) бойынша
былай анықтайды:
функциясының орташа мәнін (4.6) бойынша
былай анықтайды:

Осы
(4.30)-шы өрнектегі үлестірілу функциясының
орнына (4.29) анықтайтын шамасын қойып,
 деп, оны 0 және
аралығын-дағы мүмкін болатын жылдамдықтар
бойынша интегралдап, орташа
арифметикалық жылдамдықтың
деп, оны 0 және
аралығын-дағы мүмкін болатын жылдамдықтар
бойынша интегралдап, орташа
арифметикалық жылдамдықтың
 мәнін табамыз:
мәнін табамыз:
 мұндағы
мұндағы
 ,
ал
,
ал
 деп белгілесек, онда
деп белгілесек, онда
 түріне келтіріледі. Мұндай интеграл-дардың
мәнін келесі есептеу ережелерін қолданып,
табамыз:
түріне келтіріледі. Мұндай интеграл-дардың
мәнін келесі есептеу ережелерін қолданып,
табамыз:
а)
егер
 -
жұп сан болса, онда
-
жұп сан болса, онда
 ;
(4.31)
;
(4.31)
б) егер – тақ сан болса, онда
 .(4.32)
бойынша
.(4.32)
бойынша
 (4.33)
Егер (4.31)-ге (4.33)-тегі интегралдың өрнегін
қоссақ және есеп-теулер жүргізсек, онда
былай шығады:,
(4.33)
Егер (4.31)-ге (4.33)-тегі интегралдың өрнегін
қоссақ және есеп-теулер жүргізсек, онда
былай шығады:,
 демек
демек
 немесе
немесе
 ,
(4.34) мұндағы
,
(4.34) мұндағы
 –
мольдік масса,
–
мольдік масса,
 – молекула массасы,
– молекула массасы,
![]() –
Авогадро саны, Т
–
температура, R
–
универсал газ тұрақтысы.
–
Авогадро саны, Т
–
температура, R
–
универсал газ тұрақтысы.
(4.34)-ші теңдеу молекуланың орташа арифметикалық жылдам-дығын анықтайды. Газдың белгілі массасындағы молекулалардың орташа арифметикалық жылдамдығы тек температураға тәуелді екен.
Орташа
арифметикалық жылдамдықты
 жылдамдықтың
ком-понентінің
модулінің орташа мәнімен салыстырсақ
((4.26) өрнек), онда ол
жылдамдықтың
ком-понентінің
модулінің орташа мәнімен салыстырсақ
((4.26) өрнек), онда ол
 -дан
екі есе кіші болады, демек
-дан
екі есе кіші болады, демек
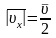 .
(4.35)
.
(4.35)
3.
Молекулалық жүйедегі кездейсоқ шамалар.
Ықтималдық теориясының негізгі ұғымының
біреуі – кездейсоқ шама деген болады.
М/ы, газдың молекуласының v=const болмайды.
Белгілі уақытта молекуланың жыл-н білсек
те, біз оның дәл мәнін 0,01 н/е 0,001 секунд
өткенде неге тең екендігін анықтай
алмаймыз. Молекула жыл-ң өзгерісі
кездейсоқ сипатқа ие, демек кездейсоқ
шамаға жатады. Әр жеке молекула қандай
жылд-пен қозғалады және тап осы кезде
қай жерде болатынын алдын ала болжау
мүмкін емес, өйткені олар кездейсоқ
шама. М-ы су буға айналады (бұны А оқиға
десек) , оны атмосфералық қысымда
 (қыздыру
А оқиғаның болу шарты) ,Демек, әр G
шарттар комплексі іске асырылса, А оқиға
болады.
(қыздыру
А оқиғаның болу шарты) ,Демек, әр G
шарттар комплексі іске асырылса, А оқиға
болады.
Әр G комплекс шарттары жүзеге асырылғанда сөзсіз болатын оқиғаны ақиқатты д.а. Оқиға мүмкін емес, егер оның болмайтынын біле тұра G комплекс шарттары жүзеге асырылса А оқиға кездейсоқ д.а. , егер G комплекс шарттары жүзеге асырылғанда, оның болуы да, болмауы да мүмкін.
№5. билет
