3. Идеал газ күйінің теңдеуі, оның жалпы анықталмаған түрі. Қысымның газдың сандық тығыздығымен байланысы.

Газ күйін сипаттайтын параметрлер арасында байланыс болады. Газдың күйін анықтайтын негізгі параметрлерге газдың қысымы, температурасы және көлемі жатады. Бұл параметрлердің байла-нысын анықтайтын теңдеуді газ күйінің теңдеуі деп атайды. Оның жалпы анықталмаған түрі былай жазылады:

немесе әрбіреуінің қалған екеуіне тәуелділігін ескеріп , немесе деп те жазамыз.

Қысымды анықтайтын молекула-кинетикалық теңдеуін және температураның анықтамасын қолданып, мына фор-муланы аламыз:

Егер газдың массасы өзгермесе, тұрақты болады, онда p қысым температураға пропорционал.

Егер газдың қоспасын алсақ, онда массалары әр түрлі газдардың молекулаларының орташа жылдамдықтары әр түрлі, бірақ орташа энергиясы бірдей болады. Қоспаның қысымы мынаған тең болады:

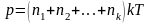, (2.51)

мұндағы – компоненттің бірлік көлемдегі молекулалар саны немесе

(2.52)

мұндағы - – компоненттің парциал қысымы.

(2.52) өрнегі Дальтон заңы деп аталады. Бұл заң идеал газ қоспасының қысымы, сол қоспаны құрайтын компоненттердің парциал қысымдарының қосындысына тең екенін көрсетеді.

Егер 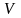көлемде 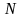молекула болса, онда , осыны ескеріп (2.51) теңдеуді былай жазамыз:

немесе (2.53)

Осы (2.53) теңдеуге үш негізгі күй параметлері , , кіреді, сондықтан бұны газ күйінің теңдеуі деп айтуға болады. Бірақ бұл теңдеуді белгілі зат мөлшері үшін жазу керек, мысалы, бір моль үшін жазсақ, онда 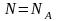, сондықтан

, (2.54)

мұндағы – екі іргелі тұрақтылардың көбейтінідісі универсал газ тұрақтысы деп аталады және R әрпімен белгіленеді, демек

.Оның мәні Дж/мольК.

Универсал газ тұрақтысын ескеріп (2.54)-ші теңдеуді мына түрде жазамыз:

(2.55)

Осы өрнек Менделеев-Клапейрон теңдеуі немесе бір моль идеал газ күйінің теңдеуі деп аталады. Ал газдың кез келген m массасы үшін күй теңдеуі былай анықталады. (2.53) өрнектегі газдың N молекулалар санын, мольдің анықтамасын қолданып, былай жазамыз . Онда (2.53) мына түрде жазылады:

(2.56)

мұндағы – берілген газ массасындағы мольдер саны. (2.55)-ті ескеріп, (2.57)-ні мына түрде жазуға болады:

немесе (2.57)

Осы (2.57) өрнек идеал газдың кез келген m массасы үшін жазылған күй теңдеуі.

№3билет

1.Қысымның физикалық мағынасы. Газ қысымының молекулалардың ілгерілемелі қозғалысының энергия тығыздығымен анықталатынын дәлелдеңіз.Қысым бетке әсер ететін күштің нормаль құраушысының -ке қатынасы арқылы анықталады, демек .

Ньютонның 2-ші заңы бойынша уақыт аралығында 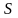ауданға ОХ осі бағытта берілетін импульсті анықтаймыз . Сонымен, уақыт бойынша орташаланған немесе бірлік уақытта қабырғаға берілетін импульстің қосындысы мынаған тең болады:

Қысым бірлік көлемдегі молекулалардың ілгерілемелі қозғалысының кинетикалық энергиясының үштен екісіне тең 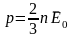. (1) (1) ші теңдеуден тұрақты болғанда, қысым молекуланың ілгерілемелі қозғалысының орташа кинетикалық энергиясына пропор-ционалдығы шығады. екенін ескеріп, осы теңдеуді былай жазамыз: , – газдағы молекуланың толық энергиясы 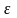– энергия тығыздығы.

Газдағы молекулалар қозғалысын толық сипаттау үшін, олардың өзі орналасқан ыдыстың қабырғасымен соқтығысу мәселесін шешу қажет. Бұл мәселені шешу, біздің алға қойғалы отырған мақсатымыз, газдың ыдыс қабырғаларына түсіретін қысымын және осы қысым сияқты макроскоптық параметрлердің газдың сипаттамаларымен байланысын түсіндіру болып табылады.

Біз идеал газды қарастырамыз. Онда молекулалық күштер ескеріл-мейді, газдың молекулалары материялық нүктелер деп есептеледі. Мұндай молекулалар уақытының басым көпшілігін еркін қозғалыста өткізеді, тек кейде бір-біріне немесе өзі орналасқан ыдыстың қабырға-ларына серпімді соқтығысады. Газ тепе-теңдік күйде, онда барлық -молекулалар жылдамдығы бірдей және декарт координнаттар жүйе-сінің үш осьтері бойымен 1/6 бөлігі оң бағытта, ал 1/6 бөлігі кері бағытта қозғалады, Қозғалыс бағыттарының ықтималдығы бірдей.

Қысым бетке әсер ететін күштің нормаль құраушысының -ке қатынасы арқылы анықталады, демек .Ньютонның 2-ші заңы бойынша уақыт аралығында ауданға ОХ осі бағытта берілетін импульсті анықтаймыз: . Сонымен, уақыт бойынша орташаланған немесе бірлік уақытта қабырғаға берілетін импульстің қосындысы мынаған тең болады:

Қысым бірлік көлемдегі молекулалардың ілгерілемелі қозғалысының кинетикалық энергиясының үштен екісіне тең .(1) (1) ші теңдеуден тұрақты болғанда, қысым молекуланың ілгерілемелі қозғалысының орташа кинетикалық энергиясына пропор-ционалдығы шығады. екенін ескеріп, осы теңдеуді былай жазамыз: ,

– газдағы молекуланың толық энергиясы – энергия тығыздығы.