3.Энергияның тең үлестірілу заңы.

Бір атомды газдың молекуласының әр ілгерілемелі еркіндік дәрежесіне КТ/2 орташа бөлінеді. Егер молекула ілгерілемелі қозғалыстан басқа еркіндік дәрежелерге ие болса, онда Больцман теоремасының тұжырымдамасы бойынша: егер молекулалық жүйе жылулық тепе-теңдікте Т температурада болса, онда молекулалардың орташа барлық еркіндік дәрежелері бойынша бірқалыпты таралған және молекуланың әр еркіндік дәрежесіне лайықты КТ/2-ге энергия тең келеді. Осы теорема еркіндік дәрежелері бойынша кинетикалық энергияның тең үлестірілу заңы немесе энергиялық бірқалыпты үлестірілу заңы деп аталады. Сондықтан газдың ішкі энергиясын және жылусыйымдылығын есептеу үшін оның молекулаларының еркіндік дәрежелер санын білу керек. Жалпы жағдайда екі атомды молекула алты (6) еркінік дәрежелеріне ие болады: 3 ілгерілемелі, 2 айналмалы және бір тербелмелі.

Газдың мольдік жылусыйымдылықтары еркіндік дәрежелері бойынша былай анықталады.

және

Молекуланың iеркіндік дәрежесінің санын есептегенде тербелмелі еркіндік дәрежесін екі еселеу қажет.

№9 билет

1. Диффузия. Фиктің бірінші заңы. Диффузия коэффициенті және қысым мен температураға тәуелділігі.Диффузия процесінде шама -ге немесе -ге тењ, демек i cорт молекулаларыныњ концентрациясына немесе молекула массасына тењ болады. А, О жєне В жазыќтыќтардыњ єрќайсысында немесе єр т‰рлі, сондыќтан массаныњ тасымалдауы байќалады. Егер 8.3 -суреттегі жазыќтыќтар орналасќан кµлемніњ барлыќ жерінде ќысым бірдей, температура т±раќты болса, онда і сорт молекулалардыњ аѓыныныњ тыѓыздыѓы ‰шін (8.12)-ші тењдеуді мына т‰рде жазамыз:

(8.15)

Немесе

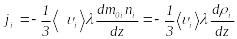. (8.16)М±ндаѓы - і сорт молекулалардыњ сандыќ аѓыныныњ тыѓыз-дыѓы; -і сорт молекулалардыњ массалыќ аѓыныныњ тыѓызды-ѓы; – газ ќоспасыныњ і компонентініњ тыѓыздыѓы; – і сорт (компонентініњ) молекулалардыњ орташа арифметикалыќ жылдамдыѓы; – сандыќ кµлемдік концентрацияныњ градиенті; – массалыќ тыѓыздыќтыњ градиенті.

Егер (8.15) жєне (8.16)-шы тењдеулердегі жєне градиенттері бірге тењ болса, онда осы градиенттердіњ алдындаѓы про-порционалдыќ коэффициенттіњ сандыќ мєні і сорт молекулалардыњ аѓыныныњ тыѓыздыѓына тењ, демек:

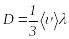, (8.17)м±ндаѓы D – диффузия коэффициенті деп аталады. (8.17)-ден D µлшем бірлігі м²/с-ќа тењ болатыны шыѓады.

Осы (8.17)-ні ќолданып (8.15) жєне (8.16)-шы тењдеулерді мына т‰рде жазамыз: 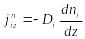, (8.18)

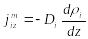(8.19)Сонымен газ ќоспасындаѓы диффузиялыќ аѓын немесе , немесе концентрация градиентіне тура пропорционал жєне оѓан ќарсы баѓытта µтеді: , ,(8.20)

,м±ндаѓы – і компоненттіњ салыстырмалы концентрациясы; - і компоненттіњ парциалдыќ тыѓыздыѓы; - і компоненттіњ пар-циалдыќ диффузия коэффициенті.

Диффузиялыќ аѓын векторлыќ шама, сондыќтан былай аныќ-талады: , (8.21)

м±ндаѓы – масса аѓыныныњ тыѓыздыѓы, – газдыњ массалыќ тыѓыздыѓы, D – диффузия коэффициенті.бДиффузия коэффициенті сан жаѓынан 1с уаќытта бірлік аудан арќылы градиенті бірге тењ болѓанда µтетін диффузия аѓынына тењ.

(8.18)-(8.21) µрнектерді Фиктіњ бірінші зањы деп атайды. Б±л зањды А.Фик 1855 ж. ашќан.

(8.17)-ші формулада белгілі температурада т±раќты, , ал . Сондыќтан, т±раќты температурада диффузия коэффициенті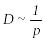 , (8.22)

демек ќысымѓа кері пропорционал µзгереді. Екінші жаѓынан, белгілі ќысымда , ал . Олай болса, т±раќты ќысымда диффу-зия коэффициентініњ температураѓа тєуелділігі

(8.23)т‰рінде аныќталады.

Осы ќорытындылар эксперименттік зерттелді. Диффузия коэффи-циентініњ температураѓа тєуелділігініњ дєрежесі ((8.23) формула) бір-сыпыра газдар ‰шін эксперимент бойынша жоѓары болады. Ал тыѓыз газдарда диффузия коэффициентініњ ќысымѓа кері пропорцио-налдыѓы орындалмайды.

2.Сәйкестік күйлер заңы. Ван-дер-Ваальстің келтірілген теңдеуі. Жеке заттың өзіне тән қасиеттері Ван-дер-Ваальстің теңдеуіне a және b тұрақтылары мен , , критикалық параметрлері арқылы кіреді. Сондықтан, мысалы, әр түрлі газдардың изотермдерін бірдей тұрақты температурада келтірсек, олардың түрлері әр түрлі болады. Идеал газдың изотермдерінің барлық газдар үшін айырмашылығы жоқ, себебі газдың қасиеттеріне тәуелсіз.

Жан-жақты (универсалды) заттың табиғатына тәуелсіз нақты газдың күй теңдеуін Ван-дер Ваальстің теңдеуі бойынша табуға болады. Ол үшін p, V, T күй параметрлерінің сәйкес критикалық , , шамаларға қатысын қолданады, демек: , , , (5.31)мұндағы – келтірілген параметрлер деп аталады. Бұл өлшемсіз шамалар сәйкес критикалық параметрлерінің үлесі ретінде анықталған нақты газ параметрлерінің мәндері.Ван-дер-Ваальстің теңдеуіндегі

p, V, T-ның орнына -ны қойып және a мен b тұрақ-тыларын (5.30)-шы формула бойынша , , көмегімен түрлендіріп, келесі теңдеуді аламыз: немесе . (5.32)Бұл формула кез келген заттың келтірілген параметрлерін байла-ныстырады, жеке заттың қасиеттерін сипаттайтын тұрақтылар кірмей-ді, сондықтан (5.32)-ші теңдеу универсалды, барлық заттарға бірдей.(5.32)-ші теңдеу Ван-дер-Ваальстің келтірілген күй теңдеуі деп аталады. шамалардың әр түрлі заттарға бірдей мәндерінің жиынтығы сәйкестік күйлерін анықтайды. Егер үш келтірілген параметрлердің екеуі әр түрлі заттарда бірдей болса, онда үшінші параметріде осы заттарда бірдей. Осы заң сәйкестік күйлер заңы деп аталады.

Ван-дер-Ваальс теңдеуіне күйлері бағынатын заттар, сәйкестік күйлер заңын қанағаттандырады (қамтамасыз етеді), сондықтан термодинамикалық ұқсас болады. Термодинамикалық ұқсас заттар үшін мына қатыс орындалады:

(5.33)Осыдан барлық заттар үшін бұл қатынастың мәні бірдей болуға тиіс, ал дұрысында нақты, тығыз әр түрлі газдар үшін қатынастың осы мәнінен ауытқулар байқалады.

Сөйтіп, сәйкестік күйлер заңының орындалуының шарты термо-динамикалық ұқсас заттар үшін

,(5.34)демек осы комплекс бірдей болуы қажет.

3. Температуратураның молекула-кинетикалық теория тұрғысынан мағынасы. Больцман тұрақтысы Температураның анықтамасы және қысыммен байланысы. Жүйенің жылулық тепе-теңдік күйіне өту процесі температураның теңестірілуімен байланысты және тепе-теңдік күйге жеткенде, жүйе-нің барлық бөліктерінің температурасы және қысымдары бірдей болады.

Сондықтан, жүйеде жылулық тепе-теңдік орналасу процесінде теңелетін шама – температура. (2.33) теңдеуі бойынша жүйедегі бөл-шектердің тығыздығы n тұрақты болса, газдың V көлеміндегі массасы өзгермейді, онда газды қыздыру (немесе суыту) кезінде, тек оның молекулаларының орташа кинетикалық энергиясы өзгеруі мүмкін. Жылу алмасу процесінде температураның теңелуі, газдағы молекула-лардың орташа кинетикалық энергиясының теңелуін білдіреді.

Осыдан, тепе-теңдік күйге өту кезінде, газдың бір бөлігінен екіншісіне энергия беріледі, бірақ тұтас дене ретінде алынған барлық газдың энергиясы теңелмейді, оның тек бір молекулаға қатысты орташа кинетикалық энергиясы теңеліп отырады, демек (2.34) өрнек бойынша …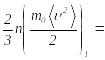

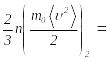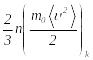
теңдігін аламыз. Мұндағы – газдың бөліктері.

Осыдан, молекуланың орташа кинетикалық энергиясының өзгерісі температураның өзгерісін сипаттайтыны анық, шынында, бұл энергия температура болып саналуы тиісті. Температура сияқты, молекуланың орташа кинетикалық энергиясы аддитивтік шама емес.

Осындай көз карасқа сұйеніп, молекулалардың ілгерілемелі қозғалысының орташа кинетикалық энергиясын температура ретінде қарастырып,  деп белгілеп, былай жазамыз: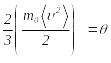 .Соңғы(2.45) өрнекті ескерсек, (2.34) теңдеу келесі қарапайым түрде жазылады: (2.46)Бұл анықтамадағы  температураның өлшем бірлігі градус болуы тиіс. Онда (2.45)-тегі энергияның өлшемін градусқа ауыстыратын коэффициентті кіргізуіміз қажет. Энергияның өлшем бірлігін ауыстыратын коэффициентті – деп белгілейді, температураның белгісі . Сондықтан, -ға тең болады, осыны ескере отырып, (2.45)-ші теңдеуді мына түрде жазуға болады: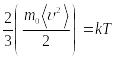 .Осыдан 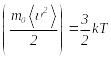(2.47) Бұл теңдеу материялық нүкте деп қарастырып отырған бір молекуланың ілгерілемелі қозғалысының орташа кинетикалық энер-гиясын анықтайды. Оның орташа квадраттық жылдамдығы кеңіс-тік координаттары бойынша үш құраушыларға жіктелуі мүмкін. Молекулалық қозғалыс хаосты, сондықтан молекуланың энер-гиясы осы жылдамдықтар құраушылары бойынша біркелкі үлестірі-леді, демек әрбіреуіне энергия мөлшері бөлінеді. Мұндағы –көбейткіш энергия өлшемі Дж (джоуль) мен температура өлшемі К (кельвин) арасындағы қатынасты білдіреді, Больцман тұрақтысы деп аталады. Оның мәні тәжірибе арқылы тағайындалған. СИ жүйесінде мынаған тең болады:

Дж/К (2.48) (2.47)-ші формула бойынша температура нолге тең болғанда, молеку-лалардың хаосты ретсіз қозғалысының орташа кинетикалық энергиясы ноль болады, демек молекулалардың хаосты қозғалысы тоқталады. Осы температура абсолюттік ноль, демек абсолюттік температуралық шкаланың бастапқы санақ басы болады.Осыған орай, (2.47)-ден теріс таңбалы температура болмайтынын көреміз. Бірақ кейбір жүйелерді сипаттау үшін теріс таңбалы температура ұғымын қолданады, оның тепе-теңдік күйге қатысы жоқ және абсолюттік температурадан төмен деп айтуға болмайды.Сонымен, температура молекулалардың қозғалысының орташа кинетикалық энергиясы бойынша анықталады, ол қысым сияқты статистикалық шамаларға жатады. Сондықтан, бір молекуланың температурасы, немесе молекула “суық”, немесе “ыстық” деген мағынасыз болады.

№10 билет

1.Бірінші текті фазалық ауысулар.Фазалық тепе-теңдік сызығы.Клапейрон- Клаузиус теңдеуіФазалық ауысу,фазалық түрлену — кең мағынасында сыртқы жағдайлар (температура, қысым, магниттік және электрлік өріс, т.б.) өзгергенде заттың бір фазадан екінші фазаға ауысуы; тар мағынасында сыртқы параметрлер үздіксіз өзгергенде физикалық қасиеттердің секірмелі өзгеруі. Температураның, қысымның немесе қандай да бір басқа физ. шаманың Фазалық ауысу өтетін мәні ауысу нүктесі деп аталады. Фазалық ауысудың екі тегін ажыратады. Бірінші текті Фазалық ауысуда заттың тығыздығы, құраушыларының концентрациясы сияқты термодинамикалық сипаттамалары секірмелі түрде өзгереді; масса бірлігінде Фазалық ауысу жылуы деп аталатын жылудың толық анықталған мөлшері бөлінеді немесе жұтылады.  Екінші текті Фазалық ауысу кезінде қандай да бір нөлге тең физикалық шама ауысу нүктесінің бір жағынан екінші жағына қарай ығысу нүктесінен алыстағанда нөлден бастап біртіндеп өседі. Мұнда тығыздық үздіксіз өзгереді, жылу бөлінбейді және жұтылмайды. Бірінші текті Фазалық ауысу табиғатта кең таралған құбылыс. Оған булану мен конденсаттану, балқу мен қатаю, қатты фазаға сублимациялану мен конденсаттану, қатты денелердегі кейбір құрылымдық ауысулар, мысалы, темір-көміртек қорытпасында мартенситтің түзілуі жатады. Таза асқын өткізгіштерде жеткілікті күшті магнит өрісі асқын өткізгіштік күйден қалыпты күйге бірінші текті Фазалық ауысутуғызады. Екінші текті Фазалық ауысуға: макроскоп. магниттік моменттің пайда болуымен бірге жүретін пара-ферромагнетик. ауысу, пара-антиферромагнетик. ауысу, т.б. жатады. Фазалық ауысу температураның, т.б. шамалардың қатаң анықталған мәндеріндегі бөлшектер санына шек қойылмайтын жүйеде ғана өтетін құбылыс.  

Күй диаграммалары.

 

Егер жүйе бір компонентті болса, яғни химиялық біртекті зат немесе қосылыс болса, онда фаза түсінігі агрегаттық күй түсінігімен дәл келеді.Фазалық айналуды көрнекті көрсету үшін диаграммалық күйпайдаланылады. Онда  координатында фазалық өтудің температура мен қысым арасындағы тәуелділік қисықтық түрінде берілген  булану, КБ – балқу және  - сублимация, олар өріс диаграммасын сәйкес қатты (ҚД), сұйық (С) және газ тәрізді (Г) фазаларына келетін үш аймаққа бөледі.Диаграммадағы қисықтық фазалық тепе-теңдік қисықтық деп аталады, оның әрбір нүктесі екі қатар жүзеге асқан фазалардың тепе-теңдік шарттарына сай келеді.Үштік нүкте деп фазалық тепе-теңдіктің қисықтығы қиылысатын нүктені айтады. Сонымен ол заттың үш фазасының бір мезгілде тепе-теңдікте қатар жүзеге асуы шартын анықтайды ( температурасы,  қысым).Судың үштік нүктесіне 273,16К (немесе 0,01⁰С) сәйкес келеді және термодинамикалық температуралық шкаланы тұрғызу үшін негізгі реперлік нүкте болып саналады.

Клапейрон – Клаузиус теңдеуі. 

Клапейрон – Клаузиус теңдеуі  тепе-теңдік қисықтығының көлбеулігін анықтайды. Мұндағы  - фазалық өтудің жылуы (мысалы балқу кезінде – меншікті балқу жылуы).

- зат көлемінің бірінші фазадан екінші фазаға өтуі кезіндегі өзгеруі (мысалы, балқу кезінде – Т _бал балқу температурасы). және  барлық уақытта оң, сондықтан тепе-теңдік көлбеулігі  -дің таңбасымен анықталады. Булану және сублимация кезінде көлем барлық уақытта артады, сондықтан  .Көптеген заттардың

балқуы кезінде көлем артады, сонымен  , яғни қысымның артуы балқу температурасының артуына әкеледі (тұтас сызық КБ- суретте).Көптеген заттар үшін (су,  , шойын) сұйық фазаның көлемі қатты фазаның көлемінен аз болады, яғни  . Сонымен қысымның артуы балқу температурасының төмендеуі мен жүреді (суреттегі штрихталған сызық).

2. Адиабаттық процесс. Пуассон теңдеуі.Адиабаттық процесте газ қоршаған денелерге жылу бермейді және сырттан жылу алмайды. Сондықтан, адиабаттық процесс қоршаған ортамен жылу алмасусыз өтеді, . Термодинамиканың бірінші бастамасы бұл жағдайда былай жазылады: ; немесе dA= -dU.

Осыдан, газдың көлемі өзгергендегі істелетін жұмыс ішкі энергия-ның өзгерісіне әкеледі, демек газдың температурасының өзгеруіне. (6.43)-ші теңдеудегі минус таңба газдың көлемінің ұлғаюы температу-раның төмендеуімен, ал сығылуы – температураның көтерілуімен өтетінін көрсетеді.

Б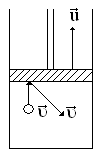 ірінші жағдайда газ жұмысты өзінің ішкі энергиясы есебінен істейді, сондықтан оның тем-пературасы төмендейді. Онда ішкі энергиясының өзгеруі , ал істелген жұмыс . Екінші жағдайда жұмысты сыртқы күштер істейді және осы жұмыс есебінен ішкі энергиясы өседі, демек газдың температурасы көтеріледі. Бұл кезде , ал жұмыс теріс таңбалы, .Температураның бұндай өзгерісін келесі тәжі-рибе бойынша түсіндіруге болады. Жылжымалы поршеньді цилиндрдің ішінде газ орналасқан делік (6.12-сурет). Поршень жылдамдықпен жоғары көтерілгенде, газ ұлғаяды. Поршеньнің қозғалыс бағытында жылдамдықпен молекула ілесе қозғалады делік. Егер молекуланың ыдыстың қабырғасына қатысты жылдамдығы болса, онда поршеньге қатысты оның жылдамдығы . Молекула поршеньмен серпіле соқтығысып, кері шағылады. Поршеньге қатысты молекуланың жыл-дамдығы өзгермейді, бірақ поршеньмен соқтығысқан ыдыстың қабыр-ғасына қатысты кері қайтқан молекуланың жылдамдығы болады. Сондықтан,қозғалыстағы поршеньмен соқтыққан барлық молекулалар одан серпімді шағылып, соқтығысу алдындағы жылдам-дықтан кіші жылдамдықпен кері қайтарылады. Осы молекулалардың орташа жылдамдығының кемуі, газдың температурасының төмендеуі-не әкеледі.Сондықтан, керісінше газ сығылғанда, поршень кері қайтқанда, температура өседі.Пуассон теңдеуі. Адиабаттық процестегі газ күйінің теңдеуі.Адиабаттық процесте газдың қысымы мен көлемінің өзгерісі Бойль-Мариотт заңына бағынбайды. Бұл процесте температура өзгеріп отырады. (6.43) бойынша . (6.44)Бұл теңдеуді шешу үшін -ның өзгерісін анықтау қажет. Идеал газ күйінің теңдеуін қолданып, осы теңдеуді дифферен-циалдап ,температураның өзгерісі -ны анықтаймыз: . (6.45)

(6.44)-ші өрнекке -ның осы мәнін қойып: , -дің орнына, оның мәнін ауыстырып, келесі өрнекті аламыз: . (6.46)

Жылусыйымдылықтар қатысын қолданып, (6.46)-шы формуланы мына түрде жазамыз:

(6.47)Егер (6.47)-дегі тұрақты болса, онда осы теңдеуді былай жазуға болады: Бұл теңдеуді интегралдап, мына түрге келтіреміз: . (6.48)Ақырында потенциалдасақ, сонда (6.48) өрнекті былай жазуымыз-ға болады: .(6.49)

(6.49)-ші теңдеу адиабаттық процесс кезінде идеал газдың көлемі өзгергенде қысымымен көлемінің арасындағы тәуелділікті тағайын-дайды. Бұл өрнек Пуассон теңдеуі немесе адиабаттық процестегі идеал газ күйінің теңдеуі деп аталады, мұндағы –адиабаттық көрсеткіш деп аталады.

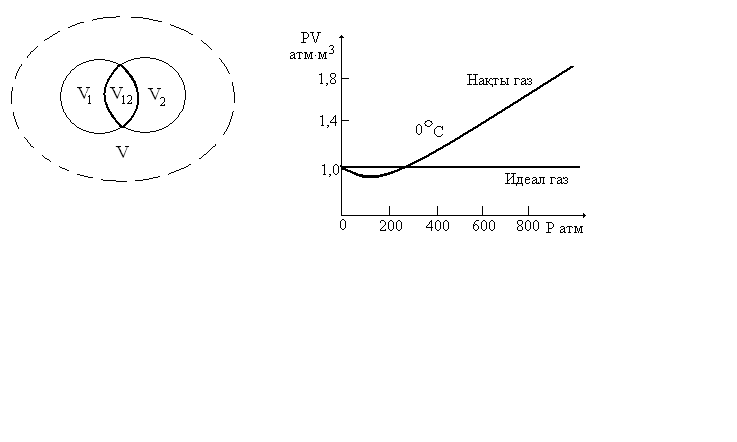
3.Газдардың идеал күйден ауытқуы. Нақты газдың тәуелділігінің графигін сызып, талдаңыз. Бойль-Мариотт, Гей-Люссак, Шарль заңдары жеткілікті сиретілген және идеал газдардың күйін ғана қанағаттанарлық сипаттайды. Нақты газдар қарапайым идеал газ заңдарына бағынбайды, бірақ өте төменгі тығыздықтарда және химиялық реакциялар жоқ кезінде олардың қасиеттері идеал газдыкіне жуық болады. Нақты газдардағы молекула-ларды материялық нүктелер деп қарастыруға болмайды. Оның моле-кулаларының арасында өзара әрекет тебіліс және тартылыс күштері бар, сондықтан мұндай нақты газдың күйі идеал газ күйінің теңдеуінен ауытқиды..Идеал газдың көлемі мен қысымының көбейтіндісі белгілі тұрақты температурада қысымға байланысты өзгермейді, тұрақты болады (5.1-сурет, үзік сызықтар). p-V-T эксперимент нәтижелері бойынша нақты газдың тәуелділігі күрделі болады. 0⁰С температурадағы азоттың эксперименттік изотермдері тұтас сызықпен көрсетілген. Мұнда қысым артқан сайын елеулі ауытқулар байқалады. Осы идеалдықтан ауытқу қысым өскен сайын ұлғаяды. Идеал газ заңдарынан ауытқулар барлық нақты газдарда байқалады, сонымен қатар олардың өздеріне тән өзгешеліктері бар, себебі әрбір газдың моле-кулаларының өлшемдері және молекулалық өзара әрекеттесулері әр түрлі.

Нақты газдың молекулаларының көлемінің ықпалын келесі мысалдан көруге болады. Газдың молекулаларын диаметрі қатты сфера деп қарастырайық. Осы «биллиард шарлары» тәріздес молекулалар көлемі V жәшікте орналасқан делік. Онда жәшіктегі бірінші молекуланың центрі көлемде ғана қозғала алады, өйткені ол ыдыстың қабырға-сына қашық жақын бара алмайды.

№11

1.Шарль заңы. p T диаграмасында p f Tтәуелділік графигі. Қысымның термдік коэффициенті Изохоралық процесс. Көлемі тұрақты жүйеде өтетін процесс ( ) изохоралық (гректің isos – тең, бірдей және chora – кеңіс-тік) процесс деп аталады. Бұл процесс көлемі өзгермейтін жабық ыдыстарда орналасқан газбен сұйықтарда өтеді. Идеал газда изохора-лық процесс кезінде қысымның температураға тәуелдігін Шарль заңы деп атайды.

(2.55)-ші идеал газ күйінің теңдеуінен изохора теңдеуі былай анықталады: , немесе . (2.63)(2.63)-ші Шарль заңы бойынша тұрақты көлемде газдың қысымының температураға байланысты өзгеруі кезінде қатысы өзгермейді.

диаграмасында (2.7-сурет) әр түрлі көлемдер үшін тәуелділік графигі берілген. Идеал газ изохоралары координаттар осьтерінің басынан шығатын түзу сызықтар болады.Изохоралық процестегі идеал газдың қысымының термдік коэффициенті былай анықталады:

(2.64)Б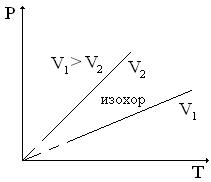 ұл теңдеу күй теңдеуі бойынша анықталады: ; , , сондықтан Идеал газдың температуралық шка-ласы осы заң бойынша негізделген.

Жоғары қысымдардағы тәжірибе-лер нәтижелері идеал газ заңдарынан нақты газ қасиеттерінің ауытқуын көр-сетеді. Газ заңдары кинетикалық тео-риядан бұрын тәжірибе нәтижелерін жалпылау негізінде тағайын-далған, сондықтан теориялық қорытындыларының дұрыстығының дәлелдемесі болады. Бұл заңдар идеал газ үшін дәл орындалады, демек газдың идеалдығын белгілейді. Сондықтан, Бойль-Мариотт, Гей-Люссак немесе Шарль заңдарына бағынатын газды идеал деп атайды.