3.4. Порівняння графіків перехідних функцій, отриманих за аналітичним розв’язком та числовим методом.
а) по рівню h1.
Для перевірки правильності аналітичного розв’язку диференційного рівняння (3.11) побудую в одній системі координат графік залежності (3.12) та графік імпульсної перехідної функції, отриманий за допомогою функції IMPULSE. Послідовність команд, яку потрібно виконати для побудови графіків, зібрана у script-файлі perehidnaH.m.
%perehidnaH1
t=[0:10];
har_riv;
h=C(1)*exp(k(1)*t)+C(2)*exp(k(2)*t);
sys=ss(a,b,c,d);
[y,tt,x]=impulse(sys,[0:1e-3:10]);
figure(1);
plot(tt,x(:,1),'k-',t,h,'ok');grid;
title('impulsna perexidna f');
ylabel('h1,m');xlabel('time,sec');
figure(2);
r=C(1)/k(1)*(exp(k(1)*t)-1)+C(2)/k(2)*(exp(k(2)*t)-1);
sys=ss(a,b,c,d);
[y,tt,x]=step(sys,[0:1e-3:10]);
plot(tt,x(:,1),'k-',t,r,'ok');grid;
title('perehidna f');
ylabel('h1,m');xlabel('time,sec');
В результаті отримуємо графіки:
Рисунок 3.1. Графіки порівняння імпульсної перехідної функції,одержаної:
«o»- за аналітичною залежністю; «-» - із застосуванням функції IMPULSE.
Рисунок 3.2. Графіки порівняння перехідної функції,одержаної:
«o»- за аналітичною залежністю; «-» - із застосуванням функції STEP.
б) по рівню h2.
Для перевірки правильності аналітичного розв’язку диференційного рівняння (3.15) побудую в одній системі координат графік залежності (3.16) та графік імпульсної перехідної функції, отриманий за допомогою функції IMPULSE. Послідовність команд, яку потрібно виконати для побудови графіків, зібрана у script-файлі perehidnaT.m.
%perehidnaH2
t=[0:10];
har_riv2;
h=C(1)*exp(k(1)*t)+C(2)*exp(k(2)*t);
sys=ss(a,b,c,d);
[y,tt,x]=impulse(sys,[0:1e-3:10]);
figure(1);
plot(tt,x(:,2),'k-',t,h,'ok');grid;
title('impulsna perexidna f');
ylabel('h2,m');xlabel('time,sec');
figure(2);
r=C(1)/k(1)*(exp(k(1)*t)-1)+C(2)/k(2)*(exp(k(2)*t)-1);
sys=ss(a,b,c,d);
[y,tt,x]=step(sys,[0:1e-3:10]);
plot(tt,x(:,2),'k-',t,r,'ok');grid;
title('perehidna f');
ylabel('h2,m');xlabel('time,sec');
В результаті отримуємо графіки:
Рисунок.3.3. Графіки порівняння імпульсної перехідної функції,одержаної:
«o»- за аналітичною залежністю; «-» - із застосуванням функції IMPULSE.
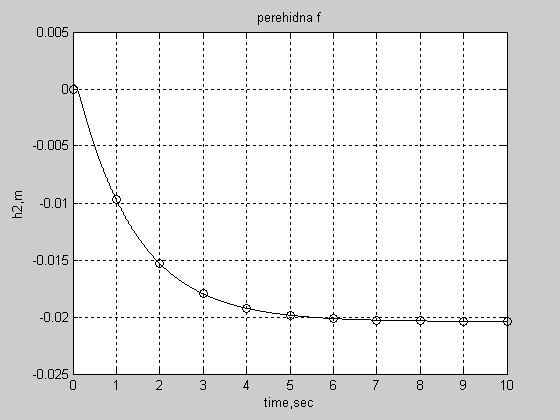
Рисунок 3.4 Графіки порівняння перехідної функції,одержаної:
«o»- за аналітичною залежністю; «-» - із застосуванням функції STEP.
3.2 Аналітичні вирази для визначення реакції системи на вхідний синусоїдальний сигнал ( ) за допомогою інтеграла згортки
Реакцію системи (аналітичний її
вираз) на вхідний сигнал
знайдемо за допомогою
iнтеграла згортки:
Використовуючи інтегрування частинами, знайдемо аналітично інтеграл
тоді
Отже, остаточно
а) по рівню h1.
б) по рівню h2.
Порівнюю графіки, отримані за допомогою аналітичних виразів та з допомогою функції MatLab LSIM. Відповідні програми знаходяться у файлі zgortka:
%zgortka
clc
zapnuli;
h1=yy(1); h2=yy(2);
liner;
sys=ss(a,b,c,d);
w=0.2;
t=[0:100];
U=sin(w*t);
y1=lsim(sys,U,t);
A0=a11*a22;
A1=-a11-a22;
A2=1;
B0=-b11*a22;
B1=b11;
h0=B1/A2;
h0p=B0/A2-(A1*B1)/A2^2;
k=roots([A2 A1 A0]);
%constant
AA=[1 1;k(1) k(2)];
H=[h0;h0p];
C=AA^(-1)*H;
s1=C(1)*(w*exp(k(1)*t)-(w*cos(w*t)+k(1)*sin(w*t)))/(w^2+k(1)^2)+C(2)*(w*exp(k(2)*t)-(w*cos(w*t)+k(2)*sin(w*t)))/(w^2+k(2)^2);
plot(t,s1,'-k',t,y1,'ok');grid;
ylabel('h1,m');xlabel('time,sec');
A0=a11*a22;
A1=-a11-a22;
A2=1;
B0=-b21*a11+b11*a21;
B1=b21;
h0=B1/A2;
h0p=(B0-A1*h0)/A2;
k=roots([A2 A1 A0]);
%constant
A=[1 1;k(1) k(2)];
H=[h0;h0p];
C=AA^(-1)*H;
w=0.2;
s2=C(1)*(w*exp(k(1)*t)-(w*cos(w*t)+k(1)*sin(w*t)))/(w^2+k(1)^2)+C(2)*(w*exp(k(2)*t)-(w*cos(w*t)+k(2)*sin(w*t)))/(w^2+k(2)^2);
c=[0 1];
sys=ss(a,b,c,d);
y2=lsim(sys,U,t);
figure(2);
plot(t,s2,'-k',t,y2,'ok');grid;
ylabel('h2,m');xlabel('time,sec'); Запустивши програму на виконання, одержимо:
Рисунок 3.5. Графіки порівняння перехідних процесів по рівню h1
при дії вхідного сигналу u=sinωt, одержані:
«-»- за аналітичною залежністю; «o» - із застосуванням функції LSIM.
Рисунок 3.6. . Графіки порівняння перехідних процесів по рівню h2
при дії вхідного сигналу u=sinωt, одержані:
«-»- за аналітичною залежністю; «o» - із застосуванням функції LSIM.