6. Определение параметров точности зубчатого колеса

По заданным значениям чисел зубьев (z_k = 110), модуля (m_k = 2 мм) и направлению зуба определяем диаметр делительной окружности зубчатого колеса:

d_k = m_k · z_k = .

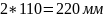Вычисляем другие геометрические элементы колеса:

d_е = d_k + 2,0 · m_k = 220+2*2=224 мм.

d_i = d_k – 2,5 · m_k = 220-2.5*2=215 мм.

b = (0,25÷1,0) · d_п, принимаем b = 0,5 · d_п = 0.5*65=32.5 мм.

d_ст = 1,5 · d_п + 10 = 1.5*65+10=107.5 мм.

l_ст = (0,8÷1,5)∙d_п, принимаем l_ст = 1,0 ∙ d_п = 1.0*65=65 мм;

с = 0,3 ∙ b = 0.3*32.5=9.75 мм;

t = 2,5∙m_k + 2 = 2.5*2+2=7 мм.

Из таблиц выбираем соответственно:

- шероховатость поверхностей по параметру Ra: зубьев – 0.4-0.8 мкм; посадочной поверхности колеса – (0.8-1.6) мкм; рабочей поверхности паза втулки – (0.4-0.8);

- биение торца – 24 мкм (для 7-й степени точности по нормам контакта зубьев).

Назначаем поля допусков на размеры элементов d_е; b; d_ст; l_ст:

d_е = 224h 14; b = 33h 12;

d_ст = 108h 14; l_ст = 65h 12.

Из задания известны также степени точности по нормам кинематической точности, плавности работы, контакта зубьев – 8, а также вид бокового зазора – с.

Выполняем чертеж колеса в соответствии с требованиями ЕСКД (рис. 9). Выбираем из табл.соответствующие контролируемые параметры зубчатого колеса, а затем назначаем средства контроля:

- по нормам кинематической точности: допуск на радиальное биение зубчатого венца F_r = 50 мкм контролировать на биенемере;

- по нормам плавности работы: предельное отклонение шага f_pt = 16 мкм контролировать на шагомере БВ-5004;

- по нормам контакта зубьев: пятно контакта: по высоте ПК 45 %, по длине ПК 60 %, контролировать на обкаточном станке (“по краске”);

- по боковому зазору: наименьшее смещение исходного контура E_HS = 120 мкм и допуск на смещение исходного контура T_H = 120 мкм контролировать с помощью тангенциального зубомера №1 ЛИЗ.

7. Расчет размерной цепи.

В соответствии с заданием необходимо выполнить расчет размерной цепи, образованной размерами звеньев B₁, B₂, B, B₃, и B_Δ, где B₁­­ – высота крышки подшипника, B₂­­ – толщина кольца проставочного, B – ширина кольца подшипника, B₃­­ – глубина гнезда корпуса, B_Δ­­ – размер под прокладку. Так как количество звеньев небольшое, расчет выполняем методом максимума минимума, начиная с решения первой задачи: когда известны номинальные значения и предельные отклонения составляющих звеньев и необходимо определить параметры замыкающего звена. Из задания известны также диаметральные размеры d_п (внутреннего) и d₂ (наружного) колец подшипника. По данным находим ширину B кольца подшипника. В данном случае B = мм. В соответствии с табл. назначаем поля допусков на составляющие звенья (для шестого класса подшипника) по IT7, причем, для B₁ и B, по основному валу h8, для B₃ – основному отверстию H8. Находим предельные отклонения размеров составляющих звеньев B₁, B₂ и B₃ по табл., ширины B кольца подшипника по табл..

Верхние предельные отклонения звеньев B₁, B₂ и B равны нулю, звена B₃ – E_S (B₃) = + 46 мкм, нижние предельные отклонения звеньев, мкм:

E_i (B₁) = – 33 мкм;

E_i (B₂) = – 22 мкм;

E_i (B) = – 150 мкм;

E_i (B₁) = 0.

Тогда пользуясь формулами, определим:

предельные размеры составляющих звеньев, мм:

B_{1 max} = 19; B_{2 max} = 7; B_max = 33; B_{3 max} = 58,046;

B_{1 min} = 18,967; B_{2 min} = 6,978; B_min = 32,850; B_{3 min} = 58;

B₁ = 19_-0.033; B₂ =7_-0.022; B = 33_-0.150; B₃ = 58^+0.046;

допуски размеров составляющих звеньев, мкм:

ТB₁ = 33; ТB₂ = 22; ТB = 150; ТB₃ = 46.

Построим схему плоской сборочной размерной цепи (рис. 10).

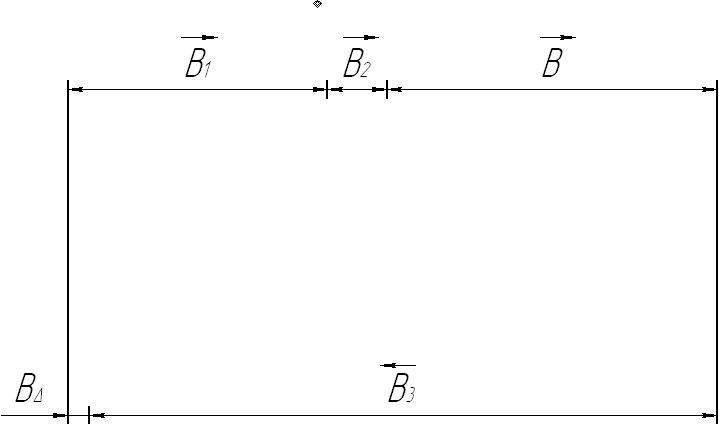
Рисунок 10 – Схема плоской сборочной схемы

Как видно из рис. 10, звенья B₁, B₂ и B являются увеличивающими, а звено B₃ – уменьшающим. Определим параметры замыкающего звена. Вычислим, пользуясь приведенными в соотношениями:

номинальное значение замыкающего звена по формуле

= (19+7+33) – 58 = 1 мм;

предельные размеры замыкающего звена по формулам

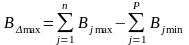= (19+7+33) – 58 = 1 мм;

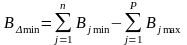= (18,967+6,978+32,850) – 58,046 = 0,749 мм

предельные отклонения замыкающего звена по формулам

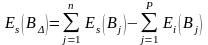= 0 – 0 = 0;

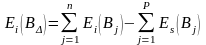=[(-0,033)+(–0,022)+(–150)]–0.046= -0.251мм;

допуск замыкающего звена по формуле

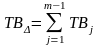= 0.150+0.033+0.022+0.046 = 0.251 мм,

что соответствует IT14 = 0.251 мм.

Таким образом, размер замыкающего звена (при заданных номинальных размерах и предельных отклонениях составляющих звеньев) может быть выполнен с точностью B_Δ = 1_-0.251 мм.

Если принять, что рассеяния предельных отклонений размеров звеньев цепи (рис. 10) подчиняются закону нормального распределения, величины размахов полностью вписываются в поля допусков, а кривые распределения симметричны относительно середины полей допусков, то применяя теоретико-вероятностный метод расчета и формулу, определим допуск замыкающего звена

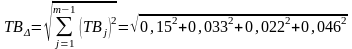= 0.162 мм,

что приблизительно равно IT13 = 0.14 мм. При решении по методу максимума-минимума 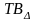= 0.089 мм, т.е. на 70 мкм или 65 % больше, чем вероятностном методе расчета. В случае же сохранения TB = 0.089 мм можно значительно расширить допуски размеров составляющих звеньев TB₁, TB₂, TB и TB₃.