12.5.2 Расчет косозубой цилиндрической передачи на прочность

Прочность зуба косозубого колеса определяется его формой, раз­мерами в нормальном сечении и длиной зуба. Чтобы унифицировать методику расчетов на прочность прямых и косых зубьев, введено по­нятие эквивалентного колеса. При расчетах на прочность косозубые колеса условно заменяют эквивалентными по прочности цилиндри­ческими прямозубыми. Эквивалентным прямозубым колесом называ­ют такое колесо, форма и размеры зубьев которого приближенно сов­падают с формой и размерами зубьев косозубого колеса в нормальном сечении. При этом модуль m_v эквивалентного колеса и нормальный модуль т_п косозубого колеса равны, как и длины зубьев этих колес (b= ,а радиус делительной окружности эквивалентного колеса ра­вен наибольшему радиусу кривизны эллипса, полученного в сечении делительного цилиндра косозубого колеса плоскостью п-п (рис. 12.17). Полуоси полученного в сечении эллипса равны c=d/2 и e=d/(2cos ), где d—диаметр делительной окружности косозубого колеса; — угол наклона зуба.

Из аналитической геометрии известно, что наибольший радиус кривизны эллипса равен /c=d/(2 . Тогда диаметр дели­тельного цилиндра эквивалентного колеса

d_v =2r_v =d/cos² ,

а число зубьев эквивалентного колеса

где d , z — соответственно диаметр делительного цилиндра и число зубьев косозубого колеса.

Приведенный радиус кривизны суммарная длина контактных линий l= .

Вывод зависимостей для проведения прочностных расчетов цилиндрических косозубых колес аналогичен прямозубым. Наклонное рас­положение зубьев придает косозубым колесам и передачам ряд поло­жительных свойств, в том числе повышенные прочность и плавность, что учитывают при расчетах. В связи с этим при определении изгибных напряжений вводят учи­тывающий наклон зуба коэффициент

)

где коэффициент осевого перекрытия; b — ширина венца (рис. 12.17); р_х =p_t /sin — осевой шаг.

Тогда уравнение для проверочных расчетов косозубых колес на сопротивление усталости при изгибе примет вид

где — коэффициент прочности зуба (выбирается в зависимости от эквивалентного числа зубьев z_v ); m_n — нормальный модуль косозубо­го колеса.

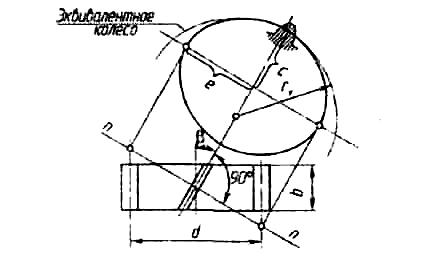
Рис. 12.17

При расчете косозубых колес по контактным напряжениям наклон зуба учитывается коэффициентом формы сопряженных поверхностей и коэффициентом, учитывающем суммарную длину контактных ли­ний,

Z_H

= .

12.6 Конические зубчатые передачи

Для передачи вращательного движения между валами, оси кото­рых пересекаются под некоторым углом Σ, применяют конические зубчатые колеса (рис. 12.18). Они бывают с прямым, косым или винто­вым зубом. Преимущественно применяют прямо­зубые конические колеса и только тогда, когда нельзя использовать цилиндрические. Это объясняется большей сложностью изготовле­ния и сборки конических передач. Одно из колес конических передач из-за пересечения осей валов располагается консольно, что создает дополнительные трудности при конструировании опор. Кроме того, валы и опоры нагружаются не только радиальными, но и осевыми си­лами. Применение более сложных опор приводит к снижению КПД и большему шуму, чем при использовании цилиндрических передач.

С точки зрения движения зацепление конических колес можно представить как перекатывание друг по другу без проскальзывания конусов, соприкасающихся по образующим. Эти конусы называют начальными, вершины их должны находиться в точке пересечения геометрических осей колес и при монтаже это необходимо обеспе­чить. Различают также: делительные конусы, являющиеся базовыми для определения элементов зубьев и их размеров; конусы вершин, ограничивающие зубья со стороны, противоположной телу зубчатого колеса; конусы впадин, отделяющие зубья от тела колеса. При изго­товлении конических колес исправление высоты зубьев практически отсутствует, поэтому начальный и делительный конусы совпадают. Углы делительных конусов колес обозначают и , а межосевой угол — ( = + ); чаще всего он равен 90°.

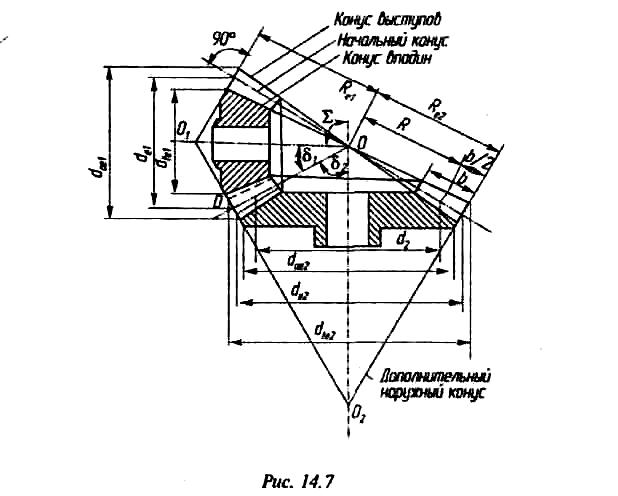
Рис. 12.18

В коническом колесе размеры зубьев рассматривают не в торцо­вом сечении, а в сечении поверхностью дополнительного конуса, ось которого совпадает с осью колеса, а образующие перпендикулярны к образующим делительного конуса.

Окружности диаметром d₁ (), полученные в результате пересе­чения делительных и дополнительных конусов шестерни (колеса), называются делительными окружностями конических колес. По этим окружностям определяется модуль зацепления конических колес. Его назначают из конструктивно-технологических условий изготовления и сборки или по данным расчета на прочность. Зубчатый венец огра­ничивается внешним и внутренним торцами. Зубья конических колес (имеют переменные высоту и толщину. Стандартизированы размеры зубьев, их модуль и шаг по наружному торцу, они обозначаются с ин­дексом е (т_е, р_е, d_e, d_ae, d_fe).

Передаточное отношение i конической передачи определяют из условия качения без проскальзывания начальных конусов: i= d₂ / d₁ = sin ₂ / sin ₁ или при 90° i = tg ₂ = ctg ₁. Передаточное число и для кинематических передач рекомендуется принимать не бо­лее 7,5, для силовых — не более 6,3 (и =

Геометрический расчет конической передачи (см. рис. 12.18) ведут по следующим зависимостям: внешний делительный диаметр колеса d_e = z; углы делительных конусов колес ₂ =arctgi, ₁ = 90°- ₂ ; внешнее конусное расстояние R_e =m_e z/(2 sin ) ; ширина зубчатого венца b= (0,25...0,3)R_e или b=(4...10)m_е; среднее конусное расстояние R = R_e-0,5b; средний окружной модуль m=m_eR/R_e; внешняя высота головки зуба h_ae = т_е; внешняя высота ножки зуба h_fe = (1 + с* )т_е, где коэффициент радиального зазора с* =45 при т_е 0,5, с* = 0,3 при 0,5<m_е <1 и с* =0,2 при т_е 1,0; внешний диаметр вершин зубьев d_ae =d_e + 2h_ae cos ; внешний диаметр впадин зубьев d_fe =d_e -2h_fe cos .

При прочностных расчетах расчетным является средний модуль т, по которому вычисляется внешний модуль т_е.

Конические колеса малых размеров (d_e < 70 мм) изготавливают со сплошным диском (рис. 12.19, а). При большихдиаметрахдля сниже­ния массы и момента инерции в диске колеса предусматривают выточ­ки, отверстия (рис. 12.19, б). Ступицу колеса располагают с противопо­ложной стороны делительного конуса. Колеса с обратной ступицей (рис. 12.19, в) можно применять при условии, если ступица не выступа­ет за пределы конуса впадин, что необходимо для выхода инструмента при нарезке зубьев.

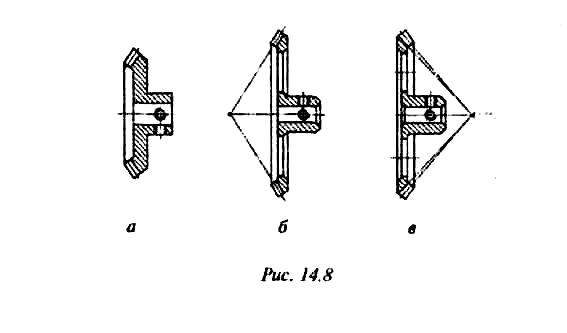
Рис. 12.19

Зубчатые колеса изготавливают из сталей 35,45, 50. При требова­ниях малой массы и небольших нагрузках для изготовления применя­ются сплавы Д16Т, В95Т и пластмассы — текстолит марки ПТК, ка­прон. Колеса из пластмассы обеспечивают бесшумность работы.