
- •Оглавление
- •10.1 Общие сведения…………………………………………………………....69
- •12.4.6 Проверочный и проектировочный расчет прямозубой
- •Введение
- •1 Машины и механизмы, их структура и классификация
- •1.1 Звенья и кинематические пары механизмов
- •1.2 Кинематические цепи. Степень подвижности механизмов
- •1.3 Классификация механизмов
- •2 Основы расчетов деталей механизмов и машин на прочность
- •2.1 Деформации и напряжения. Метод сечений
- •2.2 Простейшие типы деформации стержней
- •2.3 Допущения, принимаемые при расчетах на прочность
- •3 Растяжение-сжатие стержней. Свойства материалов
- •3.1 Определение деформаций и напряжений при растяжении – сжатии
- •3.3 Твердость материалов
- •4 Сдвиг и кручение
- •4.1. Напряжения и деформации при сдвиге
- •4.2 Статические моменты сечения. Центр масс сечения
- •4.3 Моменты инерции сечений
- •4.4 Понятие о крутящем моменте
- •5 Изгиб прямолинейного стержня
- •5.1 Понятия о деформации изгиба
- •5.2 Определение нормальных напряжений при изгибе
- •5.3 Определение деформаций при изгибе
- •6 Сложные сопротивления. Местные напряжения
- •6. 1 Понятие о теориях прочности
- •6.2 Изгиб с кручением стержней круглого поперечного сечения
- •6.3 Концентрация напряжений
- •6.4 Контактные напряжения
- •7 Устойчивость сжатых стержней
- •7.1 Устойчивость равновесия сжатого стержня
- •7.2 Определение критической силы. Задача Эйлера
- •8 Прочность при циклически изменяющихся напряжениях
- •8.1 Понятие об усталости материалов
- •8.4 Факторы, влияющие на предел выносливости
- •9 Основы триботехники
- •9.1 Общие сведения
- •9.2 Трение и изнашивание
- •10 Основные принципы и правила конструирования
- •10.1 Общие сведения
- •10.2 Стандартизация и унификация
- •10.3 Прочность и жесткость
- •10.4 Точность взаимного положения деталей
- •10.5 Другие методы и принципы конструирования
- •11 Конструкционные и смазочные материалы
- •11.1 Требования к конструкционным материалам
- •11.2 Черные металлы
- •11.2.1 Чугуны
- •1.2.2 Стали
- •11. 3.1 Медь и ее сплавы
- •11. 3.2 Алюминий и его сплавы
- •11.3.3 Сплавы титана и магния, баббиты
- •11.4 Пластмассы
- •11. 5 Смазочные материалы
- •12 Механические передачи
- •12.1 Характеристики механических передач
- •12.2 Фрикционные механизмы
- •12.2.1 Общие сведения
- •12.2.2 Кинематика фрикционных механизмов
- •12.2.3 Расчет фрикционных передач
- •12.3 Ременные передачи
- •12.3.1 Кинематика, геометрия и силы в ременных передачах
- •12.3.2 Порядок расчета
- •12.4 Зубчатые механизмы. Прямозубые цилиндрические передачи
- •12.4.1 Параметры цилиндрических прямозубых колес
- •12.4.2 Конструкции и материалы зубчатых колес
- •12.4.3 Виды повреждений зубьев
- •12.5 Особенности цилиндрических косозубых передач
- •12.5.2 Расчет косозубой цилиндрической передачи на прочность
- •12.6 Конические зубчатые передачи
- •12.6.1 Силы, действующие в зацеплении конической передачи
- •12.6.2 Расчет конической передачи на прочность
- •12.7 Передачи с круговинтовым зацеплением Новикова
- •12.8 Планетарные и волновые зубчатые передачи
- •12.8.1 Планетарные механизмы
- •12.8.2 Волновые зубчатые передачи
- •12.9 Червячные передачи
- •12.10 Механизмы винт-гайка
- •12.11 Цепные передачи
- •12.11.1 Конструкции приводных цепей
- •12.11.2 Расчеты цепных передач
- •12.12 Рычажные передачи
- •13 Валы и оси
- •13.1 Конструкции валов и осей
- •13.2 Расчеты валов и осей
- •14 Опоры осей и валов
- •14.1 Требования, предъявляемые к опорам
- •14.2 Подшипники скольжения
- •14.3 Подшипники качения
- •15 Муфты
- •15.1 Назначение и классификация муфт
- •15.2 Постоянные муфты
- •15.3 Управляемые муфты
- •15.4 Самоуправляемые муфты
- •16 Корпуса
- •17 Упругие элементы
- •18 Соединения деталей
- •19 Динамика механизмов
12.5 Особенности цилиндрических косозубых передач
В
косозубых цилиндрических колесах в
отличие от прямозубых оси
зубьев составляют некоторый угол ![]() с осью колеса (рис. 12.15). Величину
этого угла рекомендуют выбирать равной
10, 12, 16 и 20°. Работать
в паре могут колеса только с равными
углами наклона зубьев, но
с разным (правое и левое) направлением
винтовых линий. Оси косозубых
колес параллельны.
с осью колеса (рис. 12.15). Величину
этого угла рекомендуют выбирать равной
10, 12, 16 и 20°. Работать
в паре могут колеса только с равными
углами наклона зубьев, но
с разным (правое и левое) направлением
винтовых линий. Оси косозубых
колес параллельны.
Косозубые передачи обладают рядом достоинств по сравнению с прямозубыми: благодаря наличию угла наклона зубья вступают в зацепление по своей длине b постепенно, что обеспечивает более равномерную и плавную работу и, естественно, снижение шума механизма вследствие большего коэффициента перекрытия. У косозубых колес минимальное число зубьев zкmin, при котором не происходит подрезания, меньше, чем у прямозубых (zкmin = zmin cos3 β) . Косозубые передачи позволяют подобрать при заданном межосевом расстоянии за счет изменения угла наклона β пару колес со стандартным модулем.
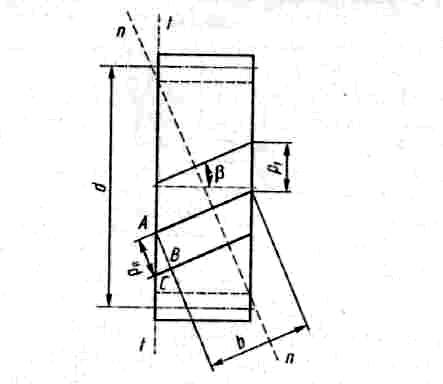
Рис. 12.15
К недостаткам косозубых передач следует отнести более сложное изготовление колес по сравнению с прямозубыми и появление дополнительного осевого усилия, передаваемого на опоры. Для устранения осевого усилия можно применять шевронные зубчатые колеса. Венец шевронного колеса состоит из участков с правым и левым направлением зубьев. Зубья такого колеса могут быть нарезаны на одном ободе или венец колеса должен состоять из жесткого соединения двух косозубых колес с разным направлением наклона зубьев. Шевронные колеса в изготовлении сложнее, чем косозубые.
Различают
торцовое сечение в плоскости t
-t
вращения
колеса и
нормальное п-п-
в
плоскости,
перпендикулярной к направлению зуба.
Параметры, определяющие размеры косозубых
колес в обоих сечениях, не одинаковы,
поэтому им присваивают разные индексы:
параметрам в торцовом сечении — t,
в нормальном — п.
Окружной
шаг
АС
(рис.
12.15) в торцовом сечении
=
mt,
а в нормальном сечении
шаг АВ
равен
рп
=
тп,
где mt
и
т„
— соответственно
торцовый и нормальный модули. Из ![]() АВС
следует,
что рt
=рп
/ cos
,
поэтому
АВС
следует,
что рt
=рп
/ cos
,
поэтому
![]() .
.
При
нарезании косозубых колес ось инструмента
наклоняют по отношению
к оси колеса на угол
.
Стандартными являются нормальный модуль
тп
и
размеры профиля зуба в нормальном
сечении (рп
=
тп,
ha
=mn
, ,
=(1
+ c*)mn
, h=(2+с*)тп
,
s=nmn
/2).
Модуль mt
в
торцовой
плоскости, окружной шаг
,
диаметр
делительной (базовой) окружности
d
=mt
z
косозубого
колеса зависят от угла
наклона продольных
осей зубьев. Размеры косозубого колеса,
выраженные через стандартный модуль,
следующие: делительный диаметр d=mnz/
cos![]() ;
диаметр
выступов зубьев da=d
+ 2тп;
диаметр впадин df
=
d-(2+2c*)тп;
длина зуба b=(3...15)тп;
ширина венца колеса b'=bcos
.
Отметим,
что ширина венца колеса влияет на
значение коэффициента перекрытия,
как и угол наклона
;
диаметр
выступов зубьев da=d
+ 2тп;
диаметр впадин df
=
d-(2+2c*)тп;
длина зуба b=(3...15)тп;
ширина венца колеса b'=bcos
.
Отметим,
что ширина венца колеса влияет на
значение коэффициента перекрытия,
как и угол наклона![]() зуба.
зуба.
12.5.1 Силы, действующие в зацеплении косозубой цилиндрической передачи
В
косозубых цилиндрических колесах (рис.
12.16) продольные, оси
симметрии зубьев составляют с направлением
образующей цилиндра
угол
.
Сила полного давления
,
воспринимаемая зубом в
месте зацепления, направлена по нормали
к его рабочей поверхности. Она лежит
в плоскости n-n,
нормальной к продольной оси зубьев,
перпендикулярна к соприкасающимся
профилям зубьев в точке касания,
совпадает с линией зацеплением и может
быть разложена по трем
взаимно перпендикулярным направлениям.
В плоскости п
-п ее
раскладывают
на составляющую Fr
(радиальная
сила), направленную по
радиусу к центру колеса, и силу ![]() ,
лежащую в
плоскости п-п
и
перпендикулярную к силе Fr,
которую, в свою очередь, раскладывают
на осевую силу Fa,
направленную
параллельно геометрическим осям
колес, и окружную силу Ft
направленную
перпендикулярно к
геометрическим осям колес.
,
лежащую в
плоскости п-п
и
перпендикулярную к силе Fr,
которую, в свою очередь, раскладывают
на осевую силу Fa,
направленную
параллельно геометрическим осям
колес, и окружную силу Ft
направленную
перпендикулярно к
геометрическим осям колес.
Окружная сила
Ft =2TK/d=2TK/(mtz)=2TKcos /(mnz),
где
Т-
передаваемый
момент; К
=
![]() Ка
- коэффициент,
учитывающий
распределение нагрузки по ширине венца
(
),
внутреннюю
Ка
- коэффициент,
учитывающий
распределение нагрузки по ширине венца
(
),
внутреннюю
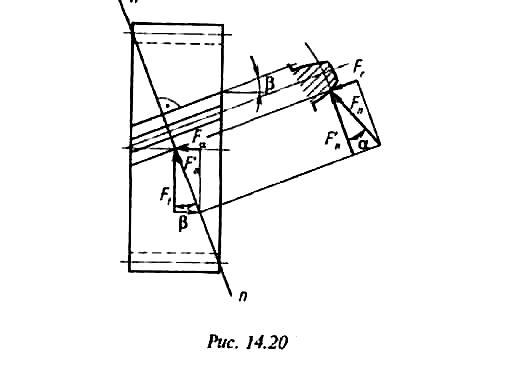
Рис. 12.16
динамику передачи (Kv) и распределение нагрузки между зубьями ( ).
Силу Fn в зацеплении косозубых колес выразим через окружную силу:
Fn
=
/(cos![]() cos
).
cos
).
Радиальная и осевая силы, нагружающие валы и опоры передачи, соответственно равны:
Fr
=
tg
/cos
;
![]() =
tg
.
=
tg
.
