5 Изгиб прямолинейного стержня

5.1 Понятия о деформации изгиба

Изгиб вызывается внешними силами, направленными перпен­дикулярно к продольной оси стержня, а также парами внешних сил, плоскость действия которых проходит через эту ось (рис. 5.1, а). При действии такой нагрузки продольная ось стержня искривляется. В по­перечных сечениях стержня при изгибе возникают моменты внутрен­них сил, плоскость действия которых перпендикулярна к плоскости сечения, т.е. изгибающие моменты .

Если изгибающий момент в поперечном сечении является един­ственной составляющей внутренних сил, изгиб называется чистым.

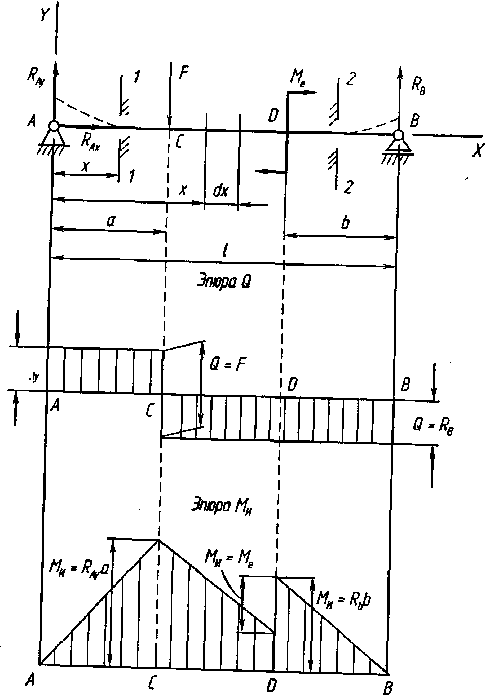
Рис. 5.1

Изгиб называют поперечным, если в поперечных сечениях вместе с изгибающим моментом возникают и поперечные силы . Попе­речный изгиб встречается в реальных условиях нагружения чаще чис­того изгиба.

Если плоскость действия изгибающего момента Ми проходит че­рез центр масс поперечного сечения, т.е. через любую центральную ось сечения, изгиб называют простым или плоским, а если не прохо­дит, — косым. При плоском изгибе продольная ось стержня и после деформации остается в плоскости внешних сил, т.е. представляет со­бой плоскую кривую линию. При косом изгибе плоскость деформа­ции не совпадает с плоскостью внешних сил. Косой изгиб относится к деформациям, называемым сложными.

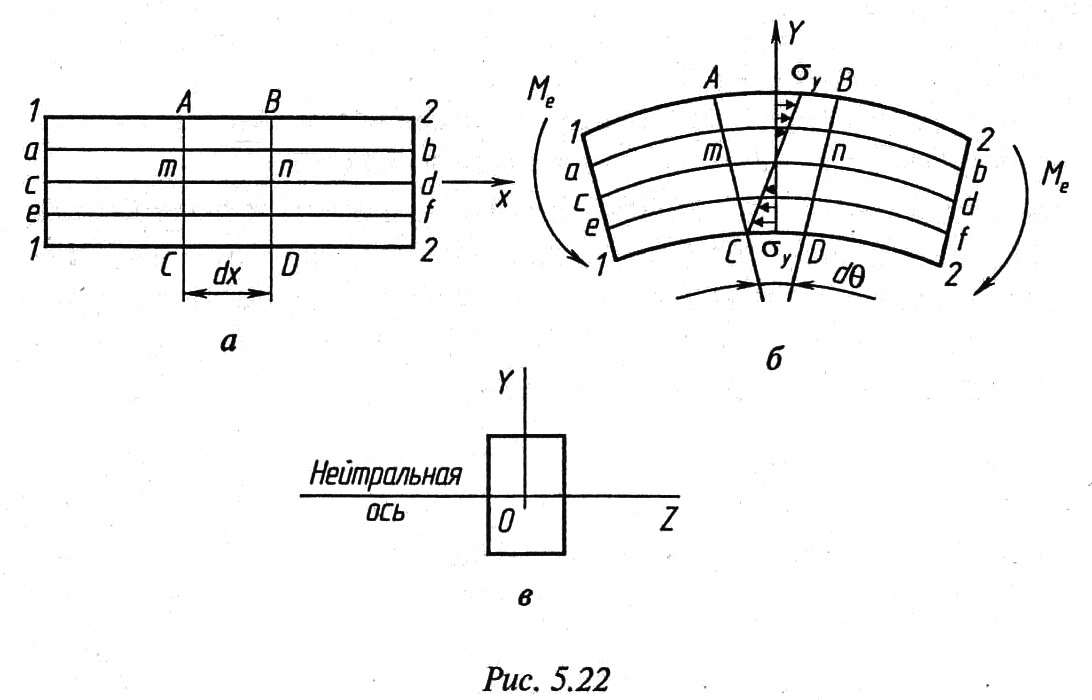
Рис. 5.2

5.2 Определение нормальных напряжений при изгибе

Рассмотрим прямолинейный стержень постоянного поперечно­го сечения прямоугольной формы (рис. 5.2, а), который изгибается (рис. 5.2, б) под действием двух внешних моментов приложен­ных в плоскости XOY к его концам. При таком нагружении в попереч­ных сечениях присутствуют только изгибающие моменты, т.е. стер­жень испытывает чистый изгиб. Если до деформации на боковую поверхность стержня нанести координатную сетку (рис. 5.2, а), то при изгибе заметим следующее (рис. 5.2, б): линии сетки, параллель­ные оси стержня, изогнутся, сохранив между собой прежние расстоя­ния, причем на выпуклой стороне (ab) удлинятся, что свидетельствует об их растяжении, а на вогнутой (ef) станут короче; линии 1—1 и 2-2, перпендикулярные к оси стержня, останутся прямыми, но наклонят­ся относительно друг друга.

Будем считать, что поперечные сечения, плоские до деформа­ции, останутся плоскими и после деформации. При переходе от рас­тянутой части изгибаемого стержня к сжатой имеется слой (cd), не ис­пытывающий при изгибе ни сжатия, ни растяжения. Он называется нейтральным слоем. Линия пересечения нейтрального слоя с плоскостью поперечного сечения стержня называется нейтральной осью. Как видно, волокна стержня деформируются различно. Выделим элемент стержня, ограниченный двумя поперечными сечениями, находящи­мися на бесконечно малом расстоянии друг от друга. При изгибе сечения АС и BD повернутся относительно друг друга на угол . Во­локно , принадлежащее нейтральному слою (рис. 5.2, б), сохра­нит свою первоначальную длину , а волокно АВ, отстоящее на рас­стоянии у от нейтрального слоя, будет иметь длину . Радиус кривизны дуги изогнутой оси стержня можно считать постоянным. Отно­сительная деформация волокна

прямо пропорциональна расстоянию у от него до нейтрального слоя,

где — радиус кривизны нейтрального слоя (изогнутой оси).

При чистом изгибе касательные напряжения отсутствуют в попе­речных сечениях стержня. Предполагается, что продольные волокна не давят друг на друга, они испытывают одноосное растяжение или сжатие. Зависимость, полученная на основании этого предположения, дает результаты, хорошо согласующиеся с данными экспериментов.

Согласно закону Гука, для растяжения или сжатия в слое, отстоя­щем на расстоянии у от нейтрального слоя, напряжение

.

Из этого уравнения видно, что нормальные напряжения отсутст­вуют в нейтральном слое и максимальны в волокнах, наиболее уда­ленных от него. Но так как не известны ни ρ, ни положение нейтраль­ного слоя, эта формула в инженерных расчетах не применяется.

Свяжем действующие в точках сечения напряжения с внутренни­ми силами поперечного сечения при чистом изгибе. Используя метод сечений, определим, что не только поперечные силы , но и продоль­ная сила отсутствуют, т.е. . Элементарная продольная сила в сечении, действующая на площадку , равна а сумма таких сил по сечению — . Но

, так как рассматривается изогнутый стержень, радиус кривиз­ны оси которого ; следовательно, . Данный интеграл равен статическому моменту поперечного сечения относительно ней­тральной оси (рис. 5.2, в). Так как он равен нулю, нейтральная ось (OZ) проходит через центр масс сечения. Координата в выражении для получает определенность, она равна расстоянию до оси, проходящей через центр масс поперечного сечения.

Изгибающий момент в сечении . При заданной плоско­сти действия момента внешних сил изгибающий момент равен мо­менту внутренних сил в этой же плоскости, т.е. относительно ней­тральной оси. Выразим изгибающий момент через элементарные внутренние силы . При принятом направлении осей , а полный изгибающий момент

где — момент инерции сечения относительно нейтральной оси; — радиус кривизны изогнутого нейтрального слоя. Выразим из последнего уравнения кривизну нейтрального слоя:

Подставив это значение в выражение для σу, получим зависимость

,

позволяющую определять нормальные напряжения в любой точке се­чения стержня по известным изгибающему моменту Ми и моменту инерции сечения Iz относительно оси, проходящей через центр масс сечения.

Из последнего выражения видно, что нормальные напряжения для нейтрального слоя, когда у =0, равны нулю, а максимальные нор­мальные напряжения будут в наиболее удаленных от нейтрального слоя волокнах (рис. 5.2, б), когда у = у тах. При расчетах на прочность представляют интерес прежде всего наибольшие по величине напря­жения. В поперечном сечении они равны

,

где — осевой момент сопротивления сечения (момент со­противления при изгибе). Он является геометрической характеристи­кой поперечного сечения стержня, влияющей на его прочность при изгибе. Для стержней с прямоугольным сечением со сторонами и момент сопротивления , а для стержней с круглым поперечным сечением диаметром .