4.2 Статические моменты сечения. Центр масс сечения

При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций за­висит только от площади поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при расчетах сжатых стержней на устойчивость, прочность и жесткость элементов конст­рукции зависят также от формы их поперечного сечения. К числу геометрических характеристик сечения, учитывающих его размеры, форму и влияющих на прочность и жесткость конструкций, относят­ся статические моменты, моменты инерции и моменты сопротивле­ния сечения.

Статическим моментом сечения S относительно любой оси на­зывается взятая по всей площади сечения сумма произведений пло­щадей п элементарных площадок и их расстояний до этой оси. Так, статический момент сечения (рис. 4.2) относительно оси OZ

где n — число элементарных площадок сечения; Ai — площадь эле­ментарной i-й площадки сечения, расположенной на расстоянии yi , от оси OZ.

При → 0 и n → ∞

где — элементарная площадка.

Размерность статических моментов — длина в кубе. Статические моменты могут быть положительными, отрицательными и равными нулю.

Считая, что поверхностная плотность сечения постоянна, координаты центра масс сечения , можно выразить через стати­ческие моменты:

Аналогично

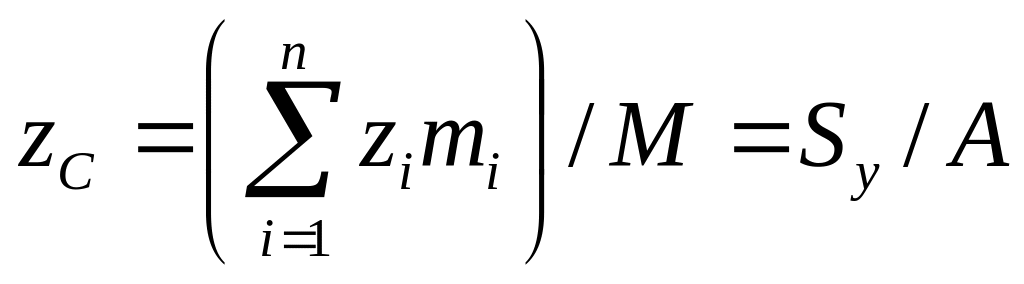
где — массы элементарных площадок сечения; М — масса сечения; А — площадь сечения; , —статические моменты сечения относи­тельно координатных осей OZ и OY соответственно.

Из приведенных выражений видно, что при =0, =0, т.е. при прохождении координатных осей через центр масс С, статические мо­менты сечения относительно этих осей будут равны нулю, так как . Такие координатные оси называют центральными. Это следст­вие можно выразить еще так: если статические моменты сечения от­носительно координатных осей, например OZ и OY, равны нулю, т.е. , , то эти оси проходят через центр масс С сечения.

4.3 Моменты инерции сечений

Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных пло­щадок и квадратов расстояний от них до данного полюса (точки). Из рис. 4.2 находим:

где — расстояние от площадки до полюса (точки О),

Рис. 4.2

Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных пло­щадок и квадратов расстояний от них до оси. Так, моменты инерции сечения относительно координатных осей OZ и OY Отбудут соответст­венно равны:

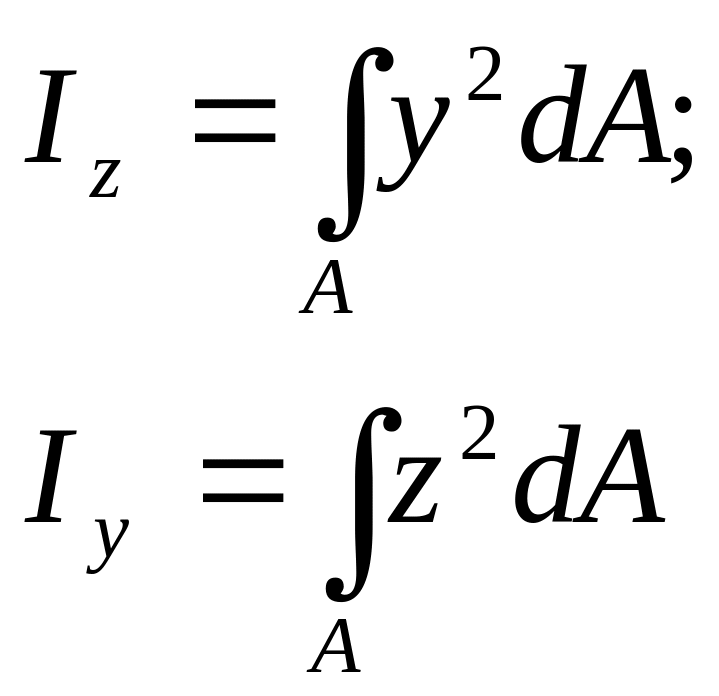
Так как , то, сравнив приведенные выражения, по­лучим

т.е. сумма осевых моментов инерции сечения относительно двух вза­имно перпендикулярных осей равна полярному моменту инерции это­го сечения относительно точки пересечения рассматриваемых осей. Моменты инерции сечений — всегда положительные величины.