34) Принцип суперпозиции состояний. Потенциальный барьер

Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.

Если функции   и   являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция,  , также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины   в состоянии   приводит к определённому результату  , а в состоянии   — к результату  , то измерение в состоянии   приведёт к результату   или   с вероятностями   и   соответственно.

Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.

Потенциа́льный барье́р — область пространства, разделяющая две другие области с различными или одинаковыми потенциальными энергиями. Характеризуется «высотой» — минимальной энергией классической частицы, необходимой для преодоления барьера.

На приведённом изображении участок BNC является потенциальным барьером для частицы с энергией E1. Потенциальным барьером для частицы с энергией E2 служит участок от нуля до точки D, так как частица не в состоянии подойти к началу координат ближе, чем координата точки D.

В классической механике, в случае, когда частица не обладает энергией, большей максимума для данного барьера, она не сможет преодолеть потенциальный барьер. В квантовой механике, напротив, возможно преодоление барьера с определённой вероятностью (туннельный эффект).

35)Тунельный эффект. Коэффициент прозрачности барьера.

Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера.

Краткое квантовомеханическое описание

Согласно классической механике, частица может находиться лишь в тех точках пространства, в которых её потенциальная энергия — Upot, меньше полной. Это следует из того обстоятельства, что кинетическая энергия частицы   не может (в классич. физике) быть отрицательной, так как в таком случае импульс будет мнимой величиной. То есть, если две области пространства разделены потенциальным барьером, таким, что  , просачивание частицы сквозь него в рамках классической теории оказывается невозможным. В квантовой же механике мнимое значение импульса частицы соответствует экспоненциальной зависимости волновой функции от её координаты. Это показывает уравнение Шрёдингерас постоянным потенциалом:

(упрощенное уравнение Шрёдингера в одномерном случае) где   координата;   полная энергия,   потенциальная энергия,   редуцированная постоянная Планка,   масса частицы).

Если  , то решением этого уравнения является функция:

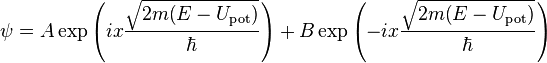
Пусть имеется движущаяся частица, на пути которой встречается потенциальный барьер высотой  , а потенциал частицы до и после барьера  . Пусть также начало барьера совпадает с началом координат, а его «ширина» равна  .

Для областей   (до прохождения),   (во время прохождения внутри потенциального барьера) и   (после прохождения барьера).получаются соответственно функции:

где  , 

Так как слагаемое   характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить  . Для характеристики величины туннельного эффекта вводится коэффициент прозрачности барьера, равный модулю отношения плотности потока прошедших частиц к плотности потока упавших:

Для определения потока частиц используется следующая формула:

где знак * обозначает комплексное сопряжение.

Подставляя в эту формулу волновые функции, указанные выше, получим

Теперь, воспользовавшись граничными условиями, выразим сначала   и   через   (с учетом, что  ):

а затем   через  :

Введем величину

которая будет порядка единицы. Тогда:

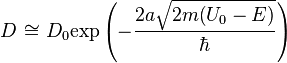
Для потенциального барьера произвольной формы делаем замену

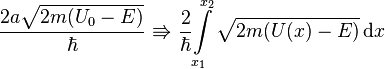
где   и   находятся из условия

Тогда для коэффициента прохождения через барьер получаем выражение