15.2. Сплайновые кривые

Будем использовать параметрические уравнения кривой. Параметрически заданной кривой называется множество γ точек М(х, у, z), координаты х, у, z которых определяются соотношениями:

,

которые называются параметрическими уравнениями кривой γ, где x(t), y(t), z(t) функции, непрерывные на заданном интервале a≤t≤b.

Если представить, что мы вводим новую переменную

,

то можно представить, что a=0, b=1, т. е. осуществить нормализацию параметров функции.

Часто используют векторную форму записи параметрических уравнений:

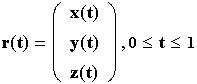
Параметр t задает ориентацию параметризованной кривой r(t) (порядок прохождения точек при монотонном возрастании параметра).

Дальше можно задавать первую производную кривой и если r'(t) = 0 в каждой точке, то кривая называется регулярной, т. е. в каждой точке кривой существует касательная.

Если дополнительно потребовать, чтобы задающая кривую векторная функция имела вторую производную, то будет определен вектор кривизны кривой

15.3. Сглаживающие кривые. Кривая Безье

Кривой Безье, определяемой массивом V (рис. 15.3.1), называется кривая, определяемая векторным уравнением:

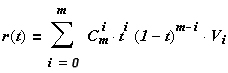t Є [0, 1],

где

биномиальный коэффициент, Cⁱ_m – число сочетаний из m элементов по i.

Кривая Безье обладает замечательными свойствами:

• она является гладкой;

• начинается в точке V₀ и заканчивается в точке V_m , касаясь при этом отрезков V₀ V₁, и V_m-1V_m контрольной ломаной;

• функциональные коэффициенты Cⁱ_mtⁱ(1-t)^m-i при вершинах V_i, i=0,I,....m, представляет собой универсальные многочлены (многочлены Бернштейна); они неотрицательны, и их сумма равна единицы:

Рис. 15.3.1. Кривая Безье, построенная по заданной последовательности массива точек V.

Поэтому кривая Безье целиком лежит в выпуклой оболочке, порождаемой массивом точек.

При m = 3 получаем (элементарную) кубическую кривую Безье, определяемую четверкой точек V₀, V₁, V₂, V₃ и описываемую векторным параметрическим уравнением:

t  [0, 1].

Порядок точек в заданном наборе влияет на вид кривой Безье.

Рис. 15.3.2. Примеры построения кривых Безье в зависимости от порядка задания вершин массива.

134