11.3. Закраска области, заданной цветом границы

Рассмотрим область, ограниченную набором пикселов заданного цвета, и точку (х, у), лежащую внутри этой области.

Задача заполнения области заданным цветом в случае, когда область не является выпуклой, может оказаться довольно сложной.

Простейший алгоритм, хотя и абсолютно корректно заполняющий даже самые сложные области, является слишком неэффективным, так как для всякого уже отрисованного пиксела функция вызывается еще 3 раза и, кроме того, этот алгоритм требует слишком большого стека из-за большой глубины рекурсии (рис 11.3.1).

Рис. 11.3.1. Алгоритм закраски 4-х соседних пикселей относительно заданного

    Поэтому для решения задачи закраски области предпочтительнее алгоритмы, способные обрабатывать сразу целые группы пикселов, т. е. использовать их "связность" - если данный пиксел принадлежит области, то скорее всего его ближайшие соседи также принадлежат данной области.     Ясно, что по заданной точке (х, у) отрезок [x_l, х_r] (x_left – координата левой границы, х_right – координата правой границы) максимальной длины, проходящий через эту точку и целиком содержащийся в области, построить несложно. После заполнения этого отрезка необходимо проверить точки, лежащие непосредственно над и под ним. Если при этом мы найдем незаполненные пикселы, принадлежащие данной области, то для их обработки рекурсивно вызывается функция.

Этот алгоритм способен работать с областями самой сложной формы (рис. 11.3.2).

Рис. 11.3.2. Закраска сложной области по линейкам пикселов

 

 

11. Закрашивание

0. Функция закрашивания

Световая энергия, падающая на поверхность от источника света, может быть поглощена, отражена и пропущена. Количество поглощенной, отраженной и пропущенной энергии зависит от длины световой волны. При этом цвет поверхности объекта определяется поглощаемыми длинами волн.

Свойства отраженного света зависят от формы и направления источника света, а также от ориентации освещаемой поверхности и ее свойств. Свет, отраженный от объекта, может быть диффузным и зеркальным: диффузно отраженный свет рассеивается равномерно по всем направлениям, зеркальное отражение происходит от внешней поверхности объекта.

Свет точечного источника отражается от идеального рассеивателя по закону косинусов Ламберта:

,

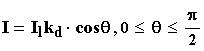где I интенсивность отраженного света;

I_l – интенсивность точечного источника;

k_d – коэффициент диффузного отражения (константа, 0 ≤ k ≤ l);

θ – угол между направлением на источник света и (внешней) нормалью к поверхности (рис. 12.1.1).

Рис. 12.1.1. Пример расположения единичных векторов нормали (вектор n) к освещаемой поверхности, вектора определяющего направление на источник (вектор l) и угла меду ними (угол θ)

    На объекты реальных сцен падает еще и рассеянный свет, соответствующий отражению света от других объектов. Поскольку точный расчет рассеянного освещения требует значительных вычислительных затрат, в компьютерной графике при вычислении интенсивности поступают так:

,

где I_a – интенсивность рассеянного света;

k_a – (постоянный) коэффициент диффузного отражения рассеянного света, 0 ≤ k_a ≤ 1.

Интенсивность света, естественно, зависит от расстояния d от объекта до источника света. Для того чтобы учесть это, пользуются следующей моделью освещения:

,

где k произвольная постоянная.

Интенсивность зеркально отраженного света зависит от угла падения, длины волны и свойств вещества. Так как физические свойства зеркального отражения довольно сложны, то в простых моделях освещения обычно пользуются следующей эмпирической моделью (моделью Фонга):

,

где k_s – экспериментальная постоянная;

α – угол между отраженным лучом и вектором наблюдения;

р – степень, аппроксимирующая пространственное распределение света. Объединяя последние две формулы, получаем модель (рис. 12.1.2) освещения (функцию закраски), используемую для расчета интенсивности (или тона) точек поверхности объекта (или пикселов изображения):

Рис. 12.1.2. Модель освещения

    Функцию закраски, используя единичные векторы внешней нормали n, а также единичные векторы, определяющие направления на источник (вектор l), отраженного луча (вектор r) и наблюдения (вектор s), можно записать в виде скалярных произведений:

.

    Замечание: Чтобы получить цветное изображение, необходимо найти функции закраски для каждого из трех основных цветов красного, зеленого и синего. Поскольку цвет зеркально отраженного света определяется цветом падающего, то постоянная k_s считается одинаковой для каждого из этих цветов.

Если точечных источников света несколько, скажем что модель освещения определяется так:

Если освещаемая поверхность в рассматриваемой точке гладкая (имеет касательную плоскость), то вектор внешней нормали вычисляется непосредственно. В случае многогранной поверхности векторы внешних нормалей можно найти только для ее граней. Что касается направлений векторов внешних нормалей на ребрах и в вершинах этой поверхности, то их значения можно найти только приближенно.

Пусть, например, грани, сходящиеся в данной вершине, лежат в плоскостях, описываемых уравнениями:

Можно считать, что нормальные векторы этих плоскостей (А_i,В_i,С_i) i=l,...,m, являются векторами внешних нормалей для рассматриваемой многогранной поверхности (если какой – то из нормальных векторов не является внешним, то достаточно поменять знаки его координат на противоположные). Складывая эти векторы, получаем вектор, определяющий направление приближенной нормали

Рис. 12.1.3. Представление граней примыкающих к ребру

Рис. 12.1.4. Многогранная поверхность заданная вершинами: V₁, V₂, V₃, V₄

Замечание. Для определения направления приближенной нормали в точке, лежащей на ребре многогранной поверхности, достаточно сложить векторы внешних нормалей, примыкающих к этому ребру граней рассматриваемой поверхности. Можно поступить и по - иному. А именно, аппроксимировать переменный вектор нормали вдоль ребра многогранной поверхности при помощи уже найденных векторов внешних нормалей в вершинах, прилегающих к рассматриваемому ребру.

Пусть многогранная поверхность задана своими вершинами. Тогда векторы, определяющие направления приближенных внешних нормалей в ее вершинах можно найти, используя векторные произведения, построенные на векторах, идущих вдоль ребер, исходящих из соответствующих вершин. Например, для того, чтобы определить внешнюю нормаль в вершине V₁, необходимо сложить векторные произведения.

Замечание. Если перед сложением найденные векторные произведения пронормировать, то полученная сумма будет отличаться от предыдущей и по длине, и по направлению.

Для отыскания направления вектора отражения напомним, что единичные векторы падающего света l, нормали к поверхности n и отражения лежат в одной плоскости, причем угол падения равен углу отражения.

Рассмотрим модель освещения с одним точечным источником и предположим, что свет падает вдоль оси Z. Тогда координаты единичного вектора отражения

определяются по формулам

где – единичный вектор нормали к поверхности.

Если же свет от источника, падает не по оси аппликат, то проще всего поступить так: выбрать новую координатную систему так, чтобы ее начало совпадало с рассматриваемой точкой, касательная плоскость к поверхности была плоскостью ху, а нормаль к поверхности в этой точке шла вдоль оси Z. В этой новой системе координаты векторов r и l будут связаны соотношениями:

.

Для того чтобы получить исходные координаты вектора отражения, необходимо выполнить обратное преобразование.

Рассмотрим произвольную сцену, составленную из полигональных (многогранных) фигур. Простейший способ ее построения заключается в том, что на каждой из граней выбирается по точке, для нее определяется освещенность, и затем вся грань закрашивается с использованием найденной освещенности. Предложенный алгоритм обладает, однако, одним большим недостатком полученное изображение имеет неестественный многогранный вид. Это объясняется тем, что определяемая подобным образом освещенность сцены не является непрерывной величиной, а имеет кусочно-постоянный характер.

Существуют специальные методы закрашивания, позволяющие создавать иллюзию гладкости.

Опишем два известных метода построения сглаженных изображений.