7.2. Векторная графика

    Изображение, созданное в векторных программах, основывается на математических формулах, а не на координатах пикселей и информации об их цвете. Поэтому векторные файлы содержат наборы инструкций для построения геометрических объектов – линий, эллипсов, прямоугольников, многоугольников и дуг. В соответствии с этим основу векторных изображений составляют разнообразные линии и кривые, называемые векторными, или, по-другому, контурами. Каждый контур представляет собой независимый объект, который можно редактировать: перемещать, изменять, масштабировать. При этом качество изображения не изменяется (рис.2.2.1.), так как после внесения каких-либо изменений в файл происходит пересчет размера и места положения объекта изображения (т.е. при каждом выводе изображения происходит новый расчет изображения по математическим формулам, следовательно, образование «ступенек», как в растровой графике, невозможно).

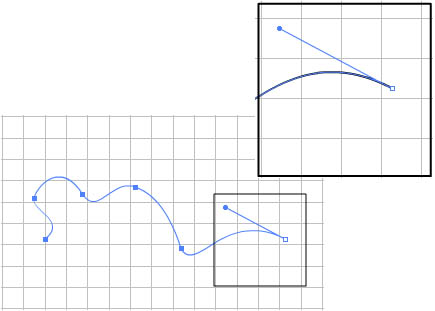
Рис. 7.2.1 Пример изменения масштаба векторного изображения

    Достоинствами являются экономия памяти четкость изображения, недостатками – невозможность автоматического ввода.

Векторные изображения могут быть созданы с помощью нескольких видов программ.

    Это, в частности:

программы векторной графики;

программы САПР, типичным представителем которых является программа AutoCAD; специальные программы конвертирования растровых изображений в векторные. Одна из таких программ – CorelTrace9, входящая в состав графического редактора CorelDraw.

0. Фрактальная графика

Понятие фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур. Объект называется самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Определение фрактала, данное Мандельбротом: фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.

К фрактальным множествам относят множество Кантора и ковер Серпинского. Они обладают геометрической инвариантностью и называются «множествами средних третей». Простейший вариант множества Кантора строится следующим образом.

Рис. 7.3.1. Построение множества Кантора

Рассмотрим отрезок единичной длины на вещественной оси. Этот отрезок делится на три равные части, причем средняя часть вырезается (рис.7.3.1). Далее с каждым из оставшихся отрезков происходит то же самое: они делятся на три равные части, и средние части удаляются. В результате получается последовательность отрезков убывающей длины. На первом этапе это один отрезок, на втором – два, на третьем – четыре и т.д., на k–м – 2k. При k®¥ получим множество точек, называемое множеством Кантора. Суммарная длина всех вырезанных отрезков равна 1.

Множество Кантора является фракталом. Для фрактала введено понятие фрактальной размерности. Для множества Кантора, которое состоит из N = 2n, разделенных интервалов длиной ε = (1/3)n, фрактальная размерность равна:

ФР = n ln2/n ln3 ≈ 0,63

Обобщение множества Кантора средних третей на случай плоских фигур приводит к ковру Серпинского. Например, возьмем квадратную матрицу и разделим ее на девять равных квадратов. При первой итерации удалим центральный квадрат, аналогично поступим с каждым из оставшихся восьми квадратов и т.д. Пересечение полученных при k®¥ множеств – это ковер Серпинского (рис. 7.3.2). Для ковра Серпинского фрактальная размерность равна ФР »1,893.

Рис.7.3.2. Построение ковра Серпинского

а) б)

Рис 7.3.3. Примеры 2-х мерных фрактальных изображений: а) «Клоп», б) «Лиана»

Рис. 7.3.4. Примеры 3-х мерных фракталов: а) Коха, б) «Куб»