Описание испытательной установки

Испытательная установка для исследования косого изгиба (рис. 6.5) представляет собой стальной стержень с прямоугольным поперечным сечением (размеры сечения b, h), один конец которого защемлен. Нагрузка F на стержень создается весом грузов. Линия действия силы F составляет угол α с осью y, являющейся главной центральной осью инерции сечения. На расстоянии L от линии действия силы F на ребрах стержня наклеены два тензорезистора, позволяющие определить деформации в точках A, B.

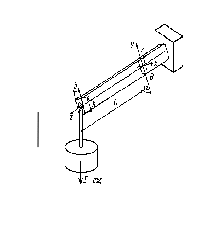
Рис. 6.5. Схема установки для исследования косого изгиба

Описание принципа действия тензорезисторов, их конструкции, схемы подключения к измерительной цепи и методики тарировки тензометрической установки перед проведением измерений приведены в лабораторной работе 5.

Порядок проведения работы

1. Включить монитор, крейтовую систему сбора данных и управляющую ПЭВМ, а после загрузки последней запустить управляющую программу, если она не запустилась автоматически. После прогрева тензоусилителей, входящих в состав крейта, в течение не менее чем 5 минут можно приступать к измерениям.

2. Ознакомиться с испытательной установкой, образцом и тензоизмерительной аппаратурой. Внести в отчет: размеры поперечного сечения образца b и h; расстояние от места приложения силы до точек, в которых определяется напряжение, L; угол поворота балки α; модуль продольной упругости Е материала образца (см. лаб. работу №5, табл. 5.1)

3. Сбросить показания прибора на ноль.

4. Аккуратно поместить груз (масса груза задается преподавателем) на подвеску и записать значения относительной линейной деформации под каждым из двух тензорезисторов (в точках сечения А и В).

5. Снять груз, при необходимости установить показания прибора на ноль и повторить опыт еще 2 раза. Если грузы будут совершать колебания, то ввиду высокой чувствительности прибора показания его будут непрерывно меняться, поэтому перед установкой прибора на ноль и перед снятием показаний подвеску с грузами необходимо успокоить вручную.

6. По окончании работы необходимо снять грузы с подвески. Если ПЭВМ в дальнейшем не требуется для проведения измерений или выполнения расчетов, то ее, крейт и монитор необходимо выключить.

7. Вычислить средние значения деформаций  по трем опытам под каждым тензорезистором.

8. Используя закон Гука для линейного напряженного состояния, определить экспериментальные значения напряжений для каждой точки сечения:

.

(6.2)

9. Вычислить по формуле (6.1) напряжения σ_теор в соответствующих точках сечения.

10. Определить значение относительной погрешности:

.

(6.3)

11. Результаты измерений и расчетов занести в таблицу 6.1.

Таблица 6.1.

Точка сечения	Показания прибора			Средняя экспериментальная относительная линейная деформация 	Экспериментальное напряжение σэксп, МПа	Теорети-ческое напряжение σтеор, МПа	Относительная погрешность, %
	опыт 1	опыт 2	опыт 3
A
B

12. Сделать вывод о точности и применимости положений и допущений, используемых в аналитическом расчете сложного напряженного состояния материала при косом изгибе.

13. Построить расчетные схемы, эпюры поперечных сил и изгибающих моментов для балки с учетом истинных значений угла  и силы F. Найти значения изгибающих моментов в исследуемом сечении

Описанная выше экспериментальная установка может быть использована для определения нормальных напряжений при плоском прямом изгибе. В этом случае плоскость действия внешних сил совпадает с одной из главных осей сечения, т.е. угол  = 0. При проведении экспериментов для этого случая стержень поворачивается вокруг продольной оси до тех пор пока линия действия силы F (cм. рис. 6.5) не совпадет с осью y и угол  не становится равным нулю. В этом положении стержень фиксируется в заделке. Далее эксперимент и обработка его результатов проводится по той же методике, что и для косого изгиба, с учетом того что в уравнении (6.1) одно из напряжений равно нулю.