9. Термодинамическая вероятность макросостояния (статистический вес)

            Рассмотрим простую модель системы, состоящей всего из двух подсистем (ячеек), в которых находятся четыре частицы с номерами от 1 до 4. Ячейки соответствуют либо двум разным координатам частиц (расположению частиц в двух разных местах), либо два разным импульсам частиц (смотри таблицу).

Способ распределения частиц по ячейкам без учета их номеров называется макросостоянием системы.

В рассматриваемом примере возможны всего пять разных макросостояний (три из них схематически изображены в таблице). 1 – все четыре частицы находятся в левой ячейке, 2 – три частицы в левой ячейке и одна в правой, 3 – две частицы в левой ячейке и две в правой. Ещё два макросостояния симметричны первому и второму.

 

Возможные макро и микросостояния для модели   системы, состоящей из двух ячеек с четырьмя частицами

Способ распределения частиц по ячейкам с учетом их номеров называется микросостоянием системы. Возможные микросостояния представлены в третьей колонке таблицы. Вероятность застать систему невзаимодействующих частиц в любом из перечисленных микросостояний одна и та же. Но число микросостояний, реализующих макросостояние 3, максимальное, и это макросостояние возникает чаще других. Оно является предпочтительным для системы.

Число микросостояний, соответствующих какому-либо макросостоянию системы, называется термодинамической вероятностью (статистическим весом) этого макросостояния. Термодинамическую вероятность будем обозначать буквой W. В последнем столбце приведены значения термодинамической вероятности для первых трех макросостояний. В простом рассматриваемом примере эти числа невелики, тогда как термодинамическая вероятность макросостояний систем, состоящих из большого числа частиц (порядка числа Авогадро), выражается, соответственно, числами очень высоких порядков.

                Рассмотрим свойства термодинамической вероятности. 

1). Равновесие и флуктуации. Если на термодинамическую систему нет внешних воздействий, то в результате теплового движения частиц она случайно оказывается то в одном, то в другом макросостоянии. Но чаще всего осуществляются состояния с высокой термодинамической вероятностью. Равновесному состоянию соответствует максимальная термодинамическая вероятность. Состояния, очень близкие к равновесному, также имеют высокие термодинамические вероятности, и система случайным образом осуществляет переходы между ними вблизи равновесия. Используют термин: термодинамическая вероятность флуктуирует вблизи максимального значения. При этом флуктуируют и некоторые параметры состояния. Например для газа в маленьких локальных областях наблюдаются малые флуктуации давления вблизи равновесного его значения. Также флуктуационным является воздействие молекул жидкости на броуновскую частицу.

                Главное свойство термодинамической вероятности: W® max в самопроизвольных процессах.

2). Термодинамическая вероятность – характеристика состояния. Термодинамическая вероятность любого макросостояния системы не зависит от предшествующих и будущих состояний. Изменение термодинамической вероятности при переходе от одного макросостояния к другому не зависит от пути перехода, а зависит только от начального и конечного макросостояний. При циклическом процессе термодинамическая вероятность возвращается к исходному значению.

3). Мультипликативность. Если сложная система состоит из отдельных невзаимодействующих подсистем, то термодинамическая вероятность состояния сложной системы равна произведению термодинамических вероятностей состояний подсистем: .

Последнее свойство не является “удобным”. Физика стремится вводить в рассмотрение не мультипликативные, а аддитивные величины, то есть такие, которые складываются друг с другом (как масса, энергия и др.), а не перемножаются, как термодинамические вероятности. Переход к аддитивным величинам не всегда возможен, но в данном случае придумана очень удобная величина со свойством аддитивности – энтропия.

 Свойства энтропии

Энтропия дискретного источника всегда положительна. Это определяется способом ее подсчета.

,

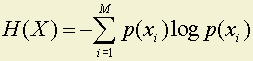где 0 ≤ p(x_i) ≤ 1 – положительное число;

0 ≤ [–log p(x_i)] ≤ ∞ – положительное число;

0 ≤ –p(x_i)log p(x_i) ≤ 0.531 – положительное число;

H(x) – сумма положительных чисел.

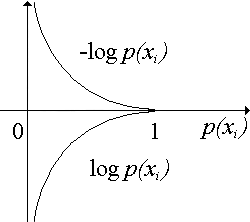Рис. 2.2

Энтропия равна нулю только в том случае, когда вероятность появления одной из букв источника равна 1, а всех остальных – нулю.

2. Можно доказать, что максимум энтропии достигается при равных вероятностях появления букв алфавита, то есть

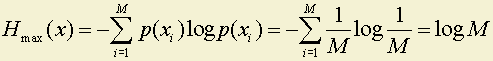
Покажем это на примере источника из двух букв.

H(x) = –plog p – qlog q = –plog p – (1 – p)log(1 – p),

где H(x), будет максимально, когда H '(x), то есть

,

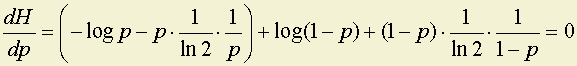откуда следует, что –log p + log(1 – p) = 0; и p = 0.5 = q.

Максимум H(x) равен в данном случае 1 или H_max(x) = log M.

3. Если в системе событие x_k состоит из двух событий x'_k и x"_k с вероятностями q₁ и q₂ (q₁ + q₂ = p_k), то общая энтропия системы будет равна сумме энтропий исходной системы и энтропии разветвленной части с весом p_k и условными вероятностями ветвления ^q₁⁄_pk и ^q₂ ⁄_pk , то есть H{x₁; x₂; ... x_k-1; x'_k; x"_k} = H{x₁; x₂; ... x_k-1; x_k} + p_kH(x'_k; x"_k).

Покажем это на примере.

Пусть имеется система с двумя состояниями.

H(x₁; x₂) = (–0.5log 0.5) · 2 = 1 бит.

Пусть состояние x₂ разбилось на два.

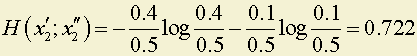 бита.

Энтропию новой системы можно подсчитать двумя способами:

1.

H_сист = –0.5log 0.5 – 0.4log 0.4 – 0.1log 0.1 = 0.5 + 0.529 + 0.332 = 1.361 бита.

2. H_сист = H(x₁; x₂) + p(x₂) · H(x'₁; x"₂) = 1 + 0.5 · 0.722 = 1.361 бита.

Как видим, ответ получился один и тот же, но при втором способе расчета не нужно пересчитывать всю систему, а только к старой энтропии добавить энтропию разветвления.

Рассмотрим примеры на расчет энтропии по Шеннону и сравним ее с информацией по Хартли.