На діагоналі коваріаційної матриці отримуємо дисперсії коефіцієнтів регресіїbj:

D(b₀) = 318,9421,

D(b₁)=0,002358,

D(b₂)=272,2121,

D(b₃)=0,007489

Визначимо значення стандартних помилок коефіцієнтів регресіїSbj:

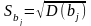
S_b0 = = 17,85895,

S_b1 = = 0,048839,

S_b2 =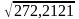 = 16,49885,

S_b3 = = 0,086537

17,85895

0,048839

16,49885

0,086537

S_b =

Розрахункове значення t-статистики отримуємо для кожного коефіцієнта:

t_b0 = b₀ / S_b0 = -23,83/ 17,85895 = -1,33433 і т. п.

-1,33433

4,658181

0,546609

1,121298

t_p =

Розрахункові значення t-статистики порівнюються за абсолютною величиною з табличним t_10-4 = 1,943. Параметр вважається статистично значимим (нульова гіпотеза не підтверджується), якщо

Це означає, що в нашому випадку тільки b₁є статистично значущим і суттєво впливає на модель.

Довірчі інтервали для оцінок регресії будуються за формулою:

b0 =-23,829834,699

b1 =0,22750,0949

b2 =9,01842332,0573

b3 =0,0970340,1681

:

19. а) Обчислимо F-статистику за формулою

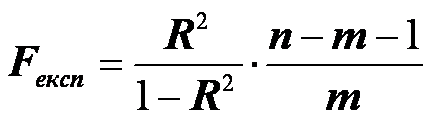
Знайти табличне значення: і порівняти його з обчисленою F – статистикою: якщо то гіпотеза відхиляється, інакше приймається.  

            Маємо Fексп=39,14827, табличне значення:

Порівняємо його з обчисленою F-статистикою. Оскільки нульова гіпотеза відхиляється, тобто коефіцієнти регресії є значущими.  

20. . Прогнозування за багатофакторною регресійною моделлю.

Прогнозування на основі регресійних моделей передбачає такі етапи:

Визначення мети дослідження. Вибір відповідної теорії, яка пояснює поведінку економічної системи. Побудова системи показників, відбір чинників, що справляють найбільший вплив на кожен показник, та розроблення логіко-інформаційної схеми прогнозу. Вибір форми зв’язку показників між собою та відібраними чинниками.

Побудова економетричної моделі, тобто відображення теорії у вигляді рівняння регресії або системи рівнянь і тотожностей, яка пов’язує відібрані змінні. Особливо слід зважати на випередження та запізнення впливу змінних у рівняннях, а також на змінні, що містять інформацію про перспективу на майбутнє.

Знаходження даних про значення змінних, дотримуючись, за можливості, теоретичних концепцій. Аналіз інформації. В ідеалі потрібні точні дані про всі необхідні змінні.

Використання відповідного економетричного методу для оцінювання невідомих параметрів, які входять до рівнянь моделі.

Перевірка якості побудованої моделі, яка передбачає, передусім, її відповідність досліджуваному економічному процесу, а також адекватність, точність і прогнозову спроможність.

Використання знайденої прийнятної моделі для прогнозу. На підставі рівнянь із оціненими параметрами та прогнозованих екзогенних змінних роблять передбачення потрібних показників, а саме значень ендогенних змінних. Якщо потрібен прогноз на кілька періодів уперед, його можна одержати шляхом послідовності прогнозів на один період. Знайти значення величин екзогенних змінних, від яких суттєво залежить прогноз, можна або на основі одновимірної моделі часових рядів, або використовуючи інші джерела, наприклад іншу економетричну модель або експертні методи.

21. рогнозне значення   визначається за шляхом підстановки у рівняння регресії (4) відповідних значень факторів  :

.       (14)

Довірчий інтервал прогнозу обчислюється за слідуючими формулами:

,       (15)

де        - умовне математичне сподівання залежної змінної в точці прогнозу;

 - оцінка стандартної похибки прогнозу, яка обчислюється за формулою  

;       (16)

            - матриця значень факторів;

            - вектор (матриця-стовпець) значень факторів для прогнозу.

 

          Довірчі інтервали для коефіцієнтів регресійної моделі:

,  .       (17)

22. . Визначення мультеколініарності та її природа. Практичні наслідки мультиколініарності.

1. Поняття про мультиколінеарність та її вплив на оцінку параметрів моделі Означення: Суть мультиколінеарності полягає в тому, що в багатофакторній регресійній моделі дві або більше незалежних змінних пов'язані між собою лінійною залежністю або, іншими словами, мають високий ступінь кореляції:                                                                                             23. Наслідки мультиколінеарності

                            Практичні наслідки мультиколінеарності: Мультиколінеарність незалежних змінних (факторів) призводить до:

•  зміщення оцінок параметрів моделі, які розраховуються за методом найменших квадратів.

• збільшення дисперсії та коваріації оцінок параметрів, обчислених за методом найменших квадратів

•  збільшення довірчого інтервалу (оскільки збільшується середній квадрат відхилення параметрів)

• незначущість t-статистик:                                                    

Зауваження.   Мультиколінеарність не є проблемою, якщо єдиною метою регресійного аналізу є прогноз (оскільки чим більше значення R2, тим точніший прогноз). Якщо метою аналізу є не прогноз, а дійсне значення параметрів, то мультиколінеарність перетворюється на проблему, оскільки її наявність призводить до значних стандартних похибок оцінок параметрів.  

24. ТестАлгоритм Фаррара-Глоубера.

Тестування наявності мультиколінеарності.

Зовнішні ознаки наявності мультиколінеарності

• Велике значення R2 і незначущість t-статистики

•  Велике значення парних коефіцієнтів кореляції.

Для визначення мультиколінеарності здебільшого застосовують такі тести: - F-тест, запропонований Глобером і Фарраром ( інша назва: побудова допоміжної регресії) - Характеристичні значення та умовний індекс  

                                                            Алгоритм Фаррара-Глобера: 1. Визначити критерій Пірсона χ2 (“хі”- квадрат),  для цього знайти: а). нормалізовані змінні х1, х2, …, х m:                                                                    

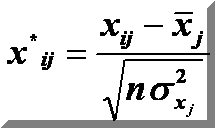
б).на основі матриці нормалізованих змінних, обчислити кореляційну матрицю:                                                            

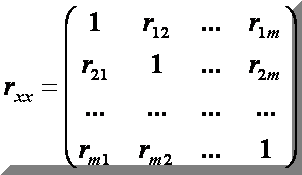
в).обчислити визначник кореляційної матриці: г). обчислити критерій χ2:

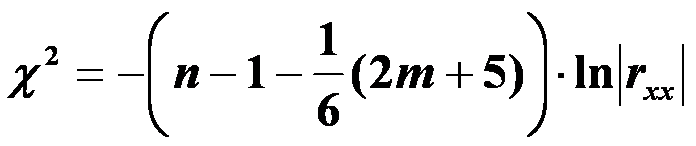
Порівняти значення χ2 з табличним при 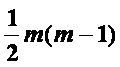   ступенями свободи і рівні значущості α,(якщо χ2> χ2табл, то в масиві незалежних змінних існує мультиколінеарність).  

2. Обчислити F- критерій Фішера. а).обчислити матрицю похибок:

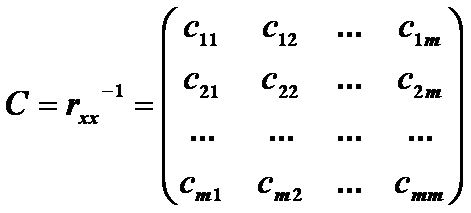
б).розрахувати F- критерії

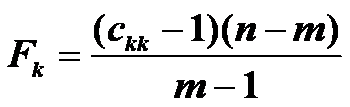
 Порівняти значення Fk з табличним при ступенями свободи і рівні значущості α (якщо Fk>Fтабл, то відповідна k-та незалежна змінна мультиколінеарна з іншими). в). розрахувати коефіцієнти детермінації для кожної змінної:

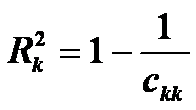
3. Визначити t- критерій Ст’юдента:  

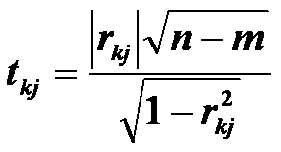              де                    

Порівняти значення              з табличним при                  

ступенями свободи і рівні значущості α (якщо то між незалежними змінними хk та хj існує мультиколінеарність). F-тест Нехай - коефіцієнт детермінації в регресії, яка пов'язує фактор хi з іншими факторами. 1) для кожного коефіцієнта детермінації розраховуємо Fi-відношення:

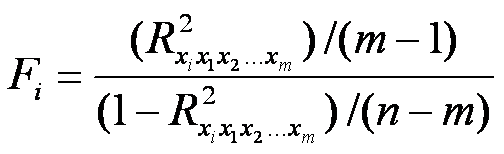
F-тест перевіряє гіпотезу Н0 : проти гіпотези Н1: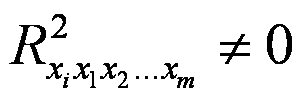

2) Fкр знаходимо за таблицею F-розподілу Фішера з (т-1) і (п-т) ступенями свободи і заданим рівнем значущості; 3) якщо Fi > Fкр , то гіпотезу Н0 відкидаємо (хi — мультиколінеарний фактор), якщо Fi< Fкр , то гіпотезу Но приймаємо (фактор хi не є мультиколінеарним).

25.Тест Фаррара-Глоубера

26. Для визначення мультиколінеарності здебільшого застосовують такі тести: - F-тест, запропонований Глобером і Фарраром ( інша назва: побудова допоміжної регресії) - Характеристичні значення та умовний індекс  

                                                            Алгоритм Фаррара-Глобера: 1. Визначити критерій Пірсона χ2 (“хі”- квадрат),  для цього знайти: а). нормалізовані змінні х1, х2, …, х m:                                                                    

б).на основі матриці нормалізованих змінних, обчислити кореляційну матрицю:                                                            

в).обчислити визначник кореляційної матриці: г). обчислити критерій χ2:

Порівняти значення χ2 з табличним при    ступенями свободи і рівні значущості α,(якщо χ2> χ2табл, то в масиві незалежних змінних існує мультиколінеарність).  

2. Обчислити F- критерій Фішера. а).обчислити матрицю похибок:

б).розрахувати F- критерії

 Порівняти значення Fk з табличним при ступенями свободи і рівні значущості α (якщо Fk>Fтабл, то відповідна k-та незалежна змінна мультиколінеарна з іншими). в). розрахувати коефіцієнти детермінації для кожної змінної:

3. Визначити t- критерій Ст’юдента:  

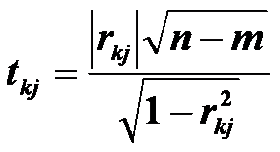              де                    

Порівняти значення              з табличним при                  

ступенями свободи і рівні значущості α (якщо то між незалежними змінними хk та хj існує мультиколінеарність). F-тест Нехай - коефіцієнт детермінації в регресії, яка пов'язує фактор хi з іншими факторами. 1) для кожного коефіцієнта детермінації розраховуємо Fi-відношення:

F-тест перевіряє гіпотезу Н0 : проти гіпотези Н1:

2) Fкр знаходимо за таблицею F-розподілу Фішера з (т-1) і (п-т) ступенями свободи і заданим рівнем значущості; 3) якщо Fi > Fкр , то гіпотезу Н0 відкидаємо (хi — мультиколінеарний фактор), якщо Fi< Fкр , то гіпотезу Но приймаємо (фактор хi не є мультиколінеарним).

27. Поняттягомо та гетероскидастичності.

Виявлення гетероскедастичності та її природа

Розглянемо класичну лінійну багатофакторну модель

Означення. Якщо дисперсія залишків стала для кожного спостереження, то це явище називається гомоскедастичністю:    

Якщо це припущення не задовольняється в якомусь окремому випадку, то маємо гетероскедастичність (помилки ui некорельовані, але мають несталу дисперсію). Означення. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, то це явище називається гетероскедастичністю:

Сутність припущення про гомоскедастичність полягає втому, що варіація кожної випадкової складової ui навколо її математичного сподівання не залежить від значення факторів х:

Форма гетероскедастичності залежить від знаків і значень коефіцієнтів у залежності

Оскільки ui — не спостережувана випадкова величина, ми не знаємо справжньої форми гетероскедастичності. В разі простої лінійної регресії гетероскедастичність має форму                                                               (k—const, яку потрібно оцінити)  Наслідки порушення припущення про гомоскедастичність: - Неможливо знайти середньоквадратичне відхилення параметрів - Неможливо побудувати довірчий інтервал для прогнозних значень упр  

Отримані за МНК оцінки параметрів регресії не є ефективними (не мають найменшої дисперсії)

28. Економетрична модель, якій притаманна гетероскедастичність є узагальненою моделлю, і для оцінювання її параметрів використовується так званий узагальнений метод найменших квадратів (УМНК) , або метод Ейткена. Свою назву метод отримав внаслідок його застосування для оцінювання параметрів моделі, для якої дисперсійно-коваріаційна матриця стохастичної складової моделі приймається у найбільш загальному вигляді ( 3 ), тобто допускається одночасно і гетероскедастичність і автокореляція залишків.

В основу методу Ейткена покладено ідею трансформації економетричної моделі, якій притаманна гетероскедастичність у класичну гомоскедастичну с подальшим застосуванням до такої трансформованої моделі процедури 1 МНК для оцінювання параметрів узагальненої моделі, якій притаманна гетероскедастичність. Трансформація вихідної моделі у гомоскедастичну відбувається шляхом корегування вихідної статистичної інформації стосовно змінних моделі. Спосіб і форма корегування вихідних даних визначаються, при цьому , формою залежності дисперсії стохастичної складової від тієї чи іншої пояснюючої змінної моделі.

Розглянемо більш докладно цей метод. Нехай є економетрична модель

, ( 10 )

для якої , де - як і раніше, деяка невідома константа , S – відома квадратна додатньо визначена матриця розмірністю nn, яка у випадку гетероскедастичності ,як показано раніше, є діагональною матрицею і має наступний вигляд :

, ( 11 )

де - власні значення цієї матриці.

Оскільки матриця S симетрична і додатньо визначена, то використовуючи теорію матриць її можна подати у наступному вигляді:

, ( 12 )

де матриця P є не виродженою і має вигляд

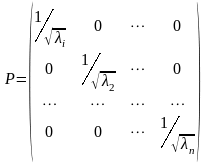, ( 13 )

а обернена до неї відповідно :

. ( 14 )

Базуючись на особливостях матриць SiPзапишемо деякі співвідношення між ними і оберненими до них :

( 15 )

і . ( 16 )

Помноживши рівняння ( 10 ) на матрицю P^-1, дістанемо :

( 17 )

Введемо наступні позначення : .

Тоді модель матиме вигляд:

. ( 18 )

Використовуючи ( 16 ) можна показати, що для цієї перетвореної моделі гетероскедастичність відсутня, оскільки

,

що дає змогу застосувати до трансформаційної моделі (18) 1МНК . Тоді отримаємо :

,

або з врахуванням ( 16 ) остаточно

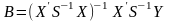. ( 19 )

Таким чином, якщо матриця S відома, за формулою ( 19 ) можна завжди обчислити оцінки параметрів моделі у разі гетероскедастичності. Проблема полягає у визначені власних Оскільки дійсні значення випадкової величини  _,як правило невідомі, значення _і у матриці Sможна обчислити користуючись різними гіпотезами відносно зв’язку дисперсії і деякої пояснюючої змінної х_j. В основному при цьому використовуються наступні 2 гіпотези.

Гіпотеза 1. Дисперсія залишків пропорційна до зміни пояснюючої змінної х_{j -} . Тоді величини _і визначається як:

. ( 20 )

Гіпотеза 2. Дисперсія залишків пропорційна до зміни квадрату пояснюючої змінної х_j - . Величини _і визначається для цієї гіпотези як:

. ( 21 )

29. На першому етапі на основі статистичної вибірки і припущень про відсутність гетероскедастичності будується класична економетрична модель і обчислюються залишки .

На другому етапі виконуються дослідження квадратів залишків і робиться висновок про наявність або відсутність гетероскедастичності. Для цього будуються графіки різних типів. Для парної лінійної моделі будується графік . Для моделі багатофакторної лінійної регресії найбільш розповсюдженими є графіки залежності або графіки , де x_j – пояснююча змінна, яка гіпотетично може впливати на дисперсію залишків. Якщо неможливо однозначно визначитися з такою змінною графіки будуються для всіх пояснюючих змінних моделі. Метою побудови таких графіків є встановлення наявності або відсутності систематичності у зміні квадратів залишків e² при зміні значення залежної змінної моделі y , або пояснюючої змінної x_j. Звичайно - це тільки оцінки невідомих , але вони можуть успішно використовуватися, особливо при великих вибірках.

Досліджуючи можна отримати наступні види графіків, які наведені на рис. 3.

Рис. 3. Типи графіків квадратів залишків

На рис. 3,а всі квадрати залишків знаходяться всередині шару постійної ширини, яка паралельна осі абсцис. Це свідчить про незалежність від залежної змінної y або пояснюючої змінної x_jі їх сталості, тобто у цьому випадку виконуються умови гомоскедастичності.

На рис. 3,б – г спостерігаються систематичні зміни у співвідношенні між значеннями y( або x_j ) і квадратами залишків . На рис. 3,б і 3,в відображена лінійна, а на рис.3,г – квадратична залежності між квадратами залишків і значеннями залежної або пояснюючої змінної моделі. Таким чином, ситуації , представлені на 3,б – г, свідчать про наявність у цих випадках гетероскедастичності.

Зауваження 2.Графічний метод дає можливість не тільки виявити гетероскедастичність, але й зробити висновок щодо самої форми зв’язку між дисперсією залишків і пояснюючими змінними моделі, що особливо важливо для побудови моделі при наявності гетероскедастичності.

30. Тестування наявності гетероскедастичності. Параметричний тест Гольфельдта-Квандта.