
- •1. Визначення предмета "Економетрія". Становлення економетрії та її звязок з математико-статистичними методами. Будова економтерії .
- •3. Етапи проведення економетричного аналізу. Розробка моделі .
- •4. Загальний вигляд простої вибіркової лінійної регресії .
- •5. Суть мнк.
- •6. Коефіціент кореляції, його властивості, перевірка гіпотези про значущість коефіціента кореляції .
- •8. Основні припущення
- •9. Перевірка простої регресійної моделі на адекватність за f-критерый Фішера,
- •15. Суть коефіцієнта детермінації
- •На діагоналі коваріаційної матриці отримуємо дисперсії коефіцієнтів регресіїbj:
- •Визначимо значення стандартних помилок коефіцієнтів регресіїSbj:
- •Алгоритм для параметричного тесту Гольдфельда-Квандта
- •33. Природа автокореляції. Основні поняття та означення.
- •37. 8.3.1. Метод Ейткена
- •А) прискорене зростання
- •В) спад
- •Б) уповільнене зростання
- •2.2. Показникова (експоненційна ) модель
- •2.3. Зворотна модель
- •2.4. Квадратичні моделі
15. Суть коефіцієнта детермінації
Коефіцієнт детермінації (R2)показує частку зміни (варіації) результативної ознаки під дією факторної ознаки. Розраховується за формулою:
Він може варіювати від 0 до 1. Чим ближче він до 1, тим адекватніше встановлена тенденція, і, відповідно, тіснішим є зв'язок вибраного тренду та динамічного ряду. Виходячи з величини коефіцієнта детермінації, в статистичній практиці прийнято застосовувати таку градацію відповідності тренду динамічному ряду: 0 - відсутність зв'язку; до 0,3 - слабка; від 0,3 до 0,6 - середня; від 0,7 до 0,9 - висока; від 0,9 до 1. - вибраний тренд повністю відповідає динамічному ряду. Потрібно також врахувати, що в Excel значення R2He є повністю коректним, але для цілей визначення адекватності вибраної функції цим можна знехтувати.
Отже коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції. Тому коефіцієнт кореляції може розраховуватись за формулою:
, або ,
де σy2 – загальна дисперсія ознаки y, ,
σyx2 – середній квадрат відхилення фактичних значень ознаки y від теоретичних значень yx, .
16. Коефіцієнт детермінації характеризує частку варіації результативної ознаки у, яка пов'язана з варіацією фактору х. За відсутності зв'язку R2=0. Якщо зв'язок функціональний, R2=1.
Скоригований коефіцієнт множинної детермінації відрізняється від R2 співвідношенням числа ступенів вільності дисперсій: залишкової (n – m + 1) і загальної (n – 1).
17. Коефіцієнт детермінації характеризує частку варіації результативної ознаки у, яка пов'язана з варіацією фактору х. За відсутності зв'язку R2=0. Якщо зв'язок функціональний, R2=1.
Корінь квадратний із коефіцієнта детермінації називають коефіцієнтом кореляції. Якщо зв'язок лінійний, то R =|r|. Перевірка істотності кореляційного зв'язку ґрунтується на порівнянні фактичних значень R2 з критичними, які могли б виникнути за відсутності зв'язку. Якщо фактичне значення R2 перевищує критичне, то зв'язок між ознаками не випадковий. Гіпотеза, що перевіряється, формулюється як нульова: Н0 : R2 = 0 .
Критичні значення характеристик щільності зв'язку для рівня істотності а = 0,05 і відповідного числа ступенів свободи наведено в табл. 4.4.2. Число ступенів свободи df залежить від обсягу сукупності n і кількості параметрів рівняння т.Для факторної дисперсії df дорівнює (т - 1), для залишкової - (п - т).
Розглянута процедура перевірки істотності зв'язку є складовою дисперсійного аналізу (див. 4.3). або .
Критичні значення , де α — рівень істотності, k1 = m – 1, k2 = n – (m – 1) — числа ступенів вільності чисельника та знаменника, наведено в додатку 10. Оскільки F-критерій функціонально зв’язаний з коефіцієнтом детермінації R2, то перевірку істотності зв’язку можна здійснити, використовуючи безпосередньо критичні значення . Критичні значення коефіцієнта детермінації R2для α =0,05
18. Дисперсійно-коваріаційна матриця параметрів багатофакторної регресії. Оцінка дисперсії стохастичної складової моделі .
дисперсійно-коваріаційну матрицю (іноді її називають коваріаційною).
Розраховується вона за формулою
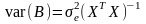 ,
,
де
 -
дисперсія залишків
-
дисперсія залишків
Матрицю С= ми маємо.
ми маємо.
 ,
де
,
де
n – кількість спостережень, n=10
m – кількість оцінюваних параметрів моделі, m=4.
Стандартне
відхилення залишків
 =
4,912352.
=
4,912352.
Отримуємо:
 =
=

