8. Основні припущення

Застосування методу найменших квадратів до загальної лінійної багатофакторної моделі (3.1) передбачає наявність таких передумов:

1) кожне значення випадкової складової рівняння щ, і = 1,2,...,п, є випадковою величиною і математичне сподівання залишків щ до-рівнює нулю:

М(и) = 0;

2) компоненти вектора залишків некорельовані (лінійно неза-лежні) між собою і мають сталу дисперсію:

3) пояснюючі змінні (регресори, фактори моделі) некорельовані із залишками;

4) пояснюючі змінні некорельовані між собою.

9. Перевірка простої регресійної моделі на адекватність за f-критерый Фішера,

F - критерій Фішера використовують для порівняння дисперсій двох варіаційних рядів. Він обчислюється за формулою:

,

де - Велика дисперсія, - Менша дисперсія.

Якщо обчислене значення критерію F більше критичного для певного рівня значущості та відповідних чисел ступенів свободи для чисельника і знаменника, то дисперсії вважаються різними.

Число ступенів свободи чисельника визначається за формулою:

,

де - Число варіант для більшої дисперсії.

Число ступенів свободи знаменника визначається за формулою:

,

де - Число варіант для меншої дисперсії.

Перевірка простої регресійної моделі на адекватність

Для оцінки знайденої економетричної моделі на адекватність порівнюють розрахункове значення критерію Фішера із табличним.

Розрахункове значення критерію Фішера знаходиться за формулою:

,

де ,

,

n – число спостережень,

m – число включених у регресію факторів, які чинять суттєвий вплив на показник.

Для даної надійної ймовірності р (а=1-р рівня значущості) і числа ступенів вільності k₁=m, k₂=n-m-1 знаходиться табличне значення F(a, k₁, k₂). Отримане розрахункове значення порівнюється з табличним. При цьому, якщо F_роз> F(a, k₁, k₂), то з надійністю р = 1-а можна вважати, що розглянута економетрична модель адекватна вихідним даним. У протилежному випадку з надійністю р розглянуту лінійну регресію не можна вважати адекватною.

10. Коли відома величина , то цей результат можна бути використати для перевірки значущості елементів вектора та оцінювання довірчих інтервалів елементів цього вектора. Проте дисперсія невідома, а отже, потрібно розглянути методи її знаходження.

Для цього визначимо залишки:

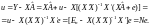(5.18)

Таким чином, залишки, які можна дістати на підставі експериментальних даних, записано у вигляді лінійних функцій від невідомих залишків . Тоді суму квадратів відхилень подамо у вигляді

(5.19)

де N— симетрична ідемпотентна матриця.

У цих перетвореннях ми виходили з того, що N є симетричною ідемпотентною матрицею, оскільки E_n — одинична матриця, а — симетрична розміром n  m.

Знайдемо математичне сподівання для обох частин рівняння (5.19) і застосуємо спочатку властивість, яка полягає в тому, що , де — слід матриці N, а далі — властивість комутативності добутку матриць відносно операцій обчислення сліду матриці.

З огляду на сказане маємо:

(5.20)

У цьому співвідношенні матриця має порядок , добуток дорівнює , а її слід дорівнює . Звідси

. (5.21)

Співвідношення (5.21) дає нам незміщену оцінку дисперсії залишків.

Нарешті, лишилося показати, що сума квадратів залишків розподілена незалежно від . Для цього знайдемо коваріацію залишків:

(5.22)

Оскільки і  є лінійні функції від нормально розподілених змінних, то вони також розподілені нормально і, як було показано, їх коваріації дорівнюють нулю.

Це дає нам змогу скористатися t-розподілом для перевірки гіпотез відносно істотності кожного з параметрів економетричної моделі

Перевірку гіпотези виконаємо згідно з t-критерієм:

, (5.23)

де — діагональний елемент матриці . Знаменник відношення (5.23) — називається стандартною помилкою оцінки параметра моделі.

Обчислене значення t-критерію порівнюється з табличним при вибраному рівні значущості і ступенях свободи. Якщо t факт >t табл, то відповідно оцінка параметра економетричної моделі є достовірною.

11. На основі t-критерію і стандартної помилки побудуємо довірчі інтервали для параметрів :

(5.24)

Приклад 5.5. Перевіримо гіпотези про значущість оцінок параметрів моделі (5.6)

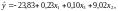
побудованої на основі вихідних даних, наведених у табл. 5.1.

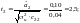
Якщо ступінь свободи = 10 – 4 = 6 і рівень значущості= 0,05, t табл = 1,945. Оскільки t₁факт >t табл, t₂ факт > t табл, то оцінки параметрів , характеризують істотний зв’язок цих незалежних змінних ( , ) із залежною; t₃ факт <t табл, що підтверджує нульову гіпотезу про неістот­ність впливу змінної на результативну ознаку .

Оцінка параметра може перебувати в таких межах:

12.

13. Оцінювання параметрів лінійної множинної регресії за МНК. Властивості оцінок параметрів.

Нехай ми маємо ряд спостережень за залежною змінною y = {y1, y2,…, yn} та за незалежними змінними або факторами:

Виходячи з цих спостережень, побудуємо лінійну вибіркову багатофакторну модель, яку при збереженні позначень, введених для простої лінійної регресії, можна записати у вигляді:

де у – залежна змінна; х1, х2,..., хр – незалежні змінні або фактори;

b1, b2,..., bр – невідомі параметри;

е – випадкова величина, або помилка.

Як і у випадку простої лінійної регресії, знайдемо невідомі параметри за методом найменших квадратів, тобто мінімізуючи суму квадратів відхилень:

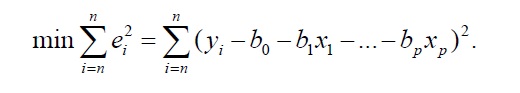
Для того, щоб знайти мінімум виразу, необхідно прирівняти до нуля частинні похідні. Ми отримаємо систему алгебраїчних рівнянь для знаходження коефіцієнтів.