
- •Методи розв’язування показникових рівнянь Передмова
- •Розділ 1. Загальні відомості про показникову функцію.
- •Означення та властивості степеневих виразів
- •Властивості степенів з дійсними показниками
- •Означення і властивості показникової функції
- •Основні властивості показникової функції
- •Розділ 2. Показникові рівняння
- •Рівняння, які розв’язуються застосуванням властивостей показникової функції Рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння, які розв’язуються методом групування і винесення спільного множника за дужки Показникове рівняння
- •Показникове рівняння вигляду
- •Показникові рівняння, які зводяться до алгебраїчних рівнянь заміною змінних Показникове рівняння вигляду
- •Показникове рівняння вигляду
- •Розділ 3. Системи показникових рівнянь
- •Показникові рівняння та нерівності.
- •Вправи для самостійної роботи
Показникове рівняння вигляду

де
 - деяка елементарна функція, а
- деяка елементарна функція, а
 - елементарна алгебраїчна функція,
розв’язується заміною
- елементарна алгебраїчна функція,
розв’язується заміною
 за допомогою якої рівняння зводиться
до алгебраїчного рівняння
за допомогою якої рівняння зводиться
до алгебраїчного рівняння

а)
Розв’язати рівняння
 .
.
Розв’язання. ОДЗ: .
Перетворимо задане рівняння до вигляду

Виконаємо
заміну
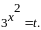 Тоді відносно
одержуємо рівняння
Тоді відносно
одержуємо рівняння
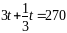 або
або

Т
=
-2;
=2.
Відповідь. = -2; =2.
Розділ 3. Системи показникових рівнянь
Системи показникових рівнянь в загальному випадку зводяться до систем алгебраїчних рівнянь застосуванням властивостей показникової функції, методів розв’язання показникових рівнянь, а також арифметичних дій над обома частинами рівнянь системи, введенням нових змінних тощо.
Розглянемо на прикладах застосування деяких з цих перетворень.
а)
Розв’язати систему рівнянь
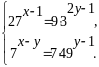
Розв’язання.
ОДЗ:

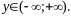
Приведемо кожне рівняння до однієї основи:

Одержали систему двох рівнянь вигляду (1.3), для якої рівносильною буде система алгебраїчних рівнянь

Відповідь:

б)
Розв’язати систему рівнянь
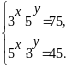
Розв’язання. ОДЗ:
Розкладемо праві частини рівнянь на множники

Перемножимо відповідно ліві і праві частини обох рівнянь:

Далі розділимо перше рівняння системи на друге:
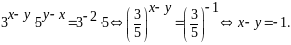
Таким
чином, одержали систему
 ,
розв’язуючи яку, маємо
,
розв’язуючи яку, маємо
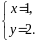
Відповідь:

в)
Розв’язати систему рівнянь
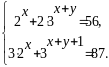
Розв’язання. ОДЗ:
Виконавши
заміни
 ,
одержимо систему
,
одержимо систему

яка
має розв’язок
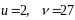 .
.
Тоді
для визначених
і
 маємо систему показникових рівнянь
маємо систему показникових рівнянь

звідки

Відповідь:
г)
Розв’язати систему рівнянь

Розв’язання.
ОДЗ:

Замінами
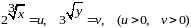 система зводиться до рівносильної
система зводиться до рівносильної

Додамо до лівої і правої частини другого рівняння відповідні частини першого, помноженого на 2, одержимо рівняння

Отже,
для визначення
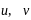 маємо дві системи:
маємо дві системи:
а)
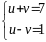 ,
з розв’язком
,
з розв’язком

б)
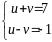 ,
з розв’язком
,
з розв’язком
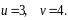
Тому для визначення і маємо також дві системи показникових рівнянь
а)

б)

Відповідь:
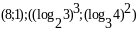 .
.
д)
Розв’язати систему рівнянь
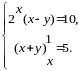
Розв’язання.
ОДЗ:

Зробимо
заміну
 ,
тоді система зводиться до рівносильної
,
тоді система зводиться до рівносильної
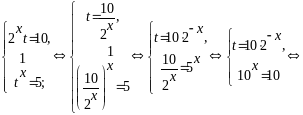

Перевірка показує, що знайдені розв’язки задовольняють дану систему.
Відповідь:
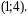
ж)
Розв’язати систему рівнянь
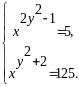
Розв’язання.
ОДЗ:

Піднесемо до куба обидві частини першого рівняння:

Прирівняємо ліві частини рівнянь:

Підставляючи
обидва значення
в будь-яке з рівнянь заданої системи,
одержимо
 .
.
Відповідь:

з)
Розв’язати систему рівнянь

Розв’язання.
ОДЗ:

Зробимо
заміну
 ,
тоді система зводиться до рівносильної
,
тоді система зводиться до рівносильної

Друге
рівняння одержаної системи –
степенево-показникове. Для його
розв’язання з чотирьох випадків,
залишимо лише два, оскільки
 ,
а саме:
,
а саме:
. Перевірка
 або
або
 ,
отже
= 1
,
отже
= 1
Отже,
 ,
оскільки
.
,
оскільки
.
Таким
чином, для знаходження
і
маємо тільки два значення:
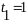 і
.
Отже:
і
.
Отже:
а)
при
маємо

б)
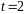 маємо
маємо

Відповідь:

Тест.
Показникові рівняння та нерівності.
1 Варіант
Яка з нерівностей є правильною:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
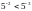 .
.
Яка з функцій є зростаючою:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
При яких значеннях
 правильна рівність:
правильна рівність:
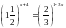
Розв’язати нерівність:

а)
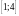 ;
б)
;
б)
 ;
в)
;
в)
 ;
г) інша відповідь.
;
г) інша відповідь.
Розв’язати рівняння:
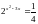
а) 1; б) 0; в) 2; г) 1;2.
Порівняти:
 і
і
 .
.
Розв’язати нерівність:

Розв’язати рівняння:

Знайти корені рівняння:
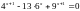
2 Варіант
Яка з нерівностей є правильною:
а)
 ;
б)
;
б)
 ;
в)
;
в)
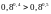 ;
г)
;
г)
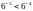 .
.
Яка з функцій є зростаючою:
а)
 ;
б)
;
б)
 ;
в)
;
в)
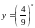 ;
г)
;
г)
 .
.
При яких значеннях правильна рівність:

а) 1; б) -1; в) 9; г) інша відповідь.
Розв’язати нерівність:

а)
 ;
б)
;
б)
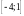 ;
в)
;
в)
 ;
г) інша відповідь.
;
г) інша відповідь.
Розв’язати рівняння:
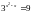
а) -1;2; б) -1; в) 2; г) 1.
Порівняти:
 і
і
 .
.
Розв’язати нерівність:

Розв’язати рівняння:
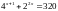
Знайти корені рівняння:

