
- •Методи розв’язування показникових рівнянь Передмова
- •Розділ 1. Загальні відомості про показникову функцію.
- •Означення та властивості степеневих виразів
- •Властивості степенів з дійсними показниками
- •Означення і властивості показникової функції
- •Основні властивості показникової функції
- •Розділ 2. Показникові рівняння
- •Рівняння, які розв’язуються застосуванням властивостей показникової функції Рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння вигляду
- •Показникові рівняння, які розв’язуються методом групування і винесення спільного множника за дужки Показникове рівняння
- •Показникове рівняння вигляду
- •Показникові рівняння, які зводяться до алгебраїчних рівнянь заміною змінних Показникове рівняння вигляду
- •Показникове рівняння вигляду
- •Розділ 3. Системи показникових рівнянь
- •Показникові рівняння та нерівності.
- •Вправи для самостійної роботи
Показникові рівняння вигляду
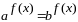 ,
,
в
якому
 - елементарна функція.
- елементарна функція.
Це
рівняння за допомогою ділення обох
частин на
 зводиться до рівняння вигляду
або
логарифмуванням за будь-якою основою
(наприклад,
)до
рівносильного рівняння
зводиться до рівняння вигляду
або
логарифмуванням за будь-якою основою
(наприклад,
)до
рівносильного рівняння
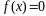 .
.
а)
Розв’язати рівняння
 .
.
Розв’язання. ОДЗ: .
Розділимо
обидві частини на
 :
:
 .
.
Це
рівняння вигляду
,
йому рівносильне рівняння вигляду
 з розв’язками
= -0,5
=1
з розв’язками
= -0,5
=1
Відповідь. = -0,5 =1.
б)
Розв’язати рівняння
 .
.
Розв’язання. ОДЗ: .
Приведемо
рівняння до вигляду
,
для чого представимо ліву частину у
вигляді
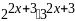 і розділимо обидві частини рівняння на
і розділимо обидві частини рівняння на
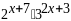 ,
тобто
,
тобто
 .
.
Розділивши
на
 ,
одержимо рівняння
,
одержимо рівняння
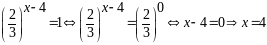 .
.
Відповідь. .
.
Показникові рівняння, які розв’язуються методом групування і винесення спільного множника за дужки Показникове рівняння
 ,
,
 -
дійсні коефіцієнти,
-
дійсні коефіцієнти,
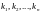 - цілі числа,
- цілі числа,
 -
алгебраїчна функція,
-
алгебраїчна функція,
 ,
винесенням за дужки множника
,
винесенням за дужки множника
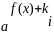 ,
де
,
де
 - найменший серед степенів в рівнянні,
зводиться до виду
- найменший серед степенів в рівнянні,
зводиться до виду
 або
або
 ,
,
 - стала величина
- стала величина
а)
Розв’язати рівняння

Розв’язання. ОДЗ: .
Винесемо
за дужки
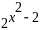 :
:
 ,
,
Звідки
 .
.
Відповідь.
= - ,
=
.
,
=
.
а)
Розв’язати рівняння

Розв’язання.
ОДЗ:
 .
.
Винесемо
за дужки
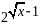 :
:

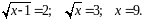
Відповідь.

Показникове рівняння вигляду

 (1.6)
(1.6)
де
 - дійсні коефіцієнти,
- дійсні коефіцієнти,
 - цілі числа,
- цілі числа,
 і
і
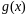 - алгебраїчні функції,
- алгебраїчні функції,
 винесення за дужки в лівій частині
множника
винесення за дужки в лівій частині
множника
 ,
де
,
де
 ,
- найменший з показників степеня лівої
частини, а в правій – множника
,
- найменший з показників степеня лівої
частини, а в правій – множника
 ,
де
,
де
 - найменший з показників правої частини,
зводиться до вигляду
- найменший з показників правої частини,
зводиться до вигляду

(
і
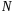 - сталі величини), тобто до рівняння
- сталі величини), тобто до рівняння
 .
.
а)
Розв’язати рівняння
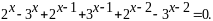
Розв’язання. ОДЗ: .
Згрупуємо члени рівняння з однаковими основами:

Винесемо
в лівій частині за дужки множник
 ,
а в правій
,
а в правій
 :
:

Розділимо
обидві частини на
 :
:

Відповідь.

б)
Розв’язати рівняння

Розв’язання. ОДЗ: .
Зауваживши,
що
 ,
приведемо рівняння до вигляду (1.6):
,
приведемо рівняння до вигляду (1.6):



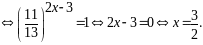
Відповідь.

Показникові рівняння, які зводяться до алгебраїчних рівнянь заміною змінних Показникове рівняння вигляду

 -
дійсні коефіцієнти, діленням на
-
дійсні коефіцієнти, діленням на
 зводиться до виду
зводиться до виду
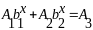 .
(1.7)
.
(1.7)
Рівняння
(1.7) в частинному випадку, коли
 (
( - ціле число), заміною
- ціле число), заміною
 і відповідно
і відповідно
 зводиться до раціонального рівняння.
зводиться до раціонального рівняння.

а)
Розв’язати рівняння

Розв’язання. ОДЗ: .
Розділимо
обидві частини рівняння на
 :
:

Оскільки
 ,
то, виконавши заміну
,
то, виконавши заміну
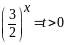
 одержимо
рівняння
одержимо
рівняння
 з
розв’язками
з
розв’язками
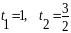 .
.
Отже, для визначених маємо два рівняння:
 і
і

Відповідь.

а)
Розв’язати рівняння

Розв’язання. ОДЗ: .
Запишемо дане рівняння у вигляді

Поділивши
обидві частини рівняння на
 отримаємо
отримаємо
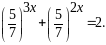
Зробимо
заміну
 тоді відносно
тоді відносно
 рівняння зводиться до вигляду
рівняння зводиться до вигляду
 ,
або
,
або
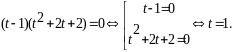
Квадратне
рівняння не має дійсних коренів, оскільки
дискримінант
 тому існує єдиний корінь
тому існує єдиний корінь
 .
.
Таким чином, для визначених маємо одне рівняння
 звідки
звідки
 .
.
Відповідь.

а)
Розв’язати рівняння

Розв’язання. ОДЗ: .
Розділимо
обидві частини рівняння на
 :
:

Впевнившись,
що
 є розв’язком одержаного рівняння,
покажемо, що воно не має інших розв’язків.
є розв’язком одержаного рівняння,
покажемо, що воно не має інших розв’язків.
Оскільки
 і
і
 ,
то функції
,
то функції
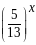 і
і
 монотонно спадні, а отже і їх сума (ліва
частина рівняння також монотонно спадна
функція, яка може прийняти будь-яке
додатне значення лише в одній точці.
Оскільки ми вже визначили одну таку
точку
,
то інших значень
,
які задовольняють рівнянню не існує.
монотонно спадні, а отже і їх сума (ліва
частина рівняння також монотонно спадна
функція, яка може прийняти будь-яке
додатне значення лише в одній точці.
Оскільки ми вже визначили одну таку
точку
,
то інших значень
,
які задовольняють рівнянню не існує.
Відповідь.
