МІНІСТЕРСТВО ОСВІТИ НАУКИ МОЛОДІ ТА СПОРТУ УКРАЇНИ

БОГУСЛАВСЬКИЙ ГУМАНІТАРНИЙ КОЛЕДЖ ІМЕНІ І.С. НЕЧУЯ – ЛЕВИЦЬКОГО

Методи розв’язування показникових рівнянь та їх систем

Навчальний посібник

Богуслав 2012

Методи розв’язування показникових рівнянь. Посібник для студентів 1,2 курсів, учнів старших класів. / Укл. Л.І.Федорченко. Богуслав, 2012. – -- с.

Обговорено і схвалено на засіданні циклової комісії викладачів природничо-математичних дисциплін Богуславського гуманітарного коледжу імені І.С.Нечуя-Левицького

(Протокол №__ від __.__. 2012 р.)

Укладач:

Федорченко Любов Іванівна – викладач фізико-математичних дисциплін Богуславського гуманітарного коледжу ім.І.С.Нечуя-Левицького, спеціаліст вищої кваліфікаційної категорії

Зміст

1. Передмова…………………………………………………………………..

2. Розділ 1. Загальні відомості про показникову функцію……………..

3. Розділ 2. Показникові рівняння…………………………………………

4. Розділ 3. Системи показникових рівнянь………………………………

5. Тест. Показникові рівняння та нерівності)…………………………….

6. Вправи для самостійного розв’язування………………………………

7. Відповіді…………………………………………………………………….

8. Список використаної літератури……………………………………..

Методи розв’язування показникових рівнянь Передмова

Глибокі і тривалі знання з математики можна одержати, лише засвоївши основний теоретичний матеріал і розв’язавши достатню кількість вправ щодо його застосування. Важливою передумовою розв’язання задачі є чітка її математична підготовка, обґрунтування і повнота її розв’язання, підтвердження правильності відповіді. У посібникові пропонуються методи розв’язання основних типів задач розділу «Показникові рівняння». Застосування кожного з цих методів ілюструється необхідною кількістю прикладів. Як довідковий матеріал наведені основні властивості степенів та показникової функції. Пропонуються вправи для самостійного розв’язування, до яких даються відповіді. При підготовці не варто обмежуватися розв’язуванням лише цих вправ.

Розділ 1. Загальні відомості про показникову функцію.

Для розв’язування показникових рівнянь необхідно знати загальні відомості та основні властивості степеневих виразів, показникової функції.

Означення та властивості степеневих виразів

Степенем числа називається добуток 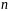множників, кожен з яких дорівнює :

де - натуральне число.

де ,

, за умови, що , бо вираз не існує.

,

Якщо , а - натуральні числа.

Приклад

А)

Б)

В)

Г)

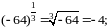
Д) не має місця.

Властивості степенів з дійсними показниками

1. Добуток степенів з однаковими основами дорівнює степеню з тією ж основою та показником, який дорівнює сумі показників степенів, що перемножуються.

2. Частка від ділення степенів з однаковими основами дорівнює степеню з тією ж основою та показником, як дорівнює різниці показників діленого і дільника:

3. Степінь степеня дорівнює степеню з тією ж основою і показником, який дорівнює добутку показників наданих степенів:

4. Степінь добутку двох чисел дорівнює добутку таких саме степенів співмножників:

5. Степінь дробу дорівнює частці від ділення таких самих степенів чисельника і знаменника, а саме:

Зауваження. Властивості, які обернені властивостям 4-8 також вірні.

6. Значення степеня додатного числа з додатним показником не зміниться, якщо чисельник і знаменник показника помножити на будь-яке натуральне число:

7. для будь-якого дійсного числа .

8. Якщо і , то .

Якщо і , то .

9. Якщо і , то .

Якщо і , то .

10. 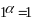для будь-якого .

Означення і властивості показникової функції

Показниковою функцією незалежної змінної 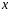називається функція виду , де - дійсне число _.

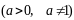Якщо , то функція визначена лише для цілих або рівних дробу , де і - цілі числа і - непарне число.

Якщо , то визначено при . Якщо , то функція визначена при всіх дійсних значеннях .

Зауваження. Якщо , а саме , то функція є сталою величиною.

Основні властивості показникової функції

1. Функція визначена для всіх значень .

2. Область значень функції є множина всіх додатних чисел, а саме .

3. Функція є однозначною, тобто одному значенню відповідає одне значення , і навпаки.

4. При функція всюди зростає, а при функція спадає.

Приклад

а) Спростити вираз .

.

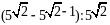б) Обчислити: .

.

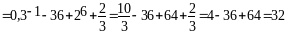в) Спростити вираз, виконавши дії:

.

.

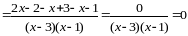г) Розкласти на множники:

.

д) Знайти значення виразу:

.
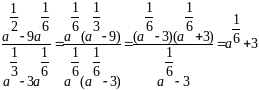