МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

в ысшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ЭНРГЕТИЧЕСКИЙ ИНСТИТУТ

_____________________________________________________________________________________________

Кафедра

Атомных и Тепловых

Электрических Станций

Лабораторная работа № 1

“Измерение коэффициента теплопроводности методом монотонного режима”

по дисциплине “Тепломассообмен в энергетическом оборудовании”

Выполнила студентка гр. 5011	Кабанова М.А.
Проверил	Раков Ю.Я.

Томск 2014

Содержание:

Y

Введение 3

1. Элементы исследования 3

2. Теоретическое обоснование метода измерения теплопроводности в монотонном режиме 4

3. Вывод формулы для измерительной ячейки 6

4. Конструкция измерителя 9

5. Описание принципиальной схемы измерителя. 9

5.1. Определение тепловой проводимости тепломера. 10

5.2. Определение теплового сопротивления контакта 11

5.3. Уточнение 11

5.4. Расчет погрешностей определения и 12

6 Обработка результатов эксперимента 13

Вывод: 15

Введение

Цель работы заключается:

• в закреплении лекционного материала по теоретическим основам метода монотонного режима для измерения коэффициента теплопроводности в практической работе о промышленным измерителем ИТ- -400;

• в изучении принципиальной конструкции измерителя ИТ- -400, методики его градуировки, поверки и проведения измерений;

• в приобретении навыков экспериментального определения образца, обработки результатов измерения и анализа полученных данных.

1. Элементы исследования

Элементы исследования при проведении лабораторных работ включает:

• получение экспериментальной зависимости новых материалов от температуры;

• построение графической зависимости от температуры 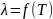, подбор и определение эмпирической формулы этой зависимости на основе метода наименьших квадратов;

• проведение оценок погрешности результатов измерения и анализ полученных результатов.

2. Теоретическое обоснование метода измерения теплопроводности в монотонном режиме

Основные закономерности монотонного режима

Рассмотрим неограниченную пластину образец 1 толщиной 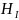на плохопроводящего материала, которая находится в идеальном тепловом контакте с металлической пластиной 2, имеющей толщину 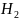(рис. 1, а). На лицевую грань пластины 1 действует постоянный тепловой потом плотности , тыльная сторона пластины 2адиабатизирована и температурное поле в ней остается практически равномерным на всех стадиях процесса.

Распределение температуры в пластине 1 описывается одномерным нестационарным уравнением теплопроводности (1) и краевыми условиями (2)÷(4):

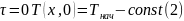
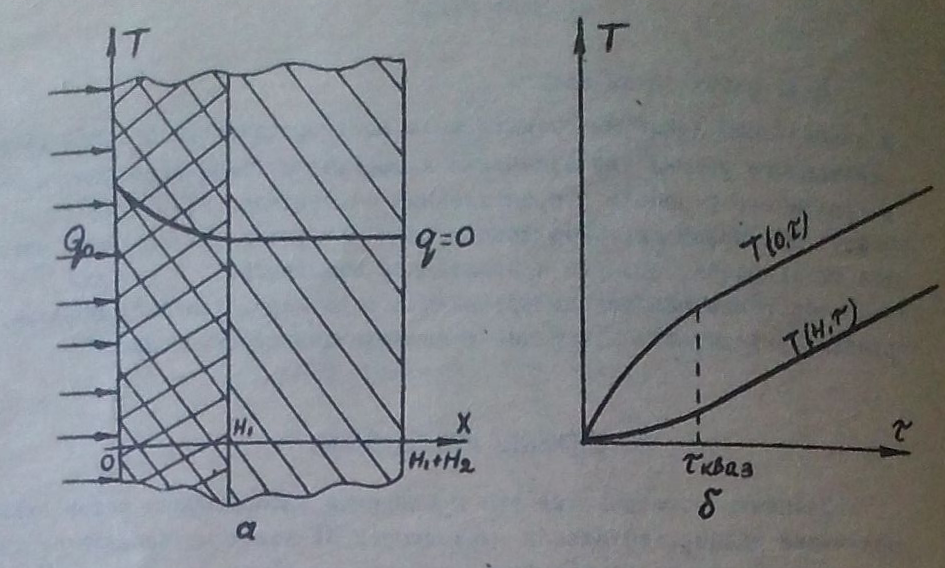
Рис. 1. Двухслойная система - металлическое ядро 2 и теплоизоляционная оболочка 1 при нагреве постоянным потоком: а – распределение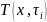 ;б – зависимости и .

При достижении определенного времени от начала процесса нагрева , все слои системы повышают температуру с одинаковой постоянной скоростью (квазистационарная стадия процесса) и температурное поле в пластине 1перестаетзависит от начальных условий (рис.1б). В этом случае вышеприведенная математическая постановка задачи для определения температурного поля в пластине упрощается и имеет вид:

Для решения системы (5)÷(7) проинтегрируем дважды уравнение (5), получим

Используя граничные условия (6) и (7) найдем значения константы :

Применяя формулу (10) к точке с координатой 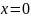и заменяя скорость нагрева выражением из интегрального баланса

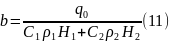
получим

Из формулы (12) следует расчетные соотношения для определения теплового сопротивления образца и его теплопроводности соответственно:

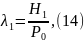
Где

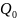- тепловой поток, поступающий в образец;

- площадь сечения пластины, м²;

- полная теплоемкость пластины 1;

- полная теплоемкость пластины 2, Дж/К.

Если между пластинами 1 и 2 имеет место неидеальный тепловой контакт и известна температура пластины 2, то в формуле (13) необходимо учитывать тепловое сопротивление контакта и для расчета теплового сопротивления образца использовать выражение

Методика расчета теплового потока зависит от вида измерительной ячейки.