6. Прямая геодезическая задача.

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние S_ABот неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей. В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

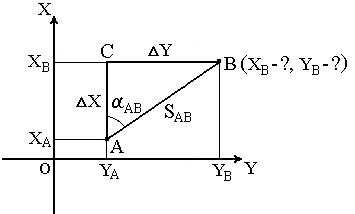
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А( X_A, Y_A ), S_AB и α_AB.

Найти: точку В( X_B, Y_B ).

Непосредственно из рисунка имеем:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB ;

ΔY = S_AB · sin α_AB .

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB ;

ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

 X_B = X_A + ΔX  ;

 Y_B = Y_A + ΔY  .

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

7. Обратная геодезическая задача.

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB (рис.24).

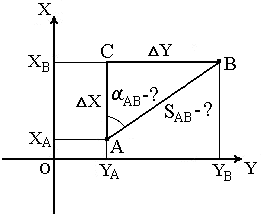
Рис. 24. Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Величину угла r_AB определем из отношения

ΔY	= tg rAB
ΔX

 .

 

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Расстояние S_AB можно определить также по формуле

.

9. Схема геометрических осей теодолита. Поверки теодолита.

ZZ1 – вертикальная ось вращения теодолита; UU1 – ось цилиндрического уровня на алидаде горизонтального круга; HH1 – горизонтальная ось вращения зрительной трубы;

WW1 – визирная ось зрительной трубы. Должны выполняться следующие геометрические условия:

UU1ZZ1; WW1HH1; HH1ZZ1.

Поверки:

1. Ось цилиндрического уровня на алидаде горизонтального круга должна быть перпендикулярна к вертикальной оси вращения теодолита (UU1ZZ1)

2. Горизонтальная нить сетки нитей должна быть перпендикулярна к вертикальной оси вращения теодолита

3. Визирная ось зрительной трубы должна быть перпендикулярна к горизонтальной оси вращения трубы (WW1HH1)

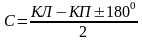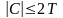Для выполнения поверки наводят зрительную трубу на удаленную точку вблизи горизонта и при «круге лево» берут отсчет по горизонтальному кругу - КЛ. Затем переводят трубу через зенит, снова визируют на точку при положении «круг право» и берут отсчет КП. Коллимационную ошибку С вычисляют по формуле: . Если , где Т – точность теодолита, то условие выполнено. При нарушении этого условия выполняют юстировку.

4. Горизонтальная ось вращения зрительной трубы должна быть перпендикулярна к вертикальной оси теодолита (HH1ZZ1

5 Место нуля вертикального круга должно быть постоянным и близким к нулю

Место нуля (МО) – вычисленный отсчет по вертикальному кругу при горизонтальном положении зрительной трубы.